БИЛЕТ 31 оптические свойства
Оптические свойства гиперболы: фокальные радиусы произвольной точки M0 гиперболы составляют равные углы с касательной к эллипсу в точке M0.
Оптическое свойство Эллипса : Касательная эллипса образует в точке касания равные острые углы с фокальными радиусами.
Оптическое свойство ПАРАБОЛЫ:
Угол образуемый радиус вектором r=FM0 и касательной к параболе равен углу образуемому касательной с фокальной осью параболы.
БиЛЕТ 32
Общее уравнение кривой второго порядка:  . Любая кривая второго порядка описывается таким уравнением и наоборот. Все кривые второго порядка могут быть разделены на две группы: невырожденные (эллипс, гипербола, параболы) и вырожденные. Пример вырожденной кривой: . Любая кривая второго порядка описывается таким уравнением и наоборот. Все кривые второго порядка могут быть разделены на две группы: невырожденные (эллипс, гипербола, параболы) и вырожденные. Пример вырожденной кривой: 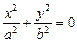 . .
Билет 33
Цилиндрические
Цилиндрические поверхности – поверхности, образованные прямыми, параллельными некоторой фиксированной прямой. Эта прямая называется осью. Прямые, с помощью которых образована цилиндрическая поверхность – образующими. Кривая, лежащая на цилиндрической поверхности и проходящая через все образующие называется направляющей.
Если ось цилиндрической поверхности параллельна, к примеру, Ox, то уравнение этой поверхности не будет содержать переменной x.
 - уравнение кругового цилиндра, - уравнение кругового цилиндра,  - уравнение эллиптического цилиндра, - уравнение эллиптического цилиндра,  - уравнение гиперболического цилиндра, - уравнение гиперболического цилиндра,  - уравнение параболического цилиндра. - уравнение параболического цилиндра.
Билет 34
Поверхности вращения
Поверхность вращения – это поверхность, составленная из окружностей, центры которых лежат на одной прямой, а сами окружности лежат в плоскостях, перпендикулярных этой прямой.
Возьмём эллипс, описываемый уравнением  , и начнём вращать его вокруг большей оси. Тогда точка , и начнём вращать его вокруг большей оси. Тогда точка  будет вращаться по окружности, описываемой системой уравнений будет вращаться по окружности, описываемой системой уравнений  . Подставим эти значения в уравнение эллипса: . Подставим эти значения в уравнение эллипса:  - уравнение эллипсоида вращения . Начнём теперь «прижимать» все точки эллипса к плоскости xOz. В результате точка - уравнение эллипсоида вращения . Начнём теперь «прижимать» все точки эллипса к плоскости xOz. В результате точка  будет «вращаться» не по окружности, а по эллипсу. В итоге мы получим уравнение эллипсоида: будет «вращаться» не по окружности, а по эллипсу. В итоге мы получим уравнение эллипсоида:  . .
БИЛЕТ 35
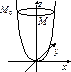
 Возьмём теперь параболу, описываемую уравнением Возьмём теперь параболу, описываемую уравнением  , и начнём её вращать вокруг оси Oz. В результате точка , и начнём её вращать вокруг оси Oz. В результате точка  будет вращаться по окружности, описываемой системой уравнений будет вращаться по окружности, описываемой системой уравнений  . Подставив эти выражения в уравнение параболы, получим: . Подставив эти выражения в уравнение параболы, получим:  - уравнение параболоида вращения. Если мы будем «сжимать» этот параболоид к плоскости xOz, то точка - уравнение параболоида вращения. Если мы будем «сжимать» этот параболоид к плоскости xOz, то точка  будет двигаться по эллипсу и уравнение параболоида примет вид будет двигаться по эллипсу и уравнение параболоида примет вид  . .
 Исследуем, наконец, гиперболу, описываемую уравнением Исследуем, наконец, гиперболу, описываемую уравнением  . Если мы начнём вращать её вокруг оси z, то точка . Если мы начнём вращать её вокруг оси z, то точка  будет вращаться по окружности, описываемой системой уравнений будет вращаться по окружности, описываемой системой уравнений  . Подставив эти значения в уравнение гиперболы, получим: . Подставив эти значения в уравнение гиперболы, получим:  - уравнение однополостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение однополостного гиперболоида: - уравнение однополостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение однополостного гиперболоида:  . .
Если же мы начнём вращать гиперболу вокруг оси Ox, то точка  будет вращаться по окружности, описываемой системой уравнений будет вращаться по окружности, описываемой системой уравнений  . Подставив эти значения в уравнение гиперболы, получим: . Подставив эти значения в уравнение гиперболы, получим:  - уравнение двуполостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение двуполостного гиперболоида: - уравнение двуполостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение двуполостного гиперболоида: 
 Теперь возьмём прямую, описываемую уравнением Теперь возьмём прямую, описываемую уравнением  и начнём вращать её вокруг оси Oz. Тогда точка и начнём вращать её вокруг оси Oz. Тогда точка  опять будет вращаться по окружности, описываемой системой уравнений опять будет вращаться по окружности, описываемой системой уравнений  . Подставив эти выражения в уравнение прямой, получим: . Подставив эти выражения в уравнение прямой, получим:  или или  - уравнение конуса. - уравнение конуса.
Поверхность, описываемая уравнением  , называется гиперболическим параболоидом. Если расположить гиперболический параболоид так, как показано на рисунке, то сечение его плоскостью, параллельной xOy будет представлять собой гиперболу, причём если сечь плоскостью, параллельной xOy, сначала ниже самой плоскости xOy, сечение будет представлять собой одну гиперболу, то сечение плоскостью выше xOy – ей сопряжённую. Сечение плоскостью, параллельной zOy и xOz представляет собой параболу. Таким образом, гиперболический параболоид – это поверхность, которую образует одна парабола, двигаясь по другой параболе, расположенной относительно первой так, как показано на рисунке. , называется гиперболическим параболоидом. Если расположить гиперболический параболоид так, как показано на рисунке, то сечение его плоскостью, параллельной xOy будет представлять собой гиперболу, причём если сечь плоскостью, параллельной xOy, сначала ниже самой плоскости xOy, сечение будет представлять собой одну гиперболу, то сечение плоскостью выше xOy – ей сопряжённую. Сечение плоскостью, параллельной zOy и xOz представляет собой параболу. Таким образом, гиперболический параболоид – это поверхность, которую образует одна парабола, двигаясь по другой параболе, расположенной относительно первой так, как показано на рисунке.

Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . Любая кривая второго порядка описывается таким уравнением и наоборот. Все кривые второго порядка могут быть разделены на две группы: невырожденные (эллипс, гипербола, параболы) и вырожденные. Пример вырожденной кривой:
. Любая кривая второго порядка описывается таким уравнением и наоборот. Все кривые второго порядка могут быть разделены на две группы: невырожденные (эллипс, гипербола, параболы) и вырожденные. Пример вырожденной кривой: 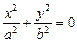 .
. - уравнение кругового цилиндра,
- уравнение кругового цилиндра,  - уравнение эллиптического цилиндра,
- уравнение эллиптического цилиндра,  - уравнение гиперболического цилиндра,
- уравнение гиперболического цилиндра,  - уравнение параболического цилиндра.
- уравнение параболического цилиндра. , и начнём вращать его вокруг большей оси. Тогда точка
, и начнём вращать его вокруг большей оси. Тогда точка  будет вращаться по окружности, описываемой системой уравнений
будет вращаться по окружности, описываемой системой уравнений  . Подставим эти значения в уравнение эллипса:
. Подставим эти значения в уравнение эллипса:  - уравнение эллипсоида вращения . Начнём теперь «прижимать» все точки эллипса к плоскости xOz. В результате точка
- уравнение эллипсоида вращения . Начнём теперь «прижимать» все точки эллипса к плоскости xOz. В результате точка  будет «вращаться» не по окружности, а по эллипсу. В итоге мы получим уравнение эллипсоида:
будет «вращаться» не по окружности, а по эллипсу. В итоге мы получим уравнение эллипсоида:  .
.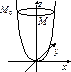
 Возьмём теперь параболу, описываемую уравнением
Возьмём теперь параболу, описываемую уравнением  , и начнём её вращать вокруг оси Oz. В результате точка
, и начнём её вращать вокруг оси Oz. В результате точка  будет вращаться по окружности, описываемой системой уравнений
будет вращаться по окружности, описываемой системой уравнений  . Подставив эти выражения в уравнение параболы, получим:
. Подставив эти выражения в уравнение параболы, получим:  - уравнение параболоида вращения. Если мы будем «сжимать» этот параболоид к плоскости xOz, то точка
- уравнение параболоида вращения. Если мы будем «сжимать» этот параболоид к плоскости xOz, то точка  .
. Исследуем, наконец, гиперболу, описываемую уравнением
Исследуем, наконец, гиперболу, описываемую уравнением  . Если мы начнём вращать её вокруг оси z, то точка
. Если мы начнём вращать её вокруг оси z, то точка  - уравнение однополостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение однополостного гиперболоида:
- уравнение однополостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение однополостного гиперболоида:  .
. будет вращаться по окружности, описываемой системой уравнений
будет вращаться по окружности, описываемой системой уравнений  . Подставив эти значения в уравнение гиперболы, получим:
. Подставив эти значения в уравнение гиперболы, получим:  - уравнение двуполостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение двуполостного гиперболоида:
- уравнение двуполостного гиперболоида вращения. «Сжимая» его к плоскости xOz, получим уравнение двуполостного гиперболоида: 
 Теперь возьмём прямую, описываемую уравнением
Теперь возьмём прямую, описываемую уравнением  и начнём вращать её вокруг оси Oz. Тогда точка
и начнём вращать её вокруг оси Oz. Тогда точка  или
или  - уравнение конуса.
- уравнение конуса. , называется гиперболическим параболоидом. Если расположить гиперболический параболоид так, как показано на рисунке, то сечение его плоскостью, параллельной xOy будет представлять собой гиперболу, причём если сечь плоскостью, параллельной xOy, сначала ниже самой плоскости xOy, сечение будет представлять собой одну гиперболу, то сечение плоскостью выше xOy – ей сопряжённую. Сечение плоскостью, параллельной zOy и xOz представляет собой параболу. Таким образом, гиперболический параболоид – это поверхность, которую образует одна парабола, двигаясь по другой параболе, расположенной относительно первой так, как показано на рисунке.
, называется гиперболическим параболоидом. Если расположить гиперболический параболоид так, как показано на рисунке, то сечение его плоскостью, параллельной xOy будет представлять собой гиперболу, причём если сечь плоскостью, параллельной xOy, сначала ниже самой плоскости xOy, сечение будет представлять собой одну гиперболу, то сечение плоскостью выше xOy – ей сопряжённую. Сечение плоскостью, параллельной zOy и xOz представляет собой параболу. Таким образом, гиперболический параболоид – это поверхность, которую образует одна парабола, двигаясь по другой параболе, расположенной относительно первой так, как показано на рисунке.