
|
|
Условие параллельности двух плоскостей.Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
Условие перпендикулярности плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, Таким образом, Билет 24 Прямая в пространстве
Общее уравнение прямой в пространстве Составим уравнение прямой, проходящей через точку
Чтобы составит уравнение прямой, проходящей через две данные точки Если взять называется параметрическими уравнениями прямой.
Билет 26 Прямую можно также задать как множество точек, общих для двух плоскостей системой уравнений вида Ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Расстояние между двумя скрещивающимися прямыми Пусть Пусть даны канонические уравнения двух прямых Чтобы две прямые были параллельны необходимо и достаточно, чтобы направляющие векторы этих прямых были коллинеарны, т.е. их соответствующие координаты были пропорциональны. Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.
Записав через координаты, получим
БИЛЕТ 27 Окружность – геометрическое место точек, расстояния от которых до одной фиксированной (центра) равны.
1. Если 2. Эллипс имеет две оси симметрии (Ox и Oy) и центр симметрии ( 3. Эллипс – непрерывная кривая. 4. Ограниченная кривая, 5. Гладкая кривая (во всех точках имеет касательную). 6. Уравнение касательной для эллипса: 7. Верхняя половина эллипса выпукла вверх, нижняя – вниз. 8. 9. 10. 11.
Билет 28
Гипербола – геометрическое место точек, абсолютные величины разности расстояний от которых до двух фиксированных (фокусов) равны. Введём систему координат так, как показано на рисунке. Здесь, так же, как и у эллипса, 1. Гипербола имеет две оси симметрии (Ox и Oy) и центр симметрии ( 2. Гипербола – гладкая кривая. 3. Уравнение касательной для гиперболы: 4. Гипербола, задающаяся уравнением 5. 6. 7. Эксцентриситет гиперболы 8. 9. Билет 29
Парабола имеет ось симметрии (Ox).
Эксцентриситет параболы
Билет 30
Директориальные свойства Парабола есть множество всех точек, равноудаленных от фокуса и директрисы y^2 = 2px . это свойство параболы называется директориальным свойством параболы и используется как определение.
Эллипс: Расстояние точки эллипса М(x,y) до левой директрисы x=-a/e
Гипербола: r1/d1=r2/d2=e если М(x,y,) есть произвольная точка гиперболы то ее расстояние до правой директрисы есть d2=x-(a/e) r2=ex-a , а до левой d1=x+(a/e) r1=ex+a

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 и
и 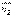 параллельны, а значит
параллельны, а значит  .
. или
или 
 или
или 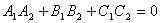 .
. .
. параллельно вектору
параллельно вектору  . Пусть
. Пусть  принадлежит этой прямой. Это значит, что
принадлежит этой прямой. Это значит, что  , т.е.
, т.е.  - канонические уравнения прямой.
- канонические уравнения прямой. Билет25
Билет25 и
и  , достаточно взять
, достаточно взять  . Тогда
. Тогда  - канонические уравнения этой прямой.
- канонические уравнения этой прямой. , то система уравнений
, то система уравнений 
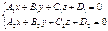 , где оба уравнения представляют собой уравнения пересекающихся плоскостей. Чтобы перейти от этого вида к каноническому, достаточно найти одну точку, удовлетворяющую этому неравенству и взять её как точку
, где оба уравнения представляют собой уравнения пересекающихся плоскостей. Чтобы перейти от этого вида к каноническому, достаточно найти одну точку, удовлетворяющую этому неравенству и взять её как точку  и положить
и положить  .
. и
и 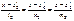 - уравнения прямых
- уравнения прямых  и
и  . Тогда
. Тогда  и
и  - направляющие векторы этих прямых. Поместим
- направляющие векторы этих прямых. Поместим  на прямую
на прямую  совместим с началом
совместим с началом  . На трёх векторах
. На трёх векторах  и
и  построим параллелепипед. Расстояние между прямыми будет равно высоте полученного параллелепипеда:
построим параллелепипед. Расстояние между прямыми будет равно высоте полученного параллелепипеда:  .
.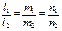 , то
, то  , иначе
, иначе 





 или
или  .
. Эллипс – геометрическое место точек, сумма расстояний от которых до двух фиксированных (полюсов) равны.
Эллипс – геометрическое место точек, сумма расстояний от которых до двух фиксированных (полюсов) равны. . Введём систему координат так, как показано на рисунке. Здесь
. Введём систему координат так, как показано на рисунке. Здесь  ,
,  ,
, 
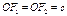 . Такую систему координат называют канонической. Тогда
. Такую систему координат называют канонической. Тогда  ,
,  . Возьмём любую точку
. Возьмём любую точку  , принадлежащую нашему эллипсу. Тогда
, принадлежащую нашему эллипсу. Тогда  Преобразуем это выражение:
Преобразуем это выражение:  ,
, 
 ,
,  . Сложим теперь его с исходным:
. Сложим теперь его с исходным:  ,
,  ,
,  ,
,  ,
,  . Обозначив
. Обозначив  , получим каноническое уравнение эллипса:
, получим каноническое уравнение эллипса:  . Здесь a и b равны соответственно горизонтальной и вертикальной полуосям эллипса. Отсюда уравнение эллипса в явном виде:
. Здесь a и b равны соответственно горизонтальной и вертикальной полуосям эллипса. Отсюда уравнение эллипса в явном виде:  .
. , то уравнение эллипса представляет собой окружность.
, то уравнение эллипса представляет собой окружность. ).
). ,
,  .
. .
. и
и  называются фокальными радиусами.
называются фокальными радиусами. - эксцентриситет эллипса,
- эксцентриситет эллипса,  .
. ,
,  .
.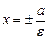 - директрисы эллипса.
- директрисы эллипса. , т.е.
, т.е.  ,
,  . Такая система координат называется канонической. Условие гиперболы записывается так:
. Такая система координат называется канонической. Условие гиперболы записывается так:  или
или  . Избавившись от иррациональности (см. вывод уравнение эллипса выше), получим:
. Избавившись от иррациональности (см. вывод уравнение эллипса выше), получим: 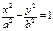 , где
, где  . Уравнение гиперболы в явном виде:
. Уравнение гиперболы в явном виде:  .
. ).
). .
. , называется сопряжённой для исследуемой гиперболы.
, называется сопряжённой для исследуемой гиперболы. - асимптоты гиперболы.
- асимптоты гиперболы. ,
,  .
. ,
,  .
. - директрисы гиперболы.
- директрисы гиперболы. Парабола – геометрическое место точек, расстояния от которых до одной фиксированной и до фиксированной прямой, называемой директрисой, равны.
Парабола – геометрическое место точек, расстояния от которых до одной фиксированной и до фиксированной прямой, называемой директрисой, равны. Введём систему координат так, как показано на рисунке. Здесь
Введём систему координат так, как показано на рисунке. Здесь 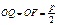 . Такая система координат называется канонической. Тогда условие параболы запишется так:
. Такая система координат называется канонической. Тогда условие параболы запишется так:  . Избавившись от иррациональности, получим:
. Избавившись от иррациональности, получим:  - каноническое уравнение параболы. Уравнение параболы в явном виде:
- каноническое уравнение параболы. Уравнение параболы в явном виде:  .
. ,
,  .
. .
.