
|
|
Геометрические свойства смешанного произведения
2. Смешанное произведение
Докажем первое свойство. Найдем по определению смешанное произведение: , где
Знак смешанного произведения определяется знаком косинуса угла Докажем второе свойство. Равенство возможно в трех случаях: Критерий компланарности трёх векторов: Для того чтобы векторы В самом деле, это означает, что объём параллелепипеда, построенного на этих векторах после приведения их к общему началу, будет равен нулю, а это возможно только когда все три вектора лежат в одной или параллельных плоскостях, т.е. компланарны.
Билет11 Тройно́е ве́кторное произведе́ние (другое название: двойное векторное произведение) Двойным векторным произведением векторов
Свойства. Формула Лагранжа Для двойного векторного произведения справедлива формула Лагранжа,
Билет 12
Прямая на плоскости Составим уравнение прямой, проходящей через данную точку Запишем условие принадлежности точки Ненулевой вектор, перпендикулярной данной прямой называют нормальным вектором прямой. Приняв
Билет 13
Запишем условие принадлежности точки Ненулевой вектор, параллельный данной прямой, называют направляющим вектором этой прямой. Уравнение прямой, проходящей через две данные точки Если мы преобразуем канонические уравнения прямой следующим образом:
Угол между прямыми Это угол, на который нужно повернуть одну прямую до совмещения её с другой прямой. 1. Пусть 2. Пусть 3. Пусть Билет 14 Полные и неполные уравнения прямой Общее уравнение прямой Полное уравнение прямой можно привести к уравнению прямой в отрезках: обозначим
Билет 15 Неполные уравнения прямой: 1. 2. 3. 4. 5.
Билет 16 Нормальное уравнения прямой это уравнение прямой Нормальное уравнение прямой получается из полного следующим образом:
Вывод нормального уравнения прямой: Введём сразу две системы координат – полярную и цилиндрическую так, чтобы их начала совпадали, и ось полярной системы совпадала с осью Ox цилиндрической. Тогда выражение
Приведём общее уравнение прямой к нормальному виду ( Чтобы привести общее уравнение прямой к нормальному виду нужно обе части равенства
Геометрический смысл коэффициентов A B C в обоих случаях - расстояние от нач. координат до точки принадлежащей плоскости (прямой) по осям соответственно Ox Oy & Oz. Отклонением точки от прямой называется расстояние от этой точки до прямой, взятое со знаком «+», если эта точка и начало координат располагаются по одну сторону от прямой и «–» - если по разные стороны, т.е. отклонение равно С помощью нормальных уравнений прямой можно составлять уравнения биссектрис, образованных двумя прямыми: Пусть
Пусть прямые
Билет 17 Обозначим через φ величину угла между прямыми
и, следовательно,
Записав через координаты, получим
Если прямые
то нормальные векторы этих прямых могут быть
Из последнего выражения следует, что если
Отсюда получаем Если Следовательно, необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами 4. Условия параллельности двух прямых: а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k1 = k2. б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
5. Условия перпендикулярности двух прямых: а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е. а) параллельны тогда и только тогда, когда векторы а и b коллинеарны; б) перпендикулярны тогда и только тогда, когда векторы а и b перпендикулярны, т. е. когда а • b = 0. Отсюда получаем необходимые и достаточные условия параллельности и перпендикулярности двух прямых, заданных каноническими уравнениями. Для того чтобы прямые
были параллельны, необходимо и достаточно чтобы выполнялось условие a1b1 + a2b2 + a3b3 = 0. Билет 18 Плоскость в пространстве Составим уравнение плоскости, проходящей через данную точку
Билет 19
Составим теперь уравнение плоскости, проходящей через данную точку Для того чтобы провести плоскость через три данные точки
Билет 20 Частные случая общего уравнения плоскости Общее уравнение плоскости называется полным, если Уравнение в отрезках. Полное уравнение плоскости в пространстве может быть записано в следующем виде:
Полагая а = - D/А, b = - D/B, c = - D/C, получим эквивалентное уравнение
называемое уравнением плоскости в отрезках. Числа а, b, с в этом уравнении имеют простой геометрический смысл (рис. 2): они равны величинами отрезков, которые отсекает плоскость на осях координат.
Билет 21 Рассмотрим неполные уравнения плоскости: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Билет 22 Нормальное уравнение плоскости Уравнение вида Чтобы вычислить расстояние l от точки Нормальное уравнение можно получить из общего уравнения (1), умножив его на нормирующий множитель Косинусы углов между прямой и осями координат называют направляющими косинусами, a – угол между прямой и осью
тем самым, нормальное уравнение можно записать в виде
Расстояние от точки
Билет 23 Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей. Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей. Если заданы уравнения плоскостей A1x+ B1y+ C1z+ D1 = 0 и A2x+ B2y+ C2z+ D2 = 0, то угол между плоскостями можно найти, используя следующую формулу

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 1. Модуль смешанного произведения некомпланарных векторов
1. Модуль смешанного произведения некомпланарных векторов  равен объему
равен объему 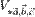 параллелепипеда, построенного на этих векторах. Произведение
параллелепипеда, построенного на этих векторах. Произведение  положительно, если тройка векторов
положительно, если тройка векторов 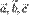 — правая, и отрицательно, если тройка
— правая, и отрицательно, если тройка  — левая, и наоборот.
— левая, и наоборот. равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы 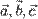 компланарны:
компланарны: векторы
векторы  — угол между векторами
— угол между векторами  и
и  . Модуль векторного произведения (по геометрическому свойству 1) равен площади
. Модуль векторного произведения (по геометрическому свойству 1) равен площади 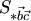 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  и
и 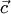 : . Поэтому
: . Поэтому  . Алгебраическое значение
. Алгебраическое значение  длины проекции вектора
длины проекции вектора  , равно по модулю высоте
, равно по модулю высоте  параллелепипеда, построенного на векторах
параллелепипеда, построенного на векторах  (рис. 1.47). Поэтому модуль смешанного произведения равен объему
(рис. 1.47). Поэтому модуль смешанного произведения равен объему  этого параллелепипеда:
этого параллелепипеда:
 . Если тройка
. Если тройка  и смешанное произведение
и смешанное произведение  положительно. Если же тройка
положительно. Если же тройка  и смешанное произведение
и смешанное произведение  отрицательно.
отрицательно. или
или 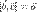 (т.е.
(т.е.  ),или
),или  (т.е. вектор
(т.е. вектор 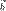 и
и  ). В каждом случае векторы
). В каждом случае векторы  компланарны
компланарны ,
,  и
и  были компланарны, необходимо и достаточно, чтобы
были компланарны, необходимо и достаточно, чтобы  .
. векторов
векторов  — векторное произведение вектора
— векторное произведение вектора  на векторное произведение векторов
на векторное произведение векторов 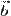 и
и 
 ,
,  и
и  называют вектор
называют вектор  .
. .
.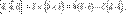
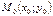 и перпендикулярно данному вектору
и перпендикулярно данному вектору 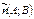 .
. прямой l:
прямой l:  . Это значит, что
. Это значит, что 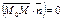 - векторное уравнение прямой, проходящей через точку
- векторное уравнение прямой, проходящей через точку  .
.  . Обозначив
. Обозначив  , получим:
, получим:  - общее уравнение прямой, если
- общее уравнение прямой, если  или
или  .
. и
и  , можно получить уравнение
, можно получить уравнение  . При этом
. При этом  , где a - угол наклона прямой к положительному направлению оси Ox, а b = величина отрезка, отсекаемого прямой на оси Oy.
, где a - угол наклона прямой к положительному направлению оси Ox, а b = величина отрезка, отсекаемого прямой на оси Oy. Составим теперь уравнение прямой, проходящей через данную точку
Составим теперь уравнение прямой, проходящей через данную точку 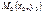 параллельно
параллельно  .
. прямой l:
прямой l: 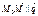 . Это значит, что
. Это значит, что 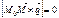 - векторное уравнение прямой. Раз
- векторное уравнение прямой. Раз  , то
, то  - каноническое уравнение прямой.
- каноническое уравнение прямой. и
и  . В качестве точки
. В качестве точки  возьмём одну из них, а в качестве
возьмём одну из них, а в качестве  возьмём
возьмём 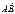 . Тогда
. Тогда  - уравнение прямой, проходящей через две данные точки.
- уравнение прямой, проходящей через две данные точки.
 , то получим
, то получим  - параметрические уравнения прямой.
- параметрические уравнения прямой. ,
,  . Тогда
. Тогда  .
. ,
,  . Тогда
. Тогда 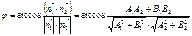 .
. ,
, 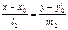 . Тогда
. Тогда 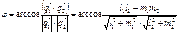 .
. называют полным, если
называют полным, если 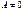 ,
, 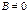 и
и  .
. ,
,  . Тогда
. Тогда  . Здесь a и b – величины отрезков, отсекаемых прямой на осях Ox и Oy соответственно.
. Здесь a и b – величины отрезков, отсекаемых прямой на осях Ox и Oy соответственно. – параллельна оси x.
– параллельна оси x.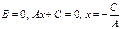 – параллельна оси y.
– параллельна оси y. – проходит через начало координат.
– проходит через начало координат. – ось x.
– ось x. – ось y.
– ось y. ,
,  , где a - угол между нормалью к прямой и осью Ox, причём нормаль направлена из начала координат в сторону прямой и p – расстояние от начала координат до прямой.
, где a - угол между нормалью к прямой и осью Ox, причём нормаль направлена из начала координат в сторону прямой и p – расстояние от начала координат до прямой.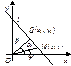
 справедливо для
справедливо для  . Преобразуем это выражение:
. Преобразуем это выражение: 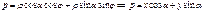 (Т.к.
(Т.к. 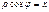 и
и  ), или
), или 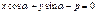 .
.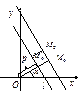 Нормальное уравнение прямой применяется для вычисления расстояния от данной точки плоскости до прямой. Рассмотрим случай, когда точка
Нормальное уравнение прямой применяется для вычисления расстояния от данной точки плоскости до прямой. Рассмотрим случай, когда точка  и точка O лежат по одну сторону от прямой. Расстояние от
и точка O лежат по одну сторону от прямой. Расстояние от  то l равно
то l равно  . Рассмотрим нормальное уравнение прямой, параллельной l (
. Рассмотрим нормальное уравнение прямой, параллельной l (  ):
):  , где
, где  . Т.к. точка
. Т.к. точка  , то
, то  – верное равенство, значит,
– верное равенство, значит,  .
.  . Если точка
. Если точка  и точка O лежат по одну сторону от прямой l, то расстояние от
и точка O лежат по одну сторону от прямой l, то расстояние от  . Следовательно, расстояние от
. Следовательно, расстояние от  .
. к
к  ). Очевидно, что коэффициенты пропорциональны, т.е.
). Очевидно, что коэффициенты пропорциональны, т.е. 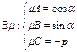 . Тогда
. Тогда 
 и знак m - нормирующий множитель, противоположен знаку C.
и знак m - нормирующий множитель, противоположен знаку C. умножить на так называемый нормирующий множитель, который равен
умножить на так называемый нормирующий множитель, который равен  . Знак нормирующего множителя берется противоположным знаку слагаемого С. Если C = 0, то знак нормирующего множителя не имеет значения и может быть выбран произвольно.
. Знак нормирующего множителя берется противоположным знаку слагаемого С. Если C = 0, то знак нормирующего множителя не имеет значения и может быть выбран произвольно. .
. - первая прямая,
- первая прямая,  - вторая прямая. Для того чтобы получить одну из биссектрис, необходимо приравнять левые части уравнений:
- вторая прямая. Для того чтобы получить одну из биссектрис, необходимо приравнять левые части уравнений: 
 . Для второй:
. Для второй:  .
. и
и  заданы общими уравнениями
заданы общими уравнениями и
и 
 и
и  (напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами
(напомним, что угол между прямыми измеряется от 0° до 90°), а через ψ – угол между нормальными векторами  и
и  этих прямых. Если ψ ≤ 90°, то φ = ψ. Если же ψ > 90°, то φ = 180° – ψ. В обоих случаях верно равенство
этих прямых. Если ψ ≤ 90°, то φ = ψ. Если же ψ > 90°, то φ = 180° – ψ. В обоих случаях верно равенство  Из теоремы 11.10 следует, что
Из теоремы 11.10 следует, что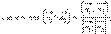


 заданы уравнениями с угловыми коэффициентами
заданы уравнениями с угловыми коэффициентами  и
и 
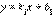 и
и 

 и выражение для косинуса угла между этими прямыми будет иметь вид:
и выражение для косинуса угла между этими прямыми будет иметь вид:
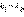 то cos φ = 1 и φ = 0, то есть прямые параллельны или совпадают. С другой стороны, если прямые параллельны, то φ = 0 или cos φ = 1. Подставляя в правую часть вместо cos φ его значение 1, умножая обе части на знаменатель и возводя в квадрат, получим
то cos φ = 1 и φ = 0, то есть прямые параллельны или совпадают. С другой стороны, если прямые параллельны, то φ = 0 или cos φ = 1. Подставляя в правую часть вместо cos φ его значение 1, умножая обе части на знаменатель и возводя в квадрат, получим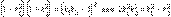

 то cos φ = 0 и
то cos φ = 0 и  то есть прямые перпендикулярны. Обратно, если прямые перпендикулярны, то
то есть прямые перпендикулярны. Обратно, если прямые перпендикулярны, то  или cos φ = 0. Отсюда следует с необходимостью
или cos φ = 0. Отсюда следует с необходимостью 
 и
и  формулируются следующим образом.
формулируются следующим образом.





 Прямые с направляющими векторами а и b:
Прямые с направляющими векторами а и b:
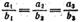 В случае, если какое-либо из чисел b1, b2, b3 равно нулю, то должно обращаться в нуль соответствующее ему число a1, a2, a3. Для перпендикулярности прямых необходимо и достаточно, чтобы выполнялось условие
В случае, если какое-либо из чисел b1, b2, b3 равно нулю, то должно обращаться в нуль соответствующее ему число a1, a2, a3. Для перпендикулярности прямых необходимо и достаточно, чтобы выполнялось условие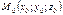 перпендикулярно данному вектору
перпендикулярно данному вектору 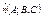 . Пусть
. Пусть  - произвольная точка плоскости. То, что M принадлежит плоскости, означает, что
- произвольная точка плоскости. То, что M принадлежит плоскости, означает, что 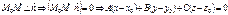 . Раскрыв скобки и обозначив
. Раскрыв скобки и обозначив  , получим
, получим  - общее уравнение плоскости, если
- общее уравнение плоскости, если 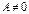 ,
, 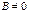 или
или  . Ненулевой вектор, перпендикулярный данной плоскости называется нормальным вектором этой плоскости.
. Ненулевой вектор, перпендикулярный данной плоскости называется нормальным вектором этой плоскости. параллельно двум данным векторам
параллельно двум данным векторам  и
и  . Возьмём
. Возьмём  , принадлежащую нашей плоскости. Это значит, что
, принадлежащую нашей плоскости. Это значит, что  ,
,  и
и  - уравнение плоскости, проходящей через данную точки параллельно двум данным векторам.
- уравнение плоскости, проходящей через данную точки параллельно двум данным векторам. ,
,  ,
,  достаточно взять
достаточно взять  и
и  . Тогда
. Тогда 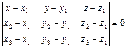 и есть искомое уравнение плоскости.
и есть искомое уравнение плоскости. ,
, 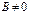 ,
,  . Тогда можно получить уравнение плоскости в отрезках:
. Тогда можно получить уравнение плоскости в отрезках: 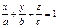 , где
, где  ,
,  и
и  . Здесь a, b и c – величины отрезков, отсекаемых плоскостью на осях Ox, Oy и Oz соответственно.
. Здесь a, b и c – величины отрезков, отсекаемых плоскостью на осях Ox, Oy и Oz соответственно.
 ,
, - плоскость параллельна оси Ox.
- плоскость параллельна оси Ox. - плоскость параллельна оси Oy.
- плоскость параллельна оси Oy. - плоскость параллельна оси Oz.
- плоскость параллельна оси Oz.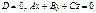 - плоскость проходит через начало координат.
- плоскость проходит через начало координат.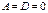 - ось Ox принадлежит плоскости.
- ось Ox принадлежит плоскости. - ось Oy принадлежит плоскости.
- ось Oy принадлежит плоскости. - ось Oz принадлежит плоскости.
- ось Oz принадлежит плоскости. - плоскость xOy.
- плоскость xOy. - плоскость yOz.
- плоскость yOz. - плоскость xOz.
- плоскость xOz. называют нормальным уравнением плоскости, если
называют нормальным уравнением плоскости, если 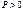 , а
, а  ,
,  и
и 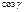 - направляющие косинусы нормального вектора, направленного из начала координат в сторону плоскости.
- направляющие косинусы нормального вектора, направленного из начала координат в сторону плоскости. до плоскости, нужно привести уравнение плоскости к нормальному виду и тогда
до плоскости, нужно привести уравнение плоскости к нормальному виду и тогда  .
.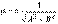 , знак m противоположен знаку
, знак m противоположен знаку 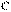 , чтобы
, чтобы  .
.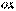 , b – между прямой и осью
, b – между прямой и осью  :
: ,
, .
.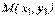 до прямой определяется по формуле
до прямой определяется по формуле