
|
|
Ранг и базис системы векторовОпределение 1. Рангом системы векторов называется максимальное число линейно независимых векторов (Система векторов Определение 2. Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов. Теорема. Любой вектор системы можно представить в виде линейной комбинации (Линейной комбинацией системы векторов называется выражение вида Доказательство.Пусть система 1 случай. Вектор 2 случай. Вектор Рассмотрим систему векторов Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису. Вычитая эти равенства, получим Учитывая линейную независимость векторов базиса, получим Следовательно, разложение вектора по базису единственно. Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.
Вычисление ранга системы векторов можно свести к вычислению ранга матрицы. Т.к. ранг системы векторов равен рангу матрицы, столбцами (строками) которой являются векторы этой системы. Пример. Найти ранг системы векторов Составим матрицу из координат векторов и найдем ее ранг.
Ранг данной системы векторов равен трем, т.е. она имеет три линейно независимых вектора.
Системы линейных уравнений Определение:Системой
Систему (1) можно записать также в виде
или в виде
Но наиболее удобной формой записи системы (15.1) является матричная запись. Введем следующие матрицы: матрица системы
с помощью введенных обозначений систему (1) можно записать в виде
Однородная, неоднородная СЛАУ. Совместная, несовместная СЛАУ. Система называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений. Определённая, неопределённая СЛАУ. Если СЛАУ имеет решение и при том единственное, то её называют определённой а если решение неединственное – то неопределённой. МАТРИЧНЫЕ УРАВНЕНИЯ Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Найдем произведение т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением. Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Формулы Крамера Метод Крамера состоит в том, что мы последовательно находим главный определитель системы, т.е. определитель матрицы А : D = det (ai j) и n вспомогательных определителей D i (i= Формулы Крамера имеют вид: D × x i = D i (i = Из этого следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы: если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам: x i = D i / D. Если главный определитель системы D и все вспомогательные определители D i = 0 (i= Теорема (правило Крамера): Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём Доказательство: Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения: Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и Наконец несложно заметить, что Таким образом, получаем равенство: Аналогично выводятся равенства Теорема Кронекера - Капелли. Система линейных уравнений является совместной тогда и только тогда, когда ранг матрицы системы Доказательство: Оно распадается на два этапа. 1. Пусть система имеет решение. Покажем, что Пусть набор чисел 2. Пусть
Положим
В силу равенства (1) В рассмотренной выше системе Замечание:Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой - в противном случае) системы.
называется линейно зависимой, если один из векторов системы можно представить в виде линейной комбинации остальных векторов системы, и линейно независимой - в противном случае) системы. .
. , где с1, с2, …, сk - некоторые числа) векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.
, где с1, с2, …, сk - некоторые числа) векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно. имеет базис
имеет базис  .
. - из базиса. Следовательно, он равен одному из векторов базиса, допустим
- из базиса. Следовательно, он равен одному из векторов базиса, допустим  . Тогда
. Тогда  =
=  .
. - не из базиса. Тогда r>k.
- не из базиса. Тогда r>k. . Данная система является линейно зависимой, так как
. Данная система является линейно зависимой, так как  - базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с1, с2, …, сk, с, не все равные нулю, такие, что
- базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с1, с2, …, сk, с, не все равные нулю, такие, что  =
=  . Очевидно, что
. Очевидно, что  (если с=0, то базис системы является линейно зависимым).
(если с=0, то базис системы является линейно зависимым).  .
. ,
,  .
. .
. .
.

 ~
~  ~
~  ~
~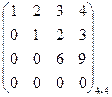 ~
~  , r(А)=3,
, r(А)=3,  =1¹0.
=1¹0. линейных уравнений с
линейных уравнений с 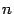 неизвестными называется система уравнений вида
неизвестными называется система уравнений вида
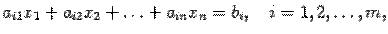
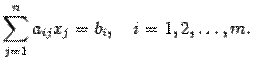
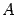 , столбец неизвестных
, столбец неизвестных  и столбец свободных членов
и столбец свободных членов  ,
,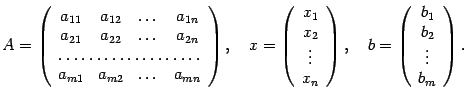
 и неоднородной в противном случае.
и неоднородной в противном случае. Рассмотрим матрицу системы
Рассмотрим матрицу системы  и матрицы столбцы неизвестных и свободных членов
и матрицы столбцы неизвестных и свободных членов 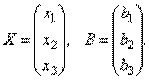
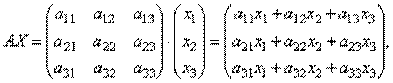
 или короче A∙X=B.
или короче A∙X=B. . Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B.
. Поскольку A-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A-1B. ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.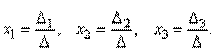


 .
.
 .
.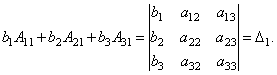
 . Следовательно,
. Следовательно,  .
. и
и  , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы. .
. .
. является решением системы. Обозначим через
является решением системы. Обозначим через 
 -ый столбец матрицы
-ый столбец матрицы  . Тогда
. Тогда 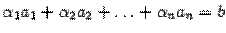 , то есть столбец свободных членов является линейной комбинацией столбцов матрицы
, то есть столбец свободных членов является линейной комбинацией столбцов матрицы  . Предположим, что
. Предположим, что  . Тогда по
. Тогда по  . Выберем в
. Выберем в  . Он имеет порядок
. Он имеет порядок  . Столбец
. Столбец  , где
, где  -- определитель, который получается из минора
-- определитель, который получается из минора  . Если столбец
. Если столбец  проходил через минор M, то в
проходил через минор M, то в  , будет два одинаковых столбца и, следовательно,
, будет два одинаковых столбца и, следовательно,  . Если столбец
. Если столбец  не проходил через минор
не проходил через минор 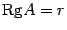 , то
, то  . Таким образом,
. Таким образом,  , что противоречит определению базисного минора. Значит, предположение, что
, что противоречит определению базисного минора. Значит, предположение, что  , неверно.
, неверно. . Тогда по теореме о базисном миноре в матрице
. Тогда по теореме о базисном миноре в матрице 
 ,
,  ,
,  ,
,  , остальные неизвестные возьмем равными нулю. Тогда при этих значениях
, остальные неизвестные возьмем равными нулю. Тогда при этих значениях  получим
получим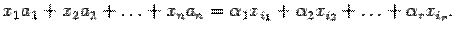
 . Последнее равенство означает, что набор чисел
. Последнее равенство означает, что набор чисел  является решением системы. Существование решения доказано.
является решением системы. Существование решения доказано. , и система является совместной. В системе
, и система является совместной. В системе  ,
,  , и система является несовместной.
, и система является несовместной. и
и  , ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.
, ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.