
|
|
Прямая линия на плоскости
Тест 1 1. Какие сведения о прямой линии надо знать, чтобы написать какое-нибудь ее уравнение? 2 .Верно ли утверждение: «Всякое уравнение вида 3. Верно ли, что вектор 4. Прямая задана уравнением: 5. Прямая задана параметрическими уравнениями: 6. Продолжите определение: « Вектор 7. Продолжите определение: « Вектор 8. Напишите уравнение прямой по точке 9. Укажите точки, лежащие на осях координат, через которые проходит прямая 10. Установите соответствие между уравнениями прямой линии на плоскости 1) 5) 8) а) общее уравнение, б) каноническое уравнение, в) параметрические уравнения, г) уравнение по точке и угловому коэффициенту, д) по точке и нормальному вектору, е) уравнение прямой в отрезках.
Тест 2 1. Укажите, какие из следующих уравнений определяют прямую линию: 1) 4) 2. Укажите нормальный вектор прямой 3. Укажите направляющий вектор прямой 4. Установите соответствие между уравнениями прямых и парами чисел, определяющими их направляющие векторы: 1) а) 5. Среди указанных уравнений укажите уравнения, определяющие одну и ту же прямую: 1) 6. Параметрические уравнения прямой 1) 7. Уравнение прямой, проходящей через точку 8. Прямые 1) параллельны 2) перпендикулярны 3) совпадают 4) пересекаются
9. Прямая 1) имеет угловой коэффициент 2) имеет нормальный вектор 3) проходит через начало координат; 4) отсекает на осях OX и OY отрезки соответственно 5 и 2,5. 10. Острый угол между прямыми 1) 11. Расстояние от точки 12. Написать уравнение серединного перпендикуляра к отрезку
Тест 3 1. Уравнение прямой, содержащей точку 1) 2. Ордината точки пересечения прямых 3. Написать уравнение прямой, проходящей через точку 4. Для прямой, проходящей через точку А(1,0) параллельно прямой 5.Треугольник задан координатами своих вершин: 6. Написать уравнение прямой, проходящей через точку пересечения прямых 7. Написать уравнение полуплоскости с границей 8. Проекцией точки a. (-3; -12 ); b. (3; -2 ); c. (0; -7 ); d. (6; 2 ). 9. Треугольник задан координатами своих вершин:
Прямая в пространстве Тест 1
1. Если 2. Прямая l: a. (1; 2; 3); b. (1; -2; 1); c. (1; 1; -1); d. (1; -2; -1).
3. Прямые a. 3; b. 4; c. 6; d. 10. 4.Прямые
a. -1; b. 3; c. 1; d. 2. 5. Прямые a. Скрещиваются; b. Пересекаются; c. Параллельны; d. Совпадают. e. 4 6. Косинус угла между прямыми 7. Если 8.Прямая
9. Если
10. Прямая 1) параллельна вектору 3) перпендикулярна вектору
11. Проекцией точки
Дидактические материалы для организации самостоятельной работы студентов физического факультета по дисциплине « Линейная алгебра и аналитическая геометрия Ярославль, 2009
ЛИТЕРАТУРА, РЕКОМЕНДУЕМАЯ ДЛЯ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ 1.1. Основная литература 1. Ильин В.А., Позняк Э.Г., Аналитическая геометрия, М., 1981 2. Ильин В.А., Позняк Э.Г., Линейная алгебра., М.,1984. 3. Головина Л.И. Линейная алгебра и некоторые ее приложения, М., 1979. 4. Клетеник Д.В. Сборник задач по аналитической геометрии. М., 1979. 5. Проскуряков И.В. Сборник задач по алгебре., М., 1970. 6. Большаков Ю.И., Медведева Л.Б., Математика для студентов в задачах и упражнениях по физике: учеб. пособие; Яросл. гос. ун-т им. П.Г. Демидова. – Ярославль: ЯрГУ, 2009.–132 с. 7. Методические указания «Дидактические материалы для организации самостоятельной работы студентов-физиков по курсу «Линейная алгебра и аналитическая геометрия». . – Ярославль: ЯрГУ, 1997.–24 с.
1.2. Дополнительная литература 1. Мальцев А.И. Основы линейной алгебры, М., 1970 2. Гельфанд И.М. Лекции по линейной алгебре, М., 1971. 3. Федорчук В.В. Курс аналитической геометрии и линейной алгебры. Изд-во Московского ун-та., 1990. 4. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре, М., 1973. 5. Александров П.С. Курс аналитической геометрии и линейной алгебры., М., 1979.
2.СОДЕРЖАНИЕ КУРСА ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ Тема 1. Понятие линейного векторного пространства. Примеры. Пространство однотипных матриц. Литература:[1], гл. 2 § 1; [2], гл. 1 § 1, гл. 11 § 1. Домашнее задание: Операции над матрицами (написать конспект), [5], №790, 796, 827.
Тема 2. Решение систем линейных уравнений. Однородная система, пространство ее решений. Литература:[2], гл. 3 § 1; [3], ч. 1 § 9, § 11. Домашнее задание: [5], №692, 693, 699.
Тема 3. Линейная зависимость векторов. Ранг и базис системы векторов. Ранг матрицы. Литература:[2], гл. 2 § 1, § 2; [1], гл. 2 § 4;[10], гл. 2 § 7-10; [2], гл. 3 § 1-4; [3], гл. 1 § 7,9,10. Домашнее задание: [5], №674, 681, 702, 697, 704.
Тема 4. Определители. Правило Крамера. Литература:[2], гл. 1 § 2,3; [3], гл. 1 § 2-5;[10], гл. 3 § 11. Домашнее задание: [5], №11, 56, 262, 420, 435, 556.
Тема 5. Линейные операции над векторами. Скалярное, векторное, смешанное произведение векторов. Литература:[1], гл. 2 § 2,3. Домашнее задание: [4], №709 (3,4), 796 (1), 742, 874 (3), 849, 827.
Тема 6. Прямоугольная декартова система координат. Полярная система координат. Решение простейших задач геометрии в координатах. Литература:[1], гл. 1 § 2-4. Домашнее задание: [4], №637, 858, 877, 13 (4).
Тема 7. Прямая и плоскость в пространстве. Прямая линия на плоскости. Литература:[1], гл. 5 § 1-5. Домашнее задание: [4], №234, 239, 247, 293; 915, 921, 934, 1021, 1043, 1062, 1065, 1072, 1076, 1077.
Тема 8. Кривые и поверхности второго порядка. Литература:[1], гл. 6 § 1-3, гл. 7 2,3. Домашнее задание: [4], №444 (5,10), 532 (1,5), 600, 593.
Тема 9. Подпространства линейного пространства, их сумма и пересечение. Преобразование координат векторов при переходе к новому базису. Литература:[2], гл. 2 § 2-4; [3], гл. 2 § 6, § 10-11. Домашнее задание: [5], №1315, 1317, 1321, 1278.
Тема 10. Линейные операторы. Приведение матрицы линейного оператора к каноническому виду. Литература:[2], гл. 5 § 1-3; [3], гл. 3 § 4,5,7,10. Домашнее задание: [5], №1436, 1443, 1453, 1469, 1481, 1487, 1534.
Тема 11. Евклидово пространство над полем вещественных и полем комплексных чисел. Литература:[2], гл. 4 § 1-3. Домашнее задание: [5], №1363, 1367, 1371.
Тема 12. Самосопряженные операторы в вещественном и комплексном евклидовых пространствах. Литература:[2], гл. 5 § 4,5,7. Домашнее задание: [5], №1542, 1546, 1556.
Тема 13. Унитарные операторы. Ортогональные операторы вещественного евклидова пространства. Литература:[2], гл. 5 § 7-9. Домашнее задание: [5], №1561, 1570, 1572.
Тема 14. Билинейные и квадратичные формы. Литература:[2], гл. 7 § 1-4; [1], гл. 6 § 5; [3], гл. 6 § 1-4, гл. 7 § 1-3. Домашнее задание: [5], №1178, 1184, 1188, 1213, 1250.
3. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ НА ПЕРВЫЙ СЕМЕСТР
3.1.Темы для самостоятельного изучения 1. Операции над матрицами, их свойства. Отыскание обратной матрицы. Литература: [2], гл.1 §1 2. Специальные способы вычисления определителей Литература: [2], гл.1 §2; [3], гл.1 §3; [5], §5. 3.Физические приложения скалярного и векторного произведения. Литература: [1], гл.2 §2,3.
Указание. По каждой из предложенных тем необходимо составить краткий конспект, в котором обязательно привести примеры, иллюстрирующие положения теории.
Вопросы к коллоквиуму
1. Понятие линейного векторного пространства. Примеры линейных векторных пространств. 2. Понятие системы линейных уравнений и ее решения. Совместные и несовместные системы, определенные и неопределенные. Элементарные преобразования системы. Равносильные системы. 3. Правило Жордана-Гаусса исключения переменной из всех уравнений системы, кроме одного, и его применение к решению систем. 4. Однородная система уравнений и свойства ее решений. Связь решений однородной и неоднородной систем. 5. Линейно зависимые и линейно независимые системы векторов. Необходимое и достаточное условие линейной зависимости. Примеры. 6. Свойства линейно зависимых и линейно независимых систем. Линейная зависимость векторов пространства 7. Понятие базиса системы векторов. Теорема о двух различных базисах одной и той же системы векторов. 8. Ранг системы векторов, его свойства. Размерность векторного пространства. 9. Ранг матрицы. 10. Операции над матрицами, их свойства. 11. Обратная матрица. Матричная запись системы линейных уравнений и ее решение с помощью обратной матрицы. 12. Понятие определителя квадратной матрицы. 13. Понятие минора и алгебраического дополнения. Правило Лапласа разложения определителя по элементам какой-либо строки или столбца. 14. Свойства определителей, методы вычисления определителей. 15. Правило Крамера решения систем линейных уравнений. Замечание: коллоквиум проводится в виде собеседования преподавателя с каждым студентом. Выясненные в процессе собеседования затруднения в усвоении материала обсуждаются на групповой консультации. К коллоквиуму студенты обязаны выполнить следующее домашнее задание. 3.3.Индивидуальная домашняя контрольная работа №1
Выполняется по задачникам: 1) Проскуряков И.В. Сборник задач по линейной алгебре. М. 1970 (первые 10 задач). 2) Большаков Ю.И., Медведева Л.Б., Математика для студентов в задачах и упражнениях по физике: учеб. пособие; Ярославль: ЯрГУ, 2009 (последняя задача). В.1 699 679 661 790 819 844 861 56 225 232 2а) В.2 702 674 620 793 824 843 962 55 221 229 2в) В.З 701 681 621 792 825 842 867 54 214 228 2г) В.4 700 680 622 791 827 841 868 53 213 227 5 В.5 703 675 619 795 828 840 869 52 212 226 6 В.6 704 643 612 797 827 845 863 44 224 268 7 В.7 706 644 613 798 825 846 964 45 225 269 8 В.8 707 646 623 806 812 847 865 46 226 270 9 В.9 706 649 627 810 813 934 870 47 227 271 10 В.10 703 650 608 812 791 935 861 48 212 275 11 В.11 709 652 609 824 794 836 862 49 227 446 12 В.12 710 653 610 825 829 839 866 50 228 447 13 В.13 711 660 611 828 831 840 867 51 229 448 14 В.14 715 661 617 834 832 841 868 57 232 450 15 B.I5 716 665 624 791 814 842 869 58 233 428 16 В.16 717 666 625 820 821 843 863 59 247 429 1в) В.17 727 676 626 795 822 844 864 60 246 434 1г) В.18 728 667 635 790 823 857 865 61 249 440 5 В.19 730 668 615 796 825 848 870 62 250 438 6 В.20 731 669 626 792 829 849 876 63 251 439 7 В.21 691 654 611 827 795 861 872 50 229 445 8 В.22 695 650 613 828 798 862 845 54 227 447 9 В.23 697 649 621 829 804 863 888 55 232 448 10 В.24 698 660 622 632 808 864 841 58 237 450 11 В.25 703 651 627 634 809 865 884 59 239 457 12

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 есть уравнение прямой линии на плоскости
есть уравнение прямой линии на плоскости  »?
»?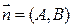 будет нормальным вектором прямой
будет нормальным вектором прямой 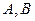 не равны 0 одновременно).
не равны 0 одновременно). Что можно сказать про точку с координатами (
Что можно сказать про точку с координатами (  ) и каков смысл параметров
) и каков смысл параметров  ?
? Укажите координаты направляющего вектора и укажите точку, через которую она проходит.
Укажите координаты направляющего вектора и укажите точку, через которую она проходит.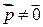 называется направляющим вектором прямой
называется направляющим вектором прямой 
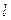 , если найдутся такие две точки
, если найдутся такие две точки  и
и  , что …
, что … называется нормальным вектором прямой
называется нормальным вектором прямой  и нормальному вектору
и нормальному вектору  .
.
 2)
2)  3)
3)  4)
4) 
 6)
6)  7)
7) 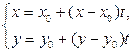 и их названиями:
и их названиями: ; 2)
; 2)  ; 3)
; 3)  (в полярных координатах);
(в полярных координатах); ; 5)
; 5) 
 .
. .
. ; 2)
; 2)  4 3)
4 3)  ; 4)
; 4)  5)
5) 
 ; б)
; б)  ; в)
; в)  ; г)
; г) 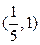 ; д)
; д)  .
. ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 
 могут иметь вид
могут иметь вид 2)
2)  3)
3)  4)
4) 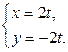
 под углом
под углом  к оси
к оси 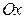 , имеет вид : 1)
, имеет вид : 1)  , 2)
, 2)  , 3)
, 3)  .
.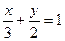 и
и 

 ;
; ;
; и
и  в градусах равен:
в градусах равен: , 2)
, 2)  , 3)
, 3)  , 4)
, 4) 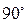 .
. до прямой
до прямой  равно …
равно … , где
, где  ,
,  .
. 2)
2)  ; 3)
; 3)  ; 4)
; 4) 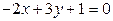 .
. и
и  равна
равна и перпендикулярной к прямой
и перпендикулярной к прямой 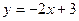 .
. , абсцисса точки пересечения с осью ОХ равна
, абсцисса точки пересечения с осью ОХ равна . Написать уравнение прямой, на которой лежит медиана, проходящая через вершину
. Написать уравнение прямой, на которой лежит медиана, проходящая через вершину  .
. и
и  :
:  и написать уравнение прямой, проходящей через эту точку перпендикулярно
и написать уравнение прямой, проходящей через эту точку перпендикулярно  , в которой лежит точка
, в которой лежит точка 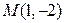 .
. на прямую x=3t; y=5 t-7 является точка с координатами:
на прямую x=3t; y=5 t-7 является точка с координатами: . Написать уравнение прямой, на которой лежит биссектриса угла
. Написать уравнение прямой, на которой лежит биссектриса угла  - параметрические уравнения прямой, проходящей через точку
- параметрические уравнения прямой, проходящей через точку 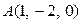 параллельно вектору
параллельно вектору  , то
, то 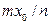 равно
равно заданная пересечением двух плоскостей, имеет направляющий вектор с координатами:
заданная пересечением двух плоскостей, имеет направляющий вектор с координатами: и
и  параллельны при
параллельны при  равном:
равном: и
и 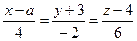 совпадают при a, равном:
совпадают при a, равном: и
и 
 и
и  равен
равен параллельно прямой
параллельно прямой  , то
, то 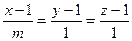 проходит перпендикулярно векторам
проходит перпендикулярно векторам  и
и  Число m равно
Число m равно и
и  , то
, то  равно
равно
 ; 2) параллельна вектору
; 2) параллельна вектору  ;
; на прямую
на прямую  является точка с координатами
является точка с координатами 
 ого порядка (по желанию).
ого порядка (по желанию). .
.