
|
|
МАТЕРИАЛЫ ТЕКУЩЕГО И ИТОГОВОГО КОНТРОЛЯЛинейная алгебра и аналитическая геометрия
Направление подготовки 210400 Телекоммуникации 210302 Радиотехника
Профиль подготовки _____________________
Квалификация (степень) выпускника Бакалавр
Форма обучения Очная
Ярославль 2010
Аннотация академического курса «Линейная алгебра и аналитическая геометрия» Базовой части профессионального цикла Для специальности 010700 Физика
Форма обучения очная Факультет физический Кафедра общей математики Курс___1_____ семестр ________1-2______
Общая трудоемкость дисциплины 5 з.е. 180 час. Лекции _____90_______ (час.) Практические занятия __90(час.) Форма контроля экзамены в 1 и 2 семестрах.
Краткое содержание Дисциплина «Аналитическая геометрия и линейная алгебра», которая вошла в учебный план подготовки бакалавровпо направлениям подготовки 210400 – «Телекоммуникации», 210302 – «Радиотехника», знакомит студентов с основными понятиями, задачами и методами аналитической геометрии и линейной алгебры, взаимосвязями этих разделов математики с другими математическими и физическими дисциплинами, а также их практическими приложениями.
Содержание курса составляют следующие вопросы: - векторная алгебра и координатный метод на плоскости и в пространстве; - прямая линия на плоскости и в пространстве; - плоскость, прямая и плоскость в пространстве; - кривые и поверхности второго порядка; - матрицы и определители; - системы линейных уравнений; - линейные пространства; евклидовы и унитарные пространства; - Линейные операторы в конечномерных пространствах, в том числе евклидовом и унитарном; - Билинейные и квадратичные формы.
1. Цели освоения дисциплины Целью дисциплины является ознакомление слушателей с основными понятиями, задачами и методами аналитической геометрии и линейной алгебры, а также их ролью и использованием в других математических и специальных дисциплинах, практическими приложениями. Изучение дисциплины «Аналитическая геометрия и линейная алгебра» обеспечивает приобретение знаний и умений в соответствии с государственным образовательным стандартом, содействует формированию научного мировоззрения и математической культуры, способствует развитию абстрактного мышления и пространственного воображения
2. Место дисциплины в структуре ООП бакалавриата Учебный курс «Аналитическая геометрия и линейная алгебра» для студентов физического факультета относится к циклу естественнонаучных дисциплин и является там базовым. Знания и навыки, полученные при изучении этого курса, находят широкое применение при изучении других дисциплин, например таких как «Математический анализ», «Дифференциальные уравнения», «Векторный и тензорный анализ», «Механика», «Методы математической физики».
3. Требования к результатам освоения содержания дисциплины Процесс изучения дисциплины направлен на формирование элементов следующих компетенций в соответствии с ФГОС ВПО по данному направлению: а) общекультурных (ОК): ОК-5, ОК-6, ОК-8, ОК-11, б) профессиональных (ПК): ПК-1, ПК-2, ПК-3, ПК-4, ПК-5, ПК-6, ПК-7, ПК-8, ПК-9, ПК-10, ПК-11, ПК-12, ПК-15, ПК-16, ПК-19, ПК-20, ПК-21, ПК-22, ПК-23, ПК-24, ПК-25, ПК-27, ПК-29. В результате изучения дисциплины слушатели должны: Иметь представление -о функциональных линейных пространствах; -об евклидовых и неевклидовых пространствах, в частности о псевдоевклидовой плоскости и ее геометрии, о плоскости Лобачевского; -об изоморфизме линейных пространств и других алгебраических структур; -о канонической форме матриц самосопряженного и унитарного операторов; -о группах преобразований Галилея и Лоренца; Знать -понятие линейного пространства и примеры линейных пространств; -определение линейно зависимых и линейно независимых векторов, базиса системы векторов и векторного пространства, координат вектора в данном базисе; -понятие подпространства, суммы и пересечения подпространств; -понятие системы линейных уравнений и ее решения, методы решения систем (метод Гаусса, правило Крамера, матричный метод); -операции над матрицами; -определение определителя квадратной матрицы, свойства определителей и методы их вычисления, приложения определителей; -понятия скалярного, векторного, смешанного произведений векторов, их приложения в геометрии и физике; -виды систем координат на плоскости и в пространстве; -все виды уравнений прямой линии на плоскости и в пространстве; -уравнения плоскости; -виды кривых второго порядка на евклидовой плоскости и их канонические уравнения; -виды поверхностей второго порядка и их канонические уравнения; -понятие линейного оператора и матрицы линейного оператора; -понятие собственного вектора линейного оператора, инвариантного подпространства, методы приведения матрицы линейного оператора к каноническому виду; -понятие евклидова пространства и ортогонального базиса в нем, методы построения ортогональных базисов; -понятие ортогональных подпространств и методы построения ортогональной проекции вектора на заданное подпространство; -виды линейных операторов, действующих в евклидовом пространстве (над полем R и над полем C); -понятия билинейной и квадратичной форм, способы приведения их к каноническому виду; -понятие группы и значение этого понятия в геометрии и физике; Уметь -решать системы линейных уравнений разными способами; -распознавать линейные пространства среди других алгебраических структур; -выяснять линейную зависимость и независимость векторов, находить базис и координаты вектора в данном базисе; -строить сумму и пересечение подпространств; -производить операции над матрицами: складывать, умножать, умножать на число, находить обратную матрицу; -считать определители любого порядка наиболее подходящим методом; - находить скалярное, векторное и смешанное произведения векторов и решать задачи на их применение в геометрии и физике; -записывать уравнения заданного характеристическим свойством множества в выбранной системе координат и исследовать свойства множества по его уравнению; -составлять уравнения прямой линии на плоскости и в пространстве; -записывать уравнение плоскости по элементам ее определяющим; -определять взаимное расположение прямых и плоскостей в пространстве; -составлять уравнения кривых второго порядка по их свойствам и определять вид кривой по заданному уравнению; -распознавать линейный оператор среди других преобразований, находить матрицу линейного оператора, его ядро и образ; -находить собственные векторы линейного оператора, приводить его матрицу к каноническому виду; -строить ортонормированный базис евклидова пространства, находить ортогональные проекции вектора на взаимно ортогональные подпространства; -приводить квадратичную форму к каноническому виду; -приводить к каноническому виду общее уравнение поверхности второго порядка; Иметь навыки -применения векторного и координатного методов в решении геометрических и физических задач; -оперирования с матрицами, определителями, системами линейных уравнений, операторами, действующими в аффинных и евклидовых пространствах.
4. Структура и содержание дисциплины (модуля) Общая трудоемкость дисциплины составляет 5 зачетных единиц, 180 часов.
5. Содержание разделов (тем) дисциплин. Раздел 1. Понятие линейного векторного пространства. 1.1. Понятие вектора в геометрии. Операции над геометрическими векторами. 1.2. Пространство Rn . Линейное пространство однотипных матриц. Раздел 2. Общие системы линейных уравнений. Однородные системы. 2.1. Понятие системы линейных уравнений и ее решения, совместные и несовместные системы, равносильные системы. 2.2. Элементарные преобразования. Правило Жордана-Гаусса исключение переменой из всех управлений, кроме одного. Приведение системы к единичному базису. Общее и частное решения. 2.3. Решение однородной системы. Раздел 3. Линейная зависимость и независимость векторов. Ранг и базис векторов. 3.1. Линейная комбинация векторов. Линейно-зависимые и независимые системы векторов, их свойства. Необходимое и достаточное условие линейной зависимости. 3.2. Линейная зависимость векторов в Rn .Понятие базиса системы векторов. Теорема о двух различных базисах одной и той же системы векторов. 3.3. Ранг системы векторов. Размерность векторного пространства. Координаты вектора относительно данного базиса. Раздел 4. Матрицы. 4.1. Операции над матрицами. Обратная матрица. 4.2. Строчечный и столбцовый ранги матрицы, их поведение при при элементарных преобразованиях матриц. Ранг матрицы. Решение задач на отыскание ранга матрицы, ранга и базиса системы векторов, на разложение вектора по базису. 4.3. Необходимое и достаточное условие совместимости системы линейных уравнений. Базис пространства решений однородной системы линейных уравнений. Раздел 5. Определители. 5.1 Понятие определителя n-го порядка. Свойства определителей . Миноры и алгебраические дополнения. Правило Лапласа разложения определителя по элементам строки (столбца). 5.2. Вычисление определителей некоторых специальных матриц. 5.3. Применение определителей: критерий невырожденности квадратной матрицы. Теорема о базисном миноре, вычисление обратной матрицы через алгебраические дополнения ее элементов, правило Крамера решения системы линейных уравнений. Раздел 6. Элементы векторной алгебры в аналитической геометрии. 6.1.Коллинеарные и компланарные векторы. Базис пространств коллинеарных, компланарных векторов. Понятие координат вектора. Действие над векторами в координатах. 6.2. Специальные произведения векторов: скалярное, векторное, смешанное, двойное векторное, их геометрический смысл, свойства, приложения. Раздел 7. Координатный метод в геометрии. 7.1. Понятие аффинной и прямоугольной декартовой систем координат на плоскости и в пространстве. Координаты точки. 7.2. Решение простейших задач аналитической геометрии в координатах. 7.3. Полярные системы координат на плоскости и в пространстве. Раздел 8. Прямая и плоскость. 8.1. Различные уравнения прямой линии на плоскости и в пространстве: параметрические и канонические ( по точке и направляющему вектору, по двум точкам). Уравнения прямой на плоскости: общее уравнение, уравнение прямой в отрезках, уравнение прямой по точке и угловому коэффициенту, уравнение по точке и нормальному вектору. 8.2. Взаимное расположение двух прямых на плоскости и в пространстве. Геометрический смысл линейных неравенств с двумя переменными. Метрические задачи: угол между прямыми, расстояние от точки до прямой на плоскости и в пространстве. 8.3. Различные уравнения плоскости: параметрические по точке и двум направляющим векторам, по трем точкам, общее уравнение плоскости. Взаимное расположение двух плоскостей и трех плоскостей. Прямая как линия пересечения двух плоскостей. Взаимное расположение прямой и плоскости. 8.4. Метрические задачи на прямую и плоскость: расстояние от точки до плоскости, между двумя скрещивающимися прямыми, угол между двумя прямыми, двумя плоскостями, между прямой и плоскостью. Раздел 9. Кривые и поверхности второго порядка. 9.1. Эллипс, гипербола, парабола, их канонические уравнения и свойства. 9.2. Поверхности вращения. Поверхности вращения второго порядка. 9.3. Эллипсоид, однополостный и двуполостный гиперболоиды, эллиптический и гиперболический параболоиды. Канонически и цилиндрические поверхности. Раздел 10. Подпространства линейного пространства. Изоморфизм векторных пространств. 10.1. Линейное пространство. Базис и размерность линейного пространства. Координаты вектора и их изменение при переходе к новому базису. Изоморфизм пространств. 10.2. Понятие подпространства линейного пространства. Пересечение и сумма подпространств. Базисы пересечения и суммы. 10.3. Прямая сумма подпространств. Линейная оболочка векторов. Раздел 11. Линейные операторы. 11.1. Определение линейного оператора, примеры, простейшие свойства. Матрица линейного оператора. 11.2. Действия с линейными операторами. Изменение матрицы линейного оператора при переходе к новому базису. 11.3. Ядро и образ линейного оператора. Инвариантные подпространства и собственные векторы. 11.4. Приведение матрицы линейного оператора к диагональному виду. Жорданова форма матрицы линейного оператора. Приведение матрицы линейного оператора к Жордановой форме. Раздел 12. Евклидово пространство (вещественное и комплексное). 12.1.Понятие евклидова и унитарного пространств. 12.2. Теорема о существовании ортонормированного базиса. Построение ортонормированных базисов. Ортогональные подпространства и проекции Раздел 13. Линейные операторы, действующие в евклидовом пространстве. 13.1. Линейные функционалы. Оператор, сопряженный к данному. Самосопряженные и унитарные операторы, их свойства. 13.2. Симметрические и ортогональные операторы, действующие в вещественном евклидовом пространстве. Раздел 14. Билинейные и квадратичные формы. 14.1. Понятие билинейной и квадратичной форм. Изменение матрицы билинейной (квадратичной) формы при линейном преобразовании. 14.2. Приведение квадратичной формы к сумме квадратов. 14.3. Закон инерции квадратичных форм. Критерий Сильвестра. 14.4. Общее уравнение кривой и поверхности 2-го порядка, приведение его к каноническому виду. Инварианты кривой. Определение центра и главных направление кривой 2-го порядка. Раздел 15. Элементы теории групп. 15.1. Понятие группы. Группы преобразований. Группа движений евклидовой плоскости. 15.2. Псевдоевклидова плоскость и группа ее движений. Преобразования Лоренца и некоторые следствия из них. . 6. Образовательные технологии: При организации курса используются следующие виды учебной работы: – лекции, практические занятия, консультации, – выполнение двух лабораторных работ, – контрольные и самостоятельные работы, коллоквиумы, – поиск информации на заданную тему в учебниках и специальной литературе по заданию преподавателя, написание небольших рефератов, – выполнение индивидуальных заданий по решению задач 7. Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов
МАТЕРИАЛЫ ТЕКУЩЕГО И ИТОГОВОГО КОНТРОЛЯ ПРОГРАММА ЭКЗАМЕНА ПО КУРСУ "АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА" I семестр 1. Понятие вектора в геометрии. Линейные операции над векторами и их свойства. Понятие линейного векторного пространства. Примеры линейных векторных пространств. Пространство 2. Понятие системы линейных уравнений и ее решения. Совместные и несовместные системы. Определенные и неопределенные системы. Элементарные преобразования системы. Равносильные системы. 3. Правило Жордана-Гаусса исключения переменной из всех уравнений системы кроме одного. Приведение системы к единичному базису. Решение системы линейных уравнений. 4. Однородная система линейных уравнений и свойства ее решений. Связь решений неоднородной системы и соответствующей ей однородной. 5. Линейно зависимые и линейно независимые системы векторов. Необходимое и достаточное условие линейной зависимости векторов. Примеры. 6. Свойства линейно зависимых и линейно независимых систем векторов. Линейная зависимость векторов в 7. Понятие базиса системы векторов. Теорема о двух различных базисах одной и той же системы векторов. Координаты вектора в данном базисе. 8. Ранг системы векторов, его свойства. Размерность векторного пространства. 9. Понятие ранга матрицы. Решение задач по отысканию ранга матрицы. 10. Операции над матрицами, их свойства. Размерность пространства однотипных матриц размера 11. Обратная матрица. Матричная запись системы линейных уравнений и ее решение с помощью обратной матрицы. 12. Понятие определителя квадратной матрицы. Минор и алгебраическое дополнение. Правило Лапласа разложения определителя по элементам какой-либо строки (столбца). 13. Свойства определителей, методы их вычисления. 14. Вычисление обратной матрицы с помощью алгебраических дополнений ее элементов. Правило Крамера решения системы линейных уравнений. 15. Скалярное произведение векторов, его свойства и приложения в геометрии и физике. 16. Векторное произведение векторов, его геометрический смысл, свойства, приложения. 17. Смешанное произведение векторов, его геометрический смысл, свойства, приложения. Двойное векторное произведение. 18. Понятие аффинной и прямоугольной декартовой системы координат на плоскости и в пространстве. Координаты точки. Геометрический смысл координат точки в прямоугольной декартовой системе координат. 19. Полярная система координат, ее связь с прямоугольной декартовой. Сферические и цилиндрические координаты. 20. Различные уравнения прямой линии на плоскости и в пространстве: параметрические уравнения по точке и направляющему вектору, по двум точкам, канонические уравнения. 21. Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов в прямоугольной декартовой системе координат. Уравнение прямой по точке и угловому коэффициенту. 22. Уравнение прямой в отрезках. Уравнение прямой по точке и нормальному вектору в прямоугольной декартовой системе координат. 23. Взаимное расположение двух прямых на плоскости. Расположение прямойотносительно осей координат. 24. Угол между прямыми. Расстояние от точки до прямой на плоскости. 25. Различные уравнения плоскости: параметрические по точке и двум направляющим векторам, трем точкам, общее уравнение плоскости. 26. Взаимное расположение двух и трех плоскостей. Прямая как пересечение двух плоскостей. 27. Взаимное расположение прямой и плоскости, двух прямых в пространстве. 28. Уравнение плоскости по точке и нормальному вектору. Расстояние от точки до плоскости в пространстве. 29. Расстояние от точки до прямой в пространстве. Угол между плоскостями. 30. Эллипс, его каноническое уравнение и свойства. 31. Гипербола, ее каноническое уравнение, свойства. Асимптоты гиперболы. 32. Парабола, ее каноническое уравнение и свойства. 33. Поверхности вращения: эллипсоид, гиперболоиды, параболоид. 34. Канонические уравнения поверхности второго порядка и их исследование методом сечений. 35. Конические и цилиндрические поверхности.
Примерные варианты экзаменационных билетов (I семестр)
Билет № 1 1. Понятие вектора в геометрии; основные характеристики вектора, способы его задания, изображение; равные векторы, свойства отношения равенства векторов. Сложение векторов, свойства операции. 2. Правило Крамера решения системы линейных уравнений. 3. Решить матричное уравнение 4. Написать уравнение перпендикуляра, опущенного из точки Р(-3, 13, 7) на прямую 5. Определить а) вид кривой
Билет № 2 1. Умножение вектора на число, свойства операции. Коллинеарные векторы, необходимое и достаточное условие коллинеарности векторов. Базис системы коллинеарных векторов. Понятие координат вектора относительно базиса. 2. Строчечный и столбцовый ранги матрицы, их неизменность при элементарных преобразованиях матрицы. 3. Вычислить определитель
4. Составить параметрические уравнения проекции прямой 5. Определить а) вид кривой
Билет № 3 1. Компланарные векторы, необходимое и достаточное условие компланарности векторов. Базис системы компланарных векторов. Понятие координат вектора относительно базиса. 2. Теорема о совпадении строчечного и столбцового рангов матрицы. Понятие ранга матрицы. 3. Решить систему методом Жордана-Гаусса
4. Точка А(-3, -5) лежит на гиперболе, фокус которой имеет координаты (-2, -3), а соответствующая директриса дана уравнением 5. Определить а) вид кривой
Билет № 4 1. Теорема о разложении вектора по трем некомпланарным векторам пространства. Понятие базиса системы векторов пространства и координат вектора в нем. Операции над векторами в координатах. 2. Вычисление обратной матрицы с помощью алгебраических дополнений. 3. Вычислить определитель
4. Составить уравнения сторон треугольника, зная одну его вершину С(4, -1), а также уравнения высоты 5. Определить а) вид кривой
Билет № 5 1.Скалярное произведение векторов, его свойства, вычисление по координатам в прямоугольном декартовом базисе, приложения в геометрии и физике. 2. Правило Жордана-Гаусса исключения переменой из всех уравнений кроме одного. Приведение системы к единичному базису. 3. Найти какой-нибудь базис системы векторов и небазисные векторы разложить по базисным 4. Найти ортогональную проекцию точки Р(1, 3, 5) на прямую 5. Определить а) вид кривой
Билет № 6 1. Векторное произведение векторов, его свойства, вычисление по координатам в прямоугольном декартовом базисе, приложения в геометрии и физике. 2. Понятие системы линейных уравнений и ее решения. Совместные и несовместные системы, определенные и неопределенные. Элементарные преобразования системы и их свойство. 3. Определить, являются ли векторы линейно зависимыми; найти ранг системы векторов 4. Найти точку, симметричную точке Р(-13, 4, 6) относительно плоскости, проходящей через прямую 5. Определить а) вид кривой
Билет № 7 1.Смешанное произведение трех векторов, его свойства, вычисление по координатам в прямоугольном декартовом базисе, приложения в геометрии и физике. 2. Однородная система линейных уравнений и свойства ее решений. Связь решений неоднородной системы и соответствующей ей однородной.
4. Найти точку, симметричную точке Р(1, 3, 5) относительно прямой
5. Определить а) вид кривой
Билет № 8. 1. Понятие аффинной и прямоугольной декартовой систем координат на плоскости и в пространстве. Координаты точки относительно системы координат. Решение простейших задач аналитической геометрии в пространстве: вычисление координат вектора по координатам его конца и начала, деление отрезка в данном отношении, координаты центра тяжести системы материальных точек. 2. Понятие обратной матрицы. Необходимое и достаточное условие существования обратной матрицы для квадратной матрицы. 3. Решить систему, используя правило Крамера 4. По данному эксцентриситету 5. Определить а) вид кривой
Билет № 9 1. Полярная система координат, ее связь с прямоугольной декартовой. Сферические и цилиндрические координаты 2. Свойства определителей. 3. Найти все базисы системы векторов: 4.Найти точку, симметричную точке Р (3, -4, -6) относительно плоскости, проходящей через точки М1(-6, 1, -5), М2(7, -2, -1), М3(10, -7, 1). 5.Определить а) вид кривой
Билет № 10 1. Различные уравнения прямой линии на плоскости и в пространстве: параметрические и канонические по точке и направляющему вектору, по двум точкам. 2. Понятие определителя квадратной матрицы. Минор и алгебраическое дополнение элемента. Правило Лапласа разложения определителя по элементам какой-либо строки (столбца). 3. Исследовать и решить систему 4. Гипербола имеет асимптоты 5. Определить а) вид кривой
Билет № 11 1. Общее уравнение прямой линии на плоскости, геометрический смысл его коэффициентов в прямоугольной декартовой системе координат. Уравнение прямой по точке и угловому коэффициенту. 2. Ранг системы векторов, его свойства. Понятие размерности линейного пространства. 3. Решить систему, используя правило Крамера 4. Найти ортогональную проекцию вектора а (14, 2, 5) на прямую 5. Определить а) вид кривой
Билет № 12 1. Уравнение прямой по точке и нормальному вектору. Уравнение прямой в отрезках. 2. Понятие линейного векторного пространства. Пространство Rn как пример линейного пространства, другие примеры линейных пространств. 3. Чему равен ранг матрицы при различных значениях l: 4. Доказать, что прямые 5. Определить а) вид кривой
Билет № 13 1. Взаимное расположение двух прямых на плоскости. Расположение прямой относительно системы координат. Угол между прямыми, лежащими в плоскости. 2. Линейно зависимые и линейно независимые системы векторов, примеры. Необходимое и достаточное условие линейной зависимости векторов. 3. Доказать, что если для матриц А и В оба произведения АВ и ВА существуют, причем АВ = ВА, то матрицы А и В квадратные и имеют одинаковый порядок. 4. Доказать, что прямые 5. Определить а) вид кривой Билет № 14 1. Расстояние от точки до прямой на плоскости. Расстояние между параллельными прямыми. 2. Зависимые и независимые векторы пространства Rn. 3. Доказать утверждение: для того, чтобы квадратная матрица была перестановочна со всеми квадратными матрицами того же порядка, необходимо и достаточно, чтобы эта матрица была скалярной. 4.Даны вершины треугольника АВС: А(1,-1, 2), В(5, -6, 2), С(1, 3, -1). Написать уравнение плоскости, в которой лежит треугольник, и вычислить длину высоты этого треугольника, опущенной из вершины В. 5. Определить а) вид кривой
Билет № 15 1. Различные уравнения плоскости: параметрические по точке и двум направляющим векторам, по трем точкам. Общее уравнение плоскости. 2. Понятие базиса системы векторов. Теорема о двух различных базисах одной и той же системы. 3. Записать систему в матричном виде и решить с помощью обратной матрицы:
4. Составить уравнение эллипса, если его эксцентриситет 5. Определить а) вид кривой
Билет № 16 1. Взаимное расположение двух и трех плоскостей. Прямая, как линия пересечение двух плоскостей. 2. Умножение матриц, свойства операции. 3. Пусть система векторов 4. Составить уравнения сторон треугольника АВС, если даны одна из его вершин В (-4, -5) и уравнения двух его высот 5. Определить а) вид кривой б) вид поверхности
Билет № 17 1. Взаимное расположение прямой и плоскости; угол между прямой и плоскостью. 2. Сложение матриц и умножение матрицы на число, свойства этих операций. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
. .
. и найти его длину.
и найти его длину. ; б) вид поверхности
; б) вид поверхности 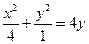
 .
. ,
,  ,
, 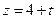 на плоскость
на плоскость  .
.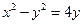 ; б) вид поверхности
; б) вид поверхности 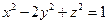
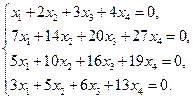
 . Составить уравнение этой гиперболы.
. Составить уравнение этой гиперболы. ; б) вид поверхности
; б) вид поверхности  .
. .
. и медианы
и медианы  , проведенных из одной вершины.
, проведенных из одной вершины.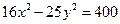 ; б) вид поверхности
; б) вид поверхности  .
. ,
,  ,
,  ,
,  .
.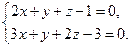
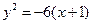 ; б) вид поверхности
; б) вид поверхности 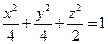 .
. ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
,  и точку О(0, 0, 0).
и точку О(0, 0, 0). ; б) вид поверхности
; б) вид поверхности  .
. 3. Найти матрицу, обратную для матрицы
3. Найти матрицу, обратную для матрицы  .
.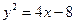 ; б) вид поверхности
; б) вид поверхности  .
.
 определить угол между асимптотами гиперболы.
определить угол между асимптотами гиперболы. ; б) вид поверхности
; б) вид поверхности  .
. ,
,  ,
,  ,
,  .
.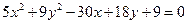 ; б) вид поверхности
; б) вид поверхности  .
.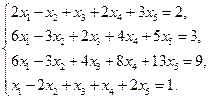
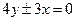 и директрисы
и директрисы  . Написать каноническое уравнение гиперболы.
. Написать каноническое уравнение гиперболы.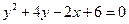 ; б) вид поверхности
; б) вид поверхности  .
.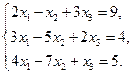
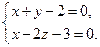
 ; б) вид поверхности
; б) вид поверхности  .
.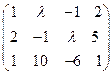
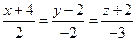 и
и 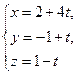 скрещиваются и найти расстояние между ними.
скрещиваются и найти расстояние между ними. . б) вид поверхности
. б) вид поверхности  .
. и
и  параллельны и написать уравнение плоскости, в которой они лежат.
параллельны и написать уравнение плоскости, в которой они лежат.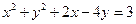 ; б) вид поверхности
; б) вид поверхности  .
. ; б) вид поверхности
; б) вид поверхности  .
.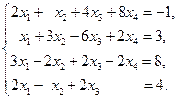
 , фокус F (- 4, 1) и уравнение соответствующей фокусу директрисы
, фокус F (- 4, 1) и уравнение соответствующей фокусу директрисы  .
. ; б) вид поверхности
; б) вид поверхности 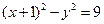 .
. – линейно независима. Является ли линейно независимой система векторов
– линейно независима. Является ли линейно независимой система векторов  ,
,  ,
, 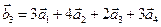 .
. и
и  . Найти длину высоты этого треугольника, опущенную из вершины В.
. Найти длину высоты этого треугольника, опущенную из вершины В. ;
; .
.