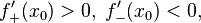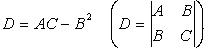|
|
Основные теоремы (без доказательства).2.1.Сформулируйте критерий Коши существования предела функции при x →a . Определение: Пусть a - предельная точка области определения f(x). Говорят, что функция f(x) удовл. в точке a условию Коши, если ∀ ε > 0 ∃ δ > 0, ∀ x' и x'', 0 <x' - a < δ, 0 <x''- a < δ: f(x') - f(x'') < ε. Условие Коши для функции аналогично условию фундаментальности последовательности. Теорема 6.6. (Критерий Коши) Для того, чтобы функция имела предел в точке a, необходимо и достаточно, чтобы она удовлетворяла в этой точке условию Коши. 2.2.Сформулируйте критерий Коши существования предела функции при x → +∞. limx ® ∞(F(x))= A, если " e > 0 $ B(e) >0: " x таких, что |x| > B, выполняется |f(x)-A| < e
2.3. о пределах суммы, разности, произведения и частного двух функций; 1.
2.4.о связи предела функции в данной точке с односторонними пределами в этой точке; Функция f (x) имеет в точке х0 конечный предел тогда и только тогда, когда в этой точкесуществуют конечные правый и левый пределы, и они равны. В этом случае предел функцииравен односторонним пределам
2.5.о первом замечательном пределе; Первый замечательный предел равен
2.6. о втором замечательном пределе; Второй замечательный предел равен
2.7.о непрерывности суммы, разности, произведения и частного двух непрерывных функций; Арифметические операции над непрерывными функциями приводят к непрерывным функциям. Теорема. ! заданные на одном и том же множестве функции f(x) и g(x) непрерывны в точке х0. Тогда функции f(x) ±g(x), f(x)*g(x) и f(x)/g(x) непрерывны в точке х0 (частное условие при g(х0) ≠0) 2.8.Сформулируйте теорему о непрерывности сложной функции; Пусть функция j(t) непрерывна в точке t0 и функция f(x) непрерывна в точке х0=j(t0). Тогда функция f(j(t)) непрерывна в точке t0. 2.9.Сформулируйте теорему о существовании, монотонности и непрерывности обратной функции.
Сформулируйте: 2.1. достаточное условие существования касательной к графику функции y = f (x) в точке ( ( )) 0 0 x , f x ; 2.2.Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке 2.2.теорему о производных суммы, разности, произведения и частного двух функций; ЕОРЕМА 3.Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:
ТЕОРЕМА 4.Производная произведения двух функций равна
ТЕОРЕМА 5. Производная частного двух функций равна
2.3. теорему о производной сложной функции; Пусть y=F(u), где u=j(x), тогда
2.4.теорему о производной обратной функции.
Запишите: 2.5.формулы дифференциалов суммы, разности, произведения и частного двух функций; выще 2.6.формулу для производной функции, заданной параметрически; 2.7. 2.7.формулу n -ной производной произведения двух функций.
2.1.Сформулируйте теорему об интегрировании по частям для неопределенного интеграла.
2.2.Сформулируйте теорему об интегрировании методом замены переменной для неопределенного интеграла
2.3.Перечислите свойства сумм Дарбу. 1)
2)
3)
4)
5)
2.4.Сформулируйте теорему о необходимом и достаточном условии интегрируемости функции f (x)на сегменте [a,b] в терминах нижнего и верхнего интегралов Дарбу.
2.5.Сформулируйте теорему о необходимом и достаточном условии интегрируемости функции f (x)на сегменте [a,b] в терминах нижних и верхних сумм.
2.6.Перечислите известные Вам классы интегрируемых функций. Теорема 1.Если f(x) ограничена на [a, b] и имеет на нем лишь конечное число точек разрыва, то она интегрируема на [a, b]. Теорема 2.Если f(x) монотонна и ограничена на [a, b], то она интегрируема на [a, b]. теорема 3 . Для всякой непрерывной на отрезке [a, b] бла бла бла 2.7.Перечислите свойства определенного интеграла.
Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов
Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла
Свойство 4. Если на отрезке
Свойство 5. Если
Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак
Свойство 7. Для любых трёх чисел
2.8.
2.8. Запишите формулу среднего значения для определенного интеграла и сформулируйте достаточные условия ее применимости. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка С такая, что
Величина Замечание 1. Теорема 2 имеет четкий геометрический смысл: величина определенного интеграла при f(x) ≥ 0 равна площади прямоугольника, имеющего высоту f(C) и основание b - a
2.9. Запишите формулу Ньютона – Лейбница и сформулируйте достаточные условия ее применимости. Если
2.10. Запишите формулу замены переменной для определенного интеграла и сформулируйте достаточные условия ее применимости. Пусть функция 1.определена, непрерывно дифференцируема и монотонна на отрезке 2. 3.функция Тогда
2.11. Запишите формулу интегрирования по частям для определенного интеграла и сформулируйтедостаточные условия ее применимости. если u(x), v(x) - непрерывно дифференцируемые функции, то
непрерыв диффе 2.1. теорему о локальной ограниченности функции, непрерывной в данной точке; 2.2.Пусть функция f:E® R непрерывна в точке a. Тогда f(x) ограничена в некоторой проколотой окрестности точки a. 2.2. теорему об устойчивости знака функции, непрерывной в данной точке; Пусть функция f(x) непрерывна в точке a и f(a)№ 0, то в некоторой окрестности точки a все значения функции положительны или отрицательны вместе с f(a). 2.3. первую теорему Вейерштрасса;
Если функция непрерывна на сегменте, то она ограничена на нем.
2.4. вторую теорему Вейерштрасса; Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения). 2.5.теорему Кантора; Пусть функция f(x) определена и непрерывна на замкнутом отрезке [a,b]. Тогда она равномерно непрерывна на этом отрезке. 2.6. достаточное условие возрастания (убывания) дифференцируемой функции в точке; Для того чтобы функция f (x), дифференцируемая в точке х0 Î (а, b), возрастала (убывала) в точке х0 , достаточно, чтобы f ' (x0) > 0 (f ' (x0) < 0). 2.7. 2.7.теорему Ролля; Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.
2.8.теорему о формуле конечных приращений Лагранжа; Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция
Геометрически это можно переформулировать так: на отрезке
2.9. необходимое и достаточное условие невозрастания (неубывания) дифференцируемой функции на интервале (a,b) ; Для того чтобы дифференцируемая функция f (x) была невозрастающей(неубывающ) на отрезке [а, b], необходимо и достаточно, чтобы её производная f'(x) была неположительной(неотрицательной) на [а, b]. 2.10. достаточное условие возрастания (убывания) дифференцируемой функции на интервале (a,b) ; Если функция f(x), имеющая производную наотрезке [a, b], возрастает на этом отрезке, то ее производнаяна отрезке [a, b] не отрицательна, т. e. f' (x) ≥ 0. 2) Если функция f(x) непрерывна на отрезке [а, b] и дифференцируема в промежутке (a, b), причём f' (x) > 0 для a <x < b, то эта функция возрастает на отрезке [а, b].
2.11. теорему о формуле Коши;
2.12. теорему о формуле Тейлора с остаточным членом в интегральной форме. Пусть в окрестности точки 2.13. Запишите формулу Тейлора с остаточным членом в форме Пеано.
2.14. Запишите формулу Тейлора с остаточным членом в форме Лагранжа
Исследование функций 2.1. о необходимом условии локального экстремума дифференцируемой функции в данной точке; Необходимое условие локального экстремума дифференцируемой функции Если
2.2. о достаточных условиях локального экстремума дифференцируемой функции в окрестности данной точки; Пусть функция
то Заметим, что при этом функция не дифференцируема в точке
2.3. о достаточных условиях локального экстремума дважды дифференцируемой функции в данной точке; Достаточные условия локального экстремума дважды дифференцируемой функции Обозначим Если D > 0, A > 0, то Если D > 0, A < 0, то Если D < 0, экстемума в точке Если D = 0, необходимы дополнительные исследования. 2.15. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


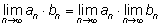
 если
если 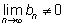
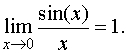
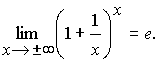



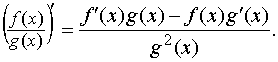
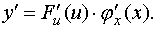









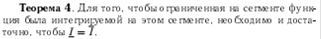

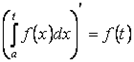
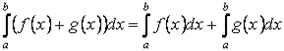
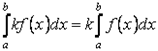
 , где
, где 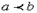 , функции
, функции  и
и  удовлетворяют условию
удовлетворяют условию  , то
, то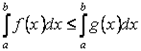
 и
и  - наименьшее и наибольшее значения функции
- наименьшее и наибольшее значения функции  , то
, то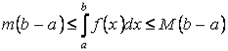
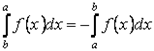
 справедливо равенство
справедливо равенство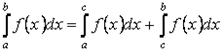
 , что справедливо равенство:
, что справедливо равенство: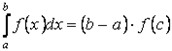
 . (6)
. (6) называется средним значением функции f(x) на отрезке [a, b].
называется средним значением функции f(x) на отрезке [a, b]. непрерывна на отрезке
непрерывна на отрезке  и
и  — ее любая первообразная на этом отрезке, то имеет место равенство
— ее любая первообразная на этом отрезке, то имеет место равенство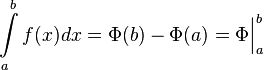
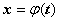
 ,
,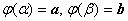 ,
, непрерывна на отрезке [a, b].
непрерывна на отрезке [a, b]. .
.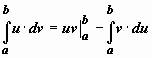 .
. идифференцируема в интервале
идифференцируема в интервале  , то найдётся такая точка
, то найдётся такая точка  , что
, что .
. функция
функция 
 раз дифференцируема и её
раз дифференцируема и её  -я производная интегрируема. Тогда в окрестности точки
-я производная интегрируема. Тогда в окрестности точки  . Эта формула называется формулой Тейлора с записью остатка в интегральной форме.
. Эта формула называется формулой Тейлора с записью остатка в интегральной форме. раз дифференцируема в точке
раз дифференцируема в точке  .
где
.
где  — такая величина, что
— такая величина, что  .
.
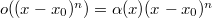 , где
, где  .
Иначе говоря, порядок малости величины слева больше
.
Иначе говоря, порядок малости величины слева больше 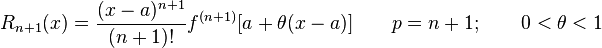
 - точка экстремума функции f, то
- точка экстремума функции f, то и
и  или
или 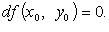
 непрерывна в
непрерывна в  и существуют конечные или бесконечные односторонние производные
и существуют конечные или бесконечные односторонние производные  . Тогда при условии
. Тогда при условии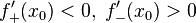
 является точкой строгого локального максимума. А если
является точкой строгого локального максимума. А если