
|
|
Средняя величина коэффициента корреляцииПоскольку коэффициент корреляции в клинических исследованиях рассчитывается обычно для ограниченного числа наблюдений, нередко возникает вопрос о надежности полученного коэффициента. С этой целью определяют среднюю ошибку коэффициента корреляции.
С достаточной для медицинских исследований надежностью о наличии той или иной степени связи можно утверждать только тогда, когда величина коэффициента корреляции превышает или равняется величине трех своих ошибок ( Обычно это отклонение коэффициента корреляции (rxy) к его средней ошибке (mr) обозначают буквой t и называют критериемдостоверности:
Если
Отношение выборочного коэффициента корреляции к свое ошибке является критерием для проверки нулевой гипотезы о равенстве нулю генерального коэффициента корреляции совокупности (или соответственно о независимости случайных вели чин XI и X2):
Число степеней свободы для проверки критерия равно f= n — 2, гипотезу проверяют по таблицам распределения Стьюдента в соответствии с выбранным уровнем значимости. Если вычисленное значение превзойдет или окажется равным соответствующему табличному, нулевую гипотезу отвергают. И в случае малой выборки (число наблюдений меньше 30). Для определения достоверности полученного коэффициента корреляции если t если t Например: имеется коэффициент корреляции, равный +0,72 при числе наблюдений 28.
Полученное tr=35,9 значительно больше табличного t01=2,779, следовательно, полученному коэффициенту корреляции можно доверить с высокой степенью вероятности (>99%).
Приведенная формула для вычисления коэффициента корреляции является параметрической, т.е. предполагает, что анализируемые переменные распределены по нормальному закону. Поэтому перед ее использованием необходимо проверить гипотезу о нормальности обоих распределений. В медико-биологических приложениях часто встречаются случаи, когда характеристики взаимосвязанных структур представляются порядковыми переменными. При этом приходится оперировать так называемыми ранговыми коэффициентами корреляции
Кроме того, такой непараметрический подход применяется в случае малых выборок и если изучаемые выборки не распределены по нормальному закону. Так, например, коэффициент корреляции рангов, предложенный К. Спирменом, вычисляется по формуле:
где di — разность между рангами сопряженных признаков, п — число парных членов ряда. При полной связи ранги признаков совпадут и разность между ними будет равна 0, соответственно коэффициент корреляции будет равен 1. Если же признаки варьируются независимо, коэффициент корреляции получится равным 0. Аналогично коэффициент корреляции рангов является оценкой соответствующего генерального параметра, его значимость оценивается с помощью статистики:
где zа и m связаны соотношениями с уровнем значимости: для а = 5%, z= 1,96 и m = 0,16; для а = 1% z = 2,58, m = 0,69. Нулевую гипотезу отвергают, если полученное значение rs превзойдет или окажется равным рассчитанному критическому значению trs. Таблица 23. Таблица для расчета рангового коэффициента корреляции Спирмена (по данным табл. 2 из примера 1)
Обычно, говоря «коэффициент корреляции», подразумевают коэффициент корреляции Пирсона. При этом важно понимать, что такой коэффициент корреляции удовлетворительно характеризует лишь связи, не слишком отклоняющиеся от прямолинейных (линейная зависимость). А значит, если коэффициент корреляции несущественно отличается от нуля, то это не означает отсутствие связи вообще, это говорит только об отсутствии линейной связи между исследуемыми переменными. Первоначально оценить, к какому типу относится данная связь — прямолинейному или криволинейному, можно, построив эмпирическую линию регрессии. Более точно допустимая степень отклонения связи от прямолинейной определяется при помощи критериев криволинейности. Если изучаемая связь является криволинейной (см. рис. 10, б), силу такой связи можно оценивать с помощью методов, изложенных в справочниках или книгах. Мы хотим обратить внимание читателей на принципиальные ошибки, которые достаточно часто возникают при оценке корреляционных зависимостей. 1)Одна из наиболее распространенных ошибок — отсутствие проверки статистической значимости рассчитанного коэффициента корреляции. Обычной практикой является расчет выборочного коэффициента корреляции (часто по выборкам достаточно малого объема) и в качестве оценки значимости последующее сравнение рассчитанного значения с 0,3. Этот способ некорректен, поскольку статистическая значимость выборочного коэффициента корреляции существенно зависит от объема выборок, по которым он рассчитывается. Часто имеющихся объемов выборок недостаточно для получения статистически значимого выборочного коэффициента корреляции. Надо иметь в виду, что, например, в случае п = 15 даже значение выборочного коэффициента корреляции r= 0,5 окажется статистически незначимым на уровне а = 5%, в то время как при п = 50 меньшее значение коэффициента корреляции r= 0,3 оказывается статистически значимым на том же уровне а. Если соответствующий критерий показал отсутствие значимости оцененного коэффициента корреляции, можно для полученного значения r оценить объем выборки п, достаточный для получения статистически значимого выборочного коэффициента корреляции (т.е. для опровержения нулевой гипотезы об отсутствии корреляции, если корреляция действительно существует):
где величина za задается по принятому уровню значимости (предельной точки распределения Стьюдента, a z ~ преобразование рассчитанного коэффициента корреляции r (формула 58). 2) Однако при обнаружении статистически достоверной корреляции между явлениями часто возникает другая ошибка — желание связать их непосредственной причинной связью. Неверная логическая цепочка выводов при этом приводит к ошибочному заключению: раз явления А и В находятся в тесной корреляционной связи и явление В возникает во времени позднее А, следовательно, А является причиной В. Однако явления А и В могут быть не только не связаны друг с другом причинно-следственной связью, но и не иметь единой первопричины. Пример 12. Изучали зависимость между содержанием вещества В в ткани С и приростом концентрации вещества D в крови у пациентов, получавших препарат А (пример 1, 2-й и 7-й столбцы табл. 2).
Рис. 11. Графическое представление регрессионной зависимости между изучаемыми параметрами для примера 12. По оси абсцисс - содержание вещества В, ммоль/г; по оси ординат - прирост концентрации вещества D, ммоль/л. Для оценки тесноты такой линейной связи рассчитаем коэффициент корреляции (для примера, параметрический, несмотря на малый объем выборок, n = 10). Значение коэффициента корреляции Пирсона, оцененного по (56), равно r = -0,91. Знак «минус» означает, что большим значениям одного признака соответствуют меньшие значения другого. Оценим значимость рассчитанного коэффициента корреляции, значение статистики tr=-6,17. Проверяем данную статистику по таблицам распределения Стьюдента для числа степеней свободы f= 10—2 = 8 и уровня значимости 5%. Рассчитанное значение статистики (tr=- 6,17) по модулю превосходит соответствующее табличное значение (2,31). Таким образом, нулевую гипотезу отвергают на уровне значимости р < 0,05 и рассчитанный коэффициент корреляции признается статистически значимым. В данном случае рассчитанный коэффициент корреляции оказывается статистически высоко значимым (р<0,001). Проверим нулевую гипотезу в отношении r преобразованного коэффициента корреляции. Преобразование Фишера для рассчитанного коэффициента корреляции z= - 1,53; соответствующее значение статистики tz= -4,05. Это рассчитанное значение по модулю превосходит соответствующее табличное 2,31). А значит, вывод о статистической значимости коэффициента корреляции подтверждается (0,001 <р<0,01). Оценим для нашего примера коэффициент корреляции рангов (табл. 23). Если бы отдельные варианты ряда не повторялись, их рангами были бы натуральные числа от 1 в порядке возрастания. Но одинаковым значениям вариант присваиваются ранги, равные средним арифметическим их рангов. Величина di представляет собой попарные разности рангов изучаемых выборок. В качестве правила для проверки правильности ранжирования используют равенство 0 суммы di. Сумма di2 равна 296, по (60) для n = 10 получаем ранговый коэффициент корреляции rs = —0,82. Критическая точка, рассчитанная по формуле (61) для уровня значимости 5% (Za= 1,96; т = 0,16) равна 0,64. Так как значение рангового коэффициента корреляции по модулю превосходит соответствующее критическое значение, с вероятностью более 95% можно утверждать, что между сравниваемыми параметрами существует значимая отрицательная корреляционная связь. Практическая работа При малом числе наблюдений и линейной зависимости между признаками коэффициент корреляции целесообразно рассчитывать, пользуясь следующими формулами: Допустим, сделаны измерения двух признаков
Необходимо установить существует ли связь между изменениями признака Х и Y и если эта связь существует, то какова достоверность связи. (или с какой степенью вероятности можно доверять полученному коэффициенту корреляции). 1. Вычисляем среднее арифметическое для первого признака
для второго признака:
2. Находим сумму квадратов коррилируемых величин (признаков)
3. Находим среднее квадратичное отклонение сопоставляемых величин
4. Находим сумму произведений признака х на признак y
Находим коэффициент корреляции
где x и y – коррелируемые (сопоставляемые) величины.
n – число сравниваемых пар. Приведенные формулы удобны для расчета коэффициентов корреляции при небольшом числе наблюдений (обычно меньше 30-50). Если число наблюдений, велико, то для вычисления коэффициента корреляции целесообразно сначала построить корреляционную таблицу. При этом данные наблюдений, размещенные в таблице, должны быть сгруппированы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ).
).
 , то коэффициент корреляции достоверен, при достаточно большом числе измерений.
, то коэффициент корреляции достоверен, при достаточно большом числе измерений.
 по выбранной вероятности (Р) вычисляют нормированное отклонение t и сравнивают его со значением tP,
по выбранной вероятности (Р) вычисляют нормированное отклонение t и сравнивают его со значением tP,  ( коэффициент Стьюдента (Лобоцкая Н.Л., стр. 343, табл.13, 1973г.) , взятый при
( коэффициент Стьюдента (Лобоцкая Н.Л., стр. 343, табл.13, 1973г.) , взятый при  и выбранной доверительной вероятности Р),
и выбранной доверительной вероятности Р), tP,
tP,  tP,
tP,  ;
; 

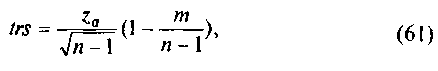

 Прежде всего построили линию регрессии для изучаемых параметров и убедились, что данная зависимость хорошо аппроксимируется прямой, т.е. связь является линейной (рис. 11).
Прежде всего построили линию регрессии для изучаемых параметров и убедились, что данная зависимость хорошо аппроксимируется прямой, т.е. связь является линейной (рис. 11).
 ;
; ;
;




 ;
; коэффициент линейной корреляции
коэффициент линейной корреляции и
и  - средние арифметические признака Х и признака Y
- средние арифметические признака Х и признака Y и
и  - средние квадратичные отклонения сопоставляемых признаков (рядов).
- средние квадратичные отклонения сопоставляемых признаков (рядов).