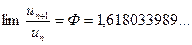|
|
Открытия Пифагора как часть развития эстетической математикиСогласно античной традиции, сам Пифагор установил, что две струны издают благозвучное гармоничное созвучие (консонанс) лишь в случае, когда их длины относятся как целые числа первой четверки: 1 : 2 (октава), 2 : 3 (квинта) и 3 : 4 (кварта). Это открытие было названо законом консонансов.
Закон консонансов впервые облекал в математическую форму физическое явление - звучание струны. Он впервые указывал на существование числовых закономерностей в природе и послужил отправной точкой в развитии пифагорейской философии. Недаром день, когда Пифагор открыл закон консонансов, немецкий физик А.Зоммерфельд назвал днем рождения математической физики. Закон консонансов также впервые открывал эвристические свойства математики и служил первым убедительным свидетельством красоты и гармонии мироздания, мудрой простоты и целесообразности природы, построенной на единых математических принципах. Но закон консонансов стал и выдающимся законом эстетики. Он впервые указывал, что гармония, красота, благозвучие также определяются числом. Причем не просто числом, а простейшей четверкой натуральных чисел 1,2,3,4, которая была названа пифагорейцами четверицей — тетрактис - и почиталась ими как божественное откровение. Так что день открытия Пифагором закона консонансов с полным правом можно назвать и днем рождения экспериментальной эстетики. Знание математических законов строения консонансов открывало дорогу к построению музыкальной шкалы - пифагоровой гаммы - и всей пифагорейской теории музыки. Однако величие Пифагора состояло не только в том, что он открыл закон консонансов, но и сумел оценить его подлинное мировоззренческое значение. Не только «земная» музыка есть гармония и число, но и все мироздание имеет прекрасное, простое и ясное математическое устройство, весь мир есть гармония и число. Так пифагорейцы пришли к своему знаменитому принципу: все есть число. Так мироздание получило имя космос, что по-гречески означает порядок и прекрасное устройство.
Но не менее значимой и непреходящей является и эстетическая сторона идей Пифагора о гармонии мироздания. Мысль о красоте, простоте и гармонии мироздания проходит путеводной нитью по всей истории науки. Не случайно великий физик современности Альберт Эйнштейн писал: «Без веры во внутреннюю гармонию нашего мира не могло бы быть никакой науки. Эта вера есть и всегда останется основным мотивом всякого научного творчества».
Во-первых, пифагорейцы боготворили пентаграмму и выбрали ее в качестве символа приветствия, пожелания здравствования и тайного опознавательного знака. Во-вторых, пентаграмма обладает всеми видами «древних средних», известных пифагорейцам, - это арифметическое, геометрическое и гармоническое среднее - и есть основания считать, что пифагорейцы знали это. В-третьих, - и это самое главное - любые два соседних отрезка пентаграммы относятся в золотой пропорции или, как говорили греки, в крайнем и среднем отношениях. Рассмотрение в пентаграмме любой пары подобных треугольников с отношением сходственных сторон
приводит к квадратному уравнению х2 = а(а - х), которое пифагорейцы легко решали методом «приложения площадей». Решение последнего уравнения и дает
или число φ, которое сегодня благодаря Леонардо да Винчи мы называем коэффициентом золотого сечения. Способы построения правильного пятиугольника (а значит, и пентаграммы) и деления отрезка прямой в крайнем и среднем отношениях как строго научные факты известны сегодня из «Начал» Евклида (кн. IV, пр. 11 и кн. VI, пр. 30 соответственно). Хотя Евклид и жил на 200 лет позже Пифагора, все историки математики единодушны в том, что эти знания восходят к школе Пифагора. По всей вероятности от пифагорейцев золотые пропорции пентаграммы перешли и в греческое искусство. Известно, что прославленный скульптор V в. до н.э. Поликлет, тесно связанный с пифагорейцами, написал теоретический трактат о числовых пропорциях в скульптуре и создал статую «Дорифор» как практическое воплощение своей теории. Трактат Поликлета не сохранился, но «Дорифор», именуемый также «Канон», дошел до нас в римских копиях. Тщательные измерения «Канона» показывают, что единственным правилом, заложенным в нем, могут быть пропорции золотого сечения, а не известные античные системы модульного пропорционирования. Но пропорции золотого сечения присущи даже человеку, как, впрочем, и большинству живых форм на Земле. На связь золотых пропорций пентаграммы и золотых пропорций человека указывает следующее. Древние знали, что человек с максимально раскинутыми руками и ногами вписывается в окружность с центром в пупе человека, при этом сам человек становится очень похож на пентаграмму. В то же время пуп человека является и ключевой точкой в построении золотых пропорций человека. «Это весьма немаловажное обстоятельство способно наводить на большие размышления, - пишет выдающийся знаток античности А.Ф.Лосев - и хотя точных данных к такому пониманию числовой природы канона Поликлета не имеется, все же вероятность его огромна и эстетическая значимость его почти очевидна». Так что знаменитый витрувианский человек Леонардо из галереи Академии Венеции восходит не только к Витрувию, но, возможно, и к Поликлету и даже самому Пифагору. Ученик Платона Аристотель в «Метафизике» пишет: «...заблуждаются те, кто утверждает, что математика ничего не говорит о прекрасном или благом. На самом же деле она говорит прежде всего о нем и выявляет его. Ведь если она не называет его по имени, а выявляет его свойства и отношения, то это не значит, что она не говорит о нем. А важнейшие виды прекрасного - это слаженность, соразмерность и определенность, математика больше всего и выявляет именно их». Хотя средневековье и в религии, и в искусстве явилось антиподом античности, оно продолжило пифагорейскую традицию в онтологии красоты. И на рассвете средневековья один из отцов церкви Блаженный Августин в трактате «О музыке» выступил последовательным пифагорейцем во взглядах на природу красоты: «Число лежит в основе всякого восприятия красоты. Только в том случае, когда само ощущение удовольствия преисполнено определенных чисел, оно способно одобрять равные интервалы и отвергать беспорядочные». И через 1000 лет, на закате средневековья, «последний схоласт» Фома Аквиант в «Сумме теологии» писал: «Красота заключается в должной пропорции: ведь ощущение наслаждается вещами, обладающими должной пропорцией, как ему подобными, поскольку и ощущение есть некое разумение, как и всякая познавательная способность вообще». Заметим, что в утверждении «ощущение есть некое разумение» Фома зорко разглядывает неразрывность правополушарного и левополушарного способов познания действительности. Эпоха Возрождения, провозгласившая себя духовным преемником античности, возродила пифагорейский союз математики и эстетики. С наибольшей ясностью это сделал первый в череде универсальных гениев Возрождения Леон Баттиста Альберти: «Красота есть строгая соразмеренная гармония всех частей, объединяемых тем, чему они принадлежат, - такая, что ни прибавить, ни убавить, ни изменить ничего нельзя, не сделав хуже. Великая это и божественная вещь, осуществление которой требует всех сил искусства и дарования, и редко когда даже самой природе дано произвести на свет что-нибудь вполне законченное и во всех отношениях совершенное...» В 1202 г. итальянский купец Леонардо Пизанский более известный по прозвищу Фибоначчи в «Книге об абаке» впервые смоделировал и решил задачу о развитии популяции кроликов. Рост популяции кроликов описывается знаменитым рядом Фибоначчи, который строится по рекуррентной формуле 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... . Легко заметить, что отношения первых чисел ряда Фибоначчи 1:1, 2:1, 3:2, 5:3, 8:5 есть не что иное, как числовые значения важнейших консонансов примы, октавы, квинты, большой сексты (обращение малой терции 6:5) и малой сексты (обращение большой терции 5:4) соответственно. Также можно обнаружить, что чем больше номер п в отношении двух соседних чисел Фибоначчи, тем ближе это отношение к коэффициенту золотого сечения. Наконец, с помощью разложения числа Ф в цепную дробь получим, что
Так было установлено единство между важнейшими эстетически значимыми пропорциями. Еще через 300 лет в 1509 г. францисканский монах Лука Пачоли в трактате «Divina Proportione» назвал деление отрезка в крайнем и среднем отношении Sectio divina - божественной пропорцией. Пачоли рассмотрел тринадцать свойств божественной пропорции, называя их эпитетами самых превосходных степеней, и по существу провозгласил божественную пропорцию непререкаемым каноном красоты. Друг Пачоли Леонардо да Винчи сделал 60 рисунков к трактату, что в немалой степени способствовало успеху трактата, хотя и предпочитал называть пифагорейскую пропорцию Sectio aurea - золотое сечение. И еще через 300 лет, в середине XIX в., с выходом в свет труда А.Цейзинга «Новое учение о пропорциях человеческого тела», золотое сечение предстало как основной морфологический закон природы и искусства. Эстетико-математическая система Цейзинга может быть сведена к трем основным положениям: золотое сечение господствует в искусстве; золотое сечение господствует в природе; золотое сечение господствует в искусстве именно потому, что оно господствует в природе. Так по прошествии двух тысячелетий вновь зазвучал Аристотелев тезис о подражании искусства природе. Итак, Пифагор и его последователи определили основы взаимосвязи эстетического и математического. Открытие золотого сечения и его пропорций позволило утверждать о существовании эстетической математики.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 Математико-эстетический тезис Пифагора о гармоничном и математическом устройстве мироздания имеет непреходящее значение. Идеи Пифагора вскоре были подхвачены Платоном и сформулированы им в виде важнейшего методологического принципа науки - принципа математизации науки.
Математико-эстетический тезис Пифагора о гармоничном и математическом устройстве мироздания имеет непреходящее значение. Идеи Пифагора вскоре были подхвачены Платоном и сформулированы им в виде важнейшего методологического принципа науки - принципа математизации науки. Вторым математико-эстетическим открытием Пифагора является нахождение золотых пропорций в пентаграмме. Прямых свидетельств о том, что пифагорейцы открыли золотые пропорции в пентаграмме, нет. Однако косвенных указаний достаточно.
Вторым математико-эстетическим открытием Пифагора является нахождение золотых пропорций в пентаграмме. Прямых свидетельств о том, что пифагорейцы открыли золотые пропорции в пентаграмме, нет. Однако косвенных указаний достаточно.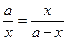
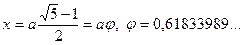
 :
: