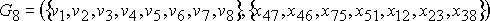|
|
procedure short(n:integer; // количество вершинW:graph; // матрица смежности S,f:integer; // начальная и конечная вершины Var length: integer; // длина пути var Weight:real; // var Path: array[1..NN] of integer); Var v,k,j,m:byte; l:array[1..nn] of real; // метки p1:array[1..nn] of integer; P:integer; // рабочая переменная для вершин H:Set Of byte; // множество вершин, имеющих временные метки Begin H:=[]; // инициализация l For v:=1 to n do begin l[v]:=MaxInt; H:=H+[v];p1[v]:=0; end; l[s]:=0; p:=s; H:=H-[s]; // выбор из Н такой вершины, что значение l минимально while p<>f do begin for v:= 1 to n do If v In H then if w[p,v]<MaxInt then if l[v]> l[p]+w[p,v] then begin l[v]:= l[p]+w[p,v]; p1[v]:=p end; end; m:=f; for v:=1 to n do If v In H then begin if l[m]>l[v] then m:=v end; H:=H-[m]; p:=m; end; // поиск пути Path[1]:=f; length:=2; j:=f; While j<>s Do Begin Path[length]:=P1[j]; j:=P1[j]; length:=length+1 end; For j:=1 to length div 2 Do Begin k:=Path[j]; Path[j]:=Path[length-j]; Path[length-j]:=k; end; length:=length-1; Weight:=l[f];
Задание 1.Имеется 8 городов и матрица стоимостей перевозок между городами. Нарисовать полученный граф. Используя алгоритм Дейкстры, необходимо найти пути минимальной стоимости между городами №1 и №8. Выполнение алгоритма описать пошагово. В результате должен быть представлен сам путь (пути), а не только значение минимальной стоимости.
Пример применения алгоритма Дейкстры
Необходимо найти все кратчайшие пути от вершины №1 для графа, представленого на рисунке
Составим матрицу длин кратчайших дуг для данного графа ∞ 10 18 8 ∞ ∞ 10 ∞ 16 9 21 ∞ ∞ 16 ∞ ∞ 15 ∞ 7 9 ∞ ∞ ∞ 12 ∞ ∞ ∞ ∞ ∞ 23 ∞ ∞ 15 ∞ 23 ∞
Cтартовая вершина, от которой строится дерево кратчайших путей - вершина 1. Задаем стартовые условия: d(1)=0, d(x)=∞ Окрашиваем вершину 1, y=1. Находим ближайшую вершину к окрашенной нами, используя формулу: d(x)=min{d(x); d(y)+ ay,x}
d(2)=min{d(2) ; d(1)+a(1,2)}=min{∞; 0+10}=10 d(3)=min{d(3) ; d(1)+a(1,3)}=min{∞; 0+18}=18 d(4)=min{d(4) ; d(1)+a(1,4)}=min{∞; 0+8}=8 d(5)=min{d(5) ; d(1)+a(1,5)}=min{∞; 0+∞}=∞ d(6)=min{d(6) ; d(1)+a(1,6)}=min{∞; 0+∞}=∞ Минимальную длину имеет путь от вершины 1 до вершины 4 d(4)=8. Включаем вершину №4 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,4)
d(2)=min{d(2) ; d(4)+a(4,2)}=min{10; 8+9}=10 d(3)=min{d(3) ; d(4)+a(4,3)}=min{18; 8+∞}=18 d(5)=min{d(5) ; d(4)+a(4,5)}=min{∞; 8+∞}=∞ d(6)=min{d(6) ; d(4)+a(4,6)}=min{∞; 8+12}=20 Минимальную длину имеет путь от вершины 1 до вершины 2 d(2)=10. Включаем вершину №2 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,2)
d(3)=min{d(3) ; d(2)+a(2,3)}=min{18; 10+16}=18 d(5)=min{d(5) ; d(2)+a(2,5)}=min{∞; 10+21}=31 d(6)=min{d(6) ; d(2)+a(2,6)}=min{20; 10+∞}=20 Минимальную длину имеет путь от вершины 1 до вершины 3 d(3)=18. Включаем вершину №3 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (1,3)
d(5)=min{d(5) ; d(3)+a(3,5)}=min{31; 18+15}=31 d(6)=min{d(6) ; d(3)+a(3,6)}=min{20; 18+∞}=20 Минимальную длину имеет путь от вершины 1 до вершины 6 d(6)=20. Включаем вершину №6 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (4,6)
d(5)=min{d(5) ; d(6)+a(6,5)}=min{31; 20+23}=31 Минимальную длину имеет путь от вершины 1 до вершины 5 d(5)=31. Включаем вершину №5 в текущее ориентированноe дерево, а так же дугу ведущую в эту вершину. Согласно выражению это дуга (2,5)
Мы получили ориентированное дерево кратчайших путей начинающихся в вершине №1 для исходного графа . d(1)=1 Длина маршрута L=0 d(2)=1-2 Длина маршрута L=10 d(3)=1-3 Длина маршрута L=18 d(4)=1-4 Длина маршрута L=8 d(5)=1-2-5 Длина маршрута L=31 d(6)=1-4-6 Длина маршрута L=20
Ориентированное дерево с корнем в вершине №1:
Пример лабораторной работы Вариант 1 (с разбором решения и пояснениями) Задача 1 Выполнить топологическую сортировку для приведенного ниже графа, описав весь ход рассуждений пошагово (процедура сортировки описана ниже):
Procedure ChangeNum; Var head:pt; (*Указатель на начало стека.*) nm,v,i:Integer; t:pt; Begin head:=Nil; nm:=0; (*Текущий новый номер вершины.*) For i:=1 То N Do If Deg[i]=0 Then WriteStack(head,i); (*Первоначальное занесение в стек.*) While Free(head) Do Begin (*Пока стек не пуст. Процедуры WriteStack, ReadStack и функция Free рассмотрены ранее на занятии по стеку.*) ReadStack(head,v); Inc(nm); NewNum[v]:=nm; (*Присваиваем новый номер вершине, выбранной из стека.*) t:=A[v]; While t<>Nil Do Begin (*Просматриваем вершины, связанные с данной.*) Dec(Deg[f.data]); {*Уменьшаем степень этой вершины на единицу.*) If Deg[t^.data]=0 Then WriteStack(head, t^.data); (*Если оказалось, что степень вершины после этого равна нулю, то заносим ее в стек.*) t:=t^.next; (*Переходим к следующей вершине, связанной дугой с данной.*) End; End; End; Решение Рассмотрим трассировку процедуры для указанного графа. Списки смежности: A[1] -> 2 A[2] -> nil A[3] -> 1 6 A[4] -> 1 A[5] -> 3 4 A[6] - > 2 Массив Deg (предполагается, что он формируется отдельной процедурой) Deg[1]=2 Deg[2]=2 Deg[3]=1 Deg[4]=1 Deg[5]=0 Deg[6]=1
Nm=0 1 выполнение цикла Состояние стека: 5 v=5 Состояние стека: nil nm=1, NewNum[5]=1 t-> A[5] Deg[3]=0 Deg[4]=0 Состояние стека: 4 3
2 выполнение цикла Состояние стека: 4 3 v=4 Состояние стека: 3 nm=2, NewNum[4]=2 t-> A[4] Deg[1]=1
3 выполнение цикла Состояние стека: 3 v=3 Состояние стека: nil nm=3, NewNum[4]=3 t-> A[3] Deg[1]=0 Deg[6]=0 Состояние стека: 6 1
4 выполнение цикла Состояние стека: 6 1 v=6 Состояние стека: 1 nm=4, NewNum[6]=4 t-> A[6] Deg[2]=1
5 выполнение цикла Состояние стека: 1 v=1 Состояние стека: nil nm=5, NewNum[1]=5 t-> A[1] Deg[2]=0 Состояние стека: 2
6 выполнение цикла Состояние стека: 2 v=2 Состояние стека: nil nm=6, NewNum[2]=6
Состояние стека: nil Конец цикла.
Массив NewNum (новые номера вершин) NewNum[1]=5 NewNum[2]=6 NewNum[3]=3 NewNum[4]=2 NewNum[5]=1 NewNum[6]=4
Задача 2 Пусть граф задан матрицей смежности:
Построить граф и выполнить обход в глубину. Решение
В качестве вершин последовательно выступают вершины 2,4,6,5,8,9 (в скобках указан также порядок посещения вершин при поиске в глубину). Вершина 9 не имеет смежных с нею непросмотренных вершин. Поэтому из вершины 9 возвращаемся в вершину 6, минуя уже использованные вершины 8,5. Очередной этап начинаем с вершины 6, переходя последовательно в вершины 7,3,13. На следующем этапе в качестве v выступает вершина 1 и из нее осуществляется последовательный переход в вершины 12,10,11
Задача 3 Найти минимальное остовное дерево в неориентированном взвешенном графе, изображенном на приведенном ниже рисунке:
Решение Обозначим ребро, соединяющее вершины vi и vj через xij. Для удобства использования приведенного выше алгоритма решения поставленной задачи, составим матрицу длин ребер. В рассматриваемом графе количество вершин n=8, следовательно, матрица длин ребер графа G будет иметь размерность 8×8 и выглядеть следующим образом:
Согласно приведенному выше алгоритму, выбираем ребро минимальной длины (c47=1) и вместе с инцидентными ему двумя вершинами относим к графу G2. Таким образом, Длина дерева G2 будет равна l(G2)=c47=1. Поскольку
Аналогично находим графы:
Поскольку i=8=n(G), работа алгоритма заканчивается.
Таким образом, искомое минимальное остовное дерево графа G − граф G8, длина которого равна 22.
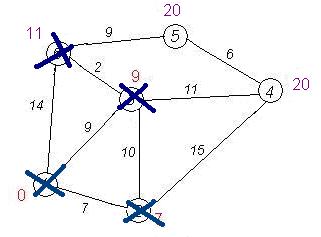
Задача 4 Имеется 6 городов и матрица стоимостей перевозок между городами. Нарисуйте полученный граф. Используя алгоритм Дейкстры, необходимо найти пути минимальной стоимости между городами 1 и всеми остальными горадами. Выполнение алгоритма описать пошагово.
Решение
Примем первоначально значение «бесконечность» за кратчайший путь от вершины 1 до всех остальных вершин.
Определим метки для вершин, смежных с вершиной 1. Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит. Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
Находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7. Пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4. Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем. Ещё один сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется. Следующий сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22<∞, устанавливаем метку вершины 4 равной 22. Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем ее как посещенную.
Следующая вершина для просмотра – вершина 3. Соседями этой вершины являются 2, 4 и 6. Вершина 2 уже помечена как просмотренная. Для вершины 4 получаем путь, равный 9+11=20<22, поэтому помечаем ее новой меткой 20. Для вершины 6 получаем путь, равный 9+2=1<14, поэтому также помечаем ее новой меткой.
Выполняем те же действия для вершины 5. У нее осталась одна непомеченная соседняя вершина – 5. Для этой вершины получаем путь 11+9=20. Обозначаем ее новой меткой.
Следующая вершина по порядку с кратчайшим весом – 4. У нее один непросмотренный сосед – 5. Получаем путь 20+6>20, поэтому метка не меняется. У вершины 5 непросмотренных соседей нет. Поэтому окончательно имеем
Метками обозначены кратчайшие пути до всех вершин от вершины 1.
[1] от adjacency – смежность [2] Поиск в глубину в чистом виде может быть использован, например, для построения дерева подкаталогов. Встаём на корневой каталог, выбираем первый попавшийся подкаталог, далее выбираем в нём какой-либо подкаталог и т.д. пока не доберёмся до пустого (в смысле подкаталогов) каталога. Тогда откатываемся на родительский каталог и выбираем в нём следующий подкаталог, продолжая в нём описанные действия. Как только в каком-либо каталоге просмотрены все подкаталоги, снова откатываемся назад на родительский. К моменту, когда нам придётся откатываться из корневого каталога, мы побываем во всех подкаталогах. Стоит заметить что структура каталогов представляет собой дерево, а поиск глубину работает на любом графе. Он строит дерево в процессе своей работы (дерево поиска в глубину). Представим теперь, что рёбра графа есть коридоры лабиринта, а вершины - комнаты, соединённые этими коридорами. Мы попадаем в начальную комнату, мы умеем помечать комнаты и нам нужно обойти их все. Пометим нашу комнату и будем делать следующее: выбираем первый попавшийся коридор и ходим по нему; если мы попадаем в помеченную комнату, возвращаемся и выбираем следующий по часовой стрелке коридор (пройдя по всем коридорам комнаты, возвращаемся из неё по коридору, по которому в неё пришли), а если нет, то помечаем новую комнату и продолжаем выбирать коридоры указанным способом. Когда мы пройдем по всем коридорам из начальной комнаты, мы точно побываем в каждой комнате лабиринта. [3] или другое объяснение: · находясь в вершине x, нужно двигаться в любую другую, ранее не посещенную вершину (если таковая найдется), одновременно запоминая дугу, по которой впервые попали в данную вершину; · если из вершины x не можем попасть в ранее не посещенную вершину или таковой вообще нет, то возвращаемся в вершину z, из которой впервые попали в x, и продолжаем обход в глубину из вершины z.
[4] Если мы представим, что рёбра есть трубы с одинаковой шириной, то подобное "расползание" очень напоминает распространение воды по трубам если начать эту самую воду равномерно заливать в начальную вершину. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
end;
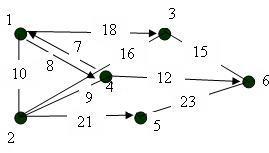
t-> A[2]
.
, продолжаем работу алгоритма. По четвертой и седьмой строкам ищем минимальное число (за исключением использованной единицы) − ребро минимальной длины, инцидентное либо вершине v4, либо v7. Выбираем ребро x46 с длиной c46=3 и вместе с вершиной v6 добавляем к графу G2, обозначая его теперь как G3:
, при этом l(G3)=c47+c46=1+3=4.
, 
