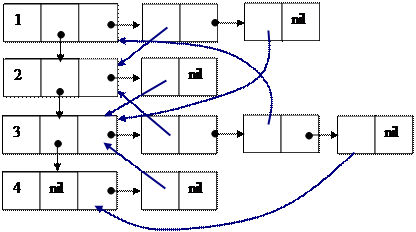
В универсальном динамическом представлении используется линейный список. Для любой вершины можно хранить ее вес.

Например, для графа следующего вида

типы данных для представления графов:

Type refnode=^node;

refarc=^arc;

node=record {список вершин}

id:integer; {номер вершины}

infnode:integer; {вес}

next:refnode; {указатель на следующую вершину в списке}

arclist:refarc {указатель на список дуг}

end;

arc=record {список дуг определенной вершины}

infarc:integer; {вес}

next:refarc; {указатель на следующую дугу, исходящую из данной вершины}

adj:refnode {указатель на вершину, в которую ведет данная дуга}

end;

получим следующее представление:

Задание. Нарисовать списковое представление графа (см. задание 2 раздела «Матрица инцидентности».

Рассмотрим основные процедуры работы с графами.

Основные процедуры работы с графами

Добавление вершины

Процедура AddNode добавляет в граф вершину с заданным номером n и весом x. Предполагается, что уникальность номера обеспечивается вызывающей программой.

Procedure AddNode(Var graph: refnode; n,x:integer);

Var p:refnode;

Begin new(p);

With p^ do

Begin id:=n;

Infnode:=x;

Arclist:=nil;

Next:graph

End;

graph:=p;

end;

Добавление дуги

Процедура добавления дуги AddArc в граф использует в качестве входной информации ссылки на соединяемые вершины и значения вес создаваемой дуги. Обе вершины должны существовать к моменту выполнения процедуры.

Procedure AddArc(u,v:refnode; y:integer);

Var a:refarc;

Beginif u=nil or v=nil then writeln(‘Отсутствует вершина’)

Elsebegin

New(a);

With a^ do begin

Infarc:=y;

Adj:=v;

Next:=u^.arclist

End;

u^.arclist:=a

End

end;

Удаление дуг и вершин

Для удаления дуги указываются две ссылки на вершины, которые эта дуга соединяет. Приведенная ниже процедура удаляет элемент из списка дуг, выходящих из вершины u, если в нем записана ссылка на вершину v. Если таких элементов несколько, то удаляется первый встретившийся.

Procedure DeleteArc(u,v:refnode);

Var a,before:refarc;

Run:boolean;

Begin

If u<>nil thenBegin

a:=u^.arclist;

run:=truel

while a<>nil and run do

if a^.adj=v then run:=false

elsebegin

before:=a;

a:=a^.next

end;

if a<>nil then begin

if a=u^.arclist then u^.arclist:=a^.next

else before^.next:=a^.next;

Dispose(a)

End

End

end;

Процедура удаления вершины более сложная, так как кроме удаления дескриптора вершины и подцепленного к ней списка выходящих дуг, необходимо просмотреть всю оставшуюся часть графа в поисках висячих ссылок. Эти ссылки удаляются с помощью процедуры DeleteArc.

Procedure DeleteNode(Var graph:refnode; v:refnode);

Var before,p,q:refnode;

a,after:refarc;

Begin

p:=graph;

while p<>nil do {цикл по всем вершинам графа}

Begin

q:=p^.next;

if p<>v thenbegin

DeleteArc(p,v) {удаление дуг, направленных удаляемой вершине}

before:=p;

End

elseBegin {удаление вершины v и всех дуг, исходящих из нее}

if p=graph then graph:=q; {если это первая вершина}

a:=p^.arclist;

{удаление списка дуг вершины v}

while a<>nil do

Begin

after:=a^.next;

dispose(a);

a:=after

end;

if p=graph then graph:=q

else before^.next:=q;

dispose(p);

end;

p:=q;

End

end;

Просмотр графа

Просмотр графа заключается в посещении всех вершин и дуг графа и выводе в стандартный файл всей информации о графе. Для непустого графа информация группируется по вершинам (списки смежности).

Procedure BrowseGraph(graph:refnode);

Var a:refarc;

Nn,na: integer; {счетчики количества вершин и дуг}

Begin

Nn:=0; na:=0;

while graph<>nil do

Begin

writeln(‘Вершина ’, graph^.id,’ с весом ’ ,graph^.infnode);

writeln(‘Список дуг:’);

a:=graph^.arclist;

if a=nil then writeln(‘пуст’);

while a<>nil dobegin

writeln(‘Дуга к вершине ’, (a^.adj)^.id,’, вес дуги ’,a^.infarc);

na:=na+1;

a:=a^.next;

end;

nn:=nn+1;

graph:=graph^.next;

end;

writeln(‘В графе ’, nn, ‘вершин и ‘, na,’ дуг’)

end;

Алгоритмы на графах: поиск в глубину и поиск в ширину,

Алгоритм Дейкстры

Обход графов

Просмотр заключается в посещении всех вершин и дуг графа выводе всей информации о графе.

Обход (поиск) в глубину

Метод поиска в глубину (depth first search, DFS) — обобщение метода обхода дерева в прямом порядке.

Обход в глубину[2] (называемый иногда стандартным обходом), есть обход графа по следующим правилам:

1. Добавляет начальную вершину в стек и помечает её как использованную.

2. Рассматривает верхнюю вершину стека и добавляет в стек первую попавшуюся смежную ей неиспользованную вершину, помечая её как использованную. Если такой вершины нет, извлекает вершину стека.

3. Если стек не пуст, переходит к пункту 2.[3]

Таким образом, этот алгоритм обходит все вершины, достижимые из начальной, и каждую вершину обрабатывает не более одного раза.

Текст процедуры обхода в глубину (рекурсивный вариант):

var a:array[1..nmax,1..nmax]of integer;// матрица смежности

used:array[1..nmax]of boolean; // список меток

Не нашли, что искали? Воспользуйтесь поиском по сайту: