|
|
Способы представления графов в памятиДинамические структуры данных. Графы и их представление. Основные операции. Основные понятия теории графов
Графы обычно изображаются в виде геометрических фигур. В классическом графе отсутствуют петли, то есть ребра, соединяющие вершину саму с собой.
Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным (две вершины равноправны, нет никакой разницы между "началом" и "концом" ребра). Чаще всего рассматривают графы, в которых все ребра имеют один тип – либо ориентированные, либо неориентированные. Две вершины v и u называются смежными, если они соединены ребром (дугой) е: e=(v,u). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) - инцидентным соответствующим вершинам. Любому ребру инцидентно ровно две вершины, а вершине может быть инцидентно произвольное количество ребер. Два ребра называются смежными, если они инцидентны одной вершине.
Мультигаф – из одной вершины в другую можно перейти разными способами (граф с кратными ребрами).
Замкнутый путь без повторяющихся ребер называется циклом (или контуром в орграфе); без повторяющихся вершин (кроме первой и последней) - простым циклом. Полнымназывается граф, в котором проведены все возможные ребра. Для графа, имеющего n вершин, таких ребер будет n(n-1)/2. Вершина v достижима из вершины u, если существует путь, начинающийся в u и заканчивающийся в v. Граф называется связным, если все его вершины взаимно достижимы. На рисунке изображен связный граф. Если граф не является связным, то его можно разбить на связные подграфы, называемые компонентами. Компонента связности – это максимальный связный подграф. В общем случае граф может состоять из произвольного количества компонент связности. Любая изолированная вершина является отдельной компонентой связности. Например, в приведённом ниже графе содержится 4 компоненты связности: abhk, gd, c, f.
Взвешенный граф – это граф, некоторым элементам которого (вершинам, ребрам или дугам) сопоставлены числа. Числа-пометки носят названия вес, длина, стоимость. Длина пути во взвешенном графе – это сумма весов ребер (дуг), из которых состоит путь. Способы представления графов в памяти Графический способ представления графов непригоден для вычислительной машины. Поэтому существуют другие способы представления графов.
Пример. Составить матрицу смежности для взвешенного графа: Решение:
Задание 1. Создать матрицу смежности для графа Невзвешенный граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1: Решение:
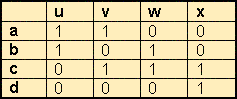
Задание 2. Неориентированный граф задан матрицей смежности. Нарисовать граф. Ответ:
Задание 3. Составить матрицу смежности для следующего графа:
Ответ: Матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа - несимметричной. Удобство матрицы смежности состоит в наглядности и прозрачности алгоритмов, основанных на ее использовании. А неудобство - в несколько завышенном требовании к памяти: если граф далек от полного, то в массиве, хранящем матрицу смежности, оказывается много "пустых мест" (нулей). Матрица инцидентности Матрица инцидентности имеет размер m*n, где n – количество вершин, m – количество дуг графа. Элемент матрицы, соответствующий k-дуге и i-ой вершине, равен · +1, если дуга выходит из вершины; · –1, если дуга входит в вершину · Пример. Для неориентированного графа на рисунке матрица инцидентности:
Задание 1. Составить матрицу инцидентности для следующего графа:
Ответ:
Задание 2. Ориентированный граф заданматрицей инцидентности. Вершины обозначены номерами 1, 2, 3, 4, 5, 6, а ребра латинскими буквами a, b, c, d, e, f, g, h, i.
Нарисовать граф. Ответ:
Список ребер Этот способ задания наиболее удобен для внешнего представления входных данных. Каждая строка входного файла содержит информацию об одном ребре или дуге в следующем виде: <номер начальной вершины> <номер конечной вершины> [<вес ребра>] Например, для следующих графов получим списки:
Списки смежности Этот способ задания графов подразумевает, что для каждой вершины будет указан список всех смежных с нею вершин (для ориентированного графа – список вершин, являющихся концами исходящих дуг): <номер начальной вершины>: <номера смежных вершин> Пример: (рис. графов см. выше) 1) a: b c b: c d f c: d f d: f 2) a: b 1 c 10 b: a 1 c 2 d 10 c: a 10 d 3 d: b 10 c 3 Этот способ представления графов является внутренней реализацией списка смежности: в одном линейном списке содержатся номера начальных вершин, а в остальных – списки исходящих из них дуг. Введем следующие типы данных для представления графов: Type refnode=^node; refarc=^arc; node=record {список вершин} id:integer; {номер вершины} infnode:integer; {вес} next:refnode; {указатель на следующую вершину в списке} arclist:refarc {указатель на список дуг} end; arc=record {список дуг определенной вершины} infarc:integer; {вес} next:refarc; {указатель на следующую дугу, исходящую из данной вершины} adj[1]:refnode {указатель на вершину, в которую ведет данная дуга} end; 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Граф (graph) – объект, состоящий из множества кружков (точек) и множество соединяющих их линий. Кружки (точки) называются вершинами графа (nodes), линии со стрелками – дугами (arcs), без стрелок – ребрами (edges). Т.е. граф – это пара G=(V,E), где V - множество вершин, а E - семейство пар реберei=(vi1, vi2), vij принадлежит V. Вершины графа можно использовать для представления объектов, а дуги — для отношений между объектами.
Граф (graph) – объект, состоящий из множества кружков (точек) и множество соединяющих их линий. Кружки (точки) называются вершинами графа (nodes), линии со стрелками – дугами (arcs), без стрелок – ребрами (edges). Т.е. граф – это пара G=(V,E), где V - множество вершин, а E - семейство пар реберei=(vi1, vi2), vij принадлежит V. Вершины графа можно использовать для представления объектов, а дуги — для отношений между объектами. Граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным (орграф). В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Пример: G=(V,E): V={1, 2, 3, 4, 5}; E={(1,2), (1,5), (3,1), (5,2), (5,3), (5,4)}.
Граф, в котором направление линий принципиально (линии являются дугами) называется ориентированным (орграф). В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги (дуга из нее исходит), вторая - концом дуги (дуга в нее входит). Пример: G=(V,E): V={1, 2, 3, 4, 5}; E={(1,2), (1,5), (3,1), (5,2), (5,3), (5,4)}. Степенью вершиныв неориентированном графе называется число инцидентных ей ребер. Для ориентированного графа различают исходящую степень, определяемую как число выходящих из него ребер, и входящую степень,определяемую как число входящих в нее ребер. Сумма исходящей и входящей степеней называется степенью вершины. Изолированная вершина – это вершина со степенью 0 (нуль-граф).
Степенью вершиныв неориентированном графе называется число инцидентных ей ребер. Для ориентированного графа различают исходящую степень, определяемую как число выходящих из него ребер, и входящую степень,определяемую как число входящих в нее ребер. Сумма исходящей и входящей степеней называется степенью вершины. Изолированная вершина – это вершина со степенью 0 (нуль-граф). Путем называется последовательность вершин v1, v2, …, vn, для которой существуют ребра (или дуги в орграфе) v1 ® v2, v2 ® v3, ..., vn-1 ® vn. Этот путь начинается в вершине v1 и, проходя через вершины v2, v3, ..., vn-1, заканчивается в вершине vn. Длина пути— количество дуг (ребер), составляющих путь, в данном случае длина пути равна n – 1. Путь называется простым, если все вершины на нем, за исключением, может быть, первой и последней, различны. Для неориентированного графа на рис.рисунка путями будут adbc и abc.
Путем называется последовательность вершин v1, v2, …, vn, для которой существуют ребра (или дуги в орграфе) v1 ® v2, v2 ® v3, ..., vn-1 ® vn. Этот путь начинается в вершине v1 и, проходя через вершины v2, v3, ..., vn-1, заканчивается в вершине vn. Длина пути— количество дуг (ребер), составляющих путь, в данном случае длина пути равна n – 1. Путь называется простым, если все вершины на нем, за исключением, может быть, первой и последней, различны. Для неориентированного графа на рис.рисунка путями будут adbc и abc.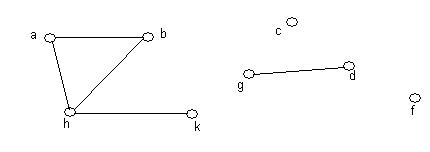
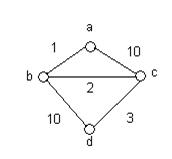 Матрица смежности – это матрица n×n, где n - число вершин. Строка с номером i содержит 1 в строке с номером j, если существует дуга из вершины i в вершину j.
Матрица смежности – это матрица n×n, где n - число вершин. Строка с номером i содержит 1 в строке с номером j, если существует дуга из вершины i в вершину j. Небольшое затруднение возникнет в том случае, если в графе разрешаются ребра с весом 0. Тогда придется хранить два массива: один с нулями и единицами, которые служат показателем наличия ребер, а второй - с весами этих ребер.
Небольшое затруднение возникнет в том случае, если в графе разрешаются ребра с весом 0. Тогда придется хранить два массива: один с нулями и единицами, которые служат показателем наличия ребер, а второй - с весами этих ребер.

 и нули во всех остальных строках.
и нули во всех остальных строках.