
|
|
При равноускоренном подъеме грузаДИНАМИЧЕСКОЕ ДЕЙСТВИЕ НАГРУЗОК Напомним, что, в отличие от статических нагрузок, динамические нагрузки существенно изменяются во времени. Возникающие при динамическом нагружении деформации системы также с течением времени изменяются. При этом перемещения частиц системы происходят с ускорениями, что приводит к возникновению инерционных сил, которые необходимо учитывать в расчетах. Поскольку природа и спектр динамических нагрузок достаточно широки, выделим только те ее виды, которые характерны для строительных конструкций и сооружений. Виды динамических нагрузок 1. Инерционнаянагрузкавызывается ускорениями системы, постоянными по направлению. 2. Вибрационная нагрузка представляет собой нагрузку, периодически переменную по величине и направлению. Возникающие при этом периодически переменные ускорения, а следовательно и инерционные силы, обусловливают вибрацию системы. Опасным при вибрационном нагружении является режим резонанса. 3. Ударные неподвижныенагрузки возникают в системе при падении на нее различных грузов (например, при падении молота на наковальню). 4. Подвижныенагрузки отличаются тем, что изменяют место своего расположения на конструкции (например, движущийся по мосту транспорт). 5. Сейсмическиенагрузки представляют собой колебания и удары земной коры, которые передаются к конструкции. Очевидно, что расчет конструкций при динамическом нагружении является более сложным, чем при статическом приложении нагрузки. Наиболее просто решаются задачи при инерционной нагрузке. Для решения таких задач используется кинетостатический метод, суть которого сводится к приведению задачи динамики к задаче мгновенного статического равновесия, что осуществляется на основе принципа Даламбера.
Инерционные нагрузки Здесь и в дальнейшем характеристики напряженного и деформированного состояния конструкции при динамическом нагружении будем называть динамическими и обозначать нижним индексом «дин». Рассмотрим вопросы определения динамического напряжения и формирования условия прочности при инерционной нагрузке на примере двух конкретных задач.
I. Динамические напряжения в тросе и условие прочности для троса при равноускоренном подъеме груза Рассмотрим задачу определения динамических напряжений в тросе при равноускоренном подъеме груза, а также сформулируем условие прочности для троса. Схема подъема груза приведена на рис. 1. Стрелками указаны направления движения груза (v) и направление ускорения (а). Считаем заданными:
Для определения динамических напряжений ( Уравнение равновесия для действующей системы сил имеет вид
Отсюда получаем
Заметим, что в последнем выражении (1) соотношение, записанное в первых скобках, представляет собой напряжение, возникающие в тросе от действия веса груза и веса троса, т. е. напряжения при статическом приложении соответствующих нагрузок (σст)
Подставляя (2) в (1), получим
Обозначим
тогда динамические напряжения в тросе
Очевидно, что
Сформируем условие прочности для троса. В общем случае, как и при статическом нагружении, условие прочности при динамическом приложении нагрузки имеет вид
Здесь [σдин] – допускаемое значение динамических напряжений. При инерционной нагрузке величину [σдин] принимают равной основным допускаемым напряжениям для материала ([σдин]= [σ]). Максимальные динамические напряжения в тросе формально определяются выражением
Максимальные статические напряжения будут возникать при положении груза на исходном нижнем (нулевом) уровне, а опасное сечение будет располагаться при х = l
Максимальное значение коэффициента динамичности определяется максимальной величиной ускорения при подъеме груза (a=amax)
Подставляя приведенные выше выражения в (4), получим условие прочности в тросе при равноускоренном подъеме груза
На основе условия (5) можно решать достаточно широкий круг задач. Во-первых, выполнить проверочный расчет (при всех заданных характеристиках троса, груза и движения проверить прочность троса). Выполнить ряд проектировочных расчетов – определить максимальные (допустимые): высоту подъема – l, площадь сечения троса – A, вес груза – G, ускорение подъема – amax (естественно, при заданных остальных параметрах). Необходимая для подъема груза сила (
Очевидно, что при этом 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 – ускорение, с которым поднимается груз;
– ускорение, с которым поднимается груз;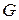 – вес груза;
– вес груза;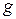 – ускорение свободного падения;
– ускорение свободного падения;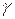 – удельный вес материала троса;
– удельный вес материала троса;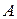 – площадь сечения троса;
– площадь сечения троса; – максимальная длина троса.
– максимальная длина троса. Рис.1
Рис.1
 Рис.2
Рис.2
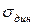 ), возникающих в тросе, используем метод сечений в сочетании с принципом Даламбера и строим расчетную схему метода сечений (рис.2). В центре тяжести груза и части троса (длиной х), наряду с силами веса груза (G) и троса (γ·А·x), согласно принципу Даламбера, прикладываем силы инерции, направленные противоположно ускорению и равные произведению массы на ускорение: для груза –
), возникающих в тросе, используем метод сечений в сочетании с принципом Даламбера и строим расчетную схему метода сечений (рис.2). В центре тяжести груза и части троса (длиной х), наряду с силами веса груза (G) и троса (γ·А·x), согласно принципу Даламбера, прикладываем силы инерции, направленные противоположно ускорению и равные произведению массы на ускорение: для груза –  , для троса –
, для троса –  . Полагаем, что динамические напряжения в плоскости поперечного сечения троса распределены равномерно.
. Полагаем, что динамические напряжения в плоскости поперечного сечения троса распределены равномерно. .
. (1)
(1) . (2)
. (2) .
. ,
, . (3)
. (3) является безразмерной величиной, которая указывает во сколько раз динамические напряжения в тросе больше статических. Называют эту величину коэффициентом динамичности.
является безразмерной величиной, которая указывает во сколько раз динамические напряжения в тросе больше статических. Называют эту величину коэффициентом динамичности. . (4)
. (4) .
. .
. .
. . (5)
. (5) ), при заданных значениях: l, A, G и a, определяется выражением
), при заданных значениях: l, A, G и a, определяется выражением .
. .
.