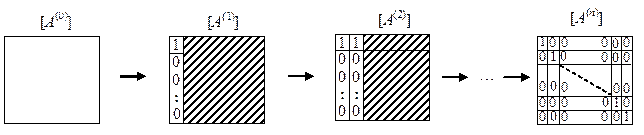|
|
Алгоритм метода Гаусса без обратного хода (схема Жордана)РЕШЕНИЕ УРАВНЕНИЙ СОСТОЯНИЯ МЕТОДОМ ГАУССА
Практически в основе всех прямых методов решения линейных алгебраических уравнений установившегося режима электрической системы лежит метод последовательного исключения неизвестных, называемый методом Гаусса. К числу наиболее характерных вычислительных схем этого метода относятся алгоритмы с обратным ходом и без обратного хода.
Алгоритм метода Гаусса с обратным ходом Решение системы
по этому алгоритму состоит из двух этапов. На первом этапе(прямой ход) исходная система за На втором этапе(обратный ход) последовательно определяются значения неизвестных от
Последовательность операций, выполняемых при прямом ходе, следующая: На первом шаге в исходной системе уравнений:
первое уравнение делится на
где для элементов первой строки
для элементов нижележащих строк
Выполнение операций первого шага требует, чтобы элемент Второй шаг состоит в исключении Третий и последующие шаги выполняются аналогично. Формулы для расчета коэффициентов системы уравнений на произвольном (k-ом) шаге запишутся:
На последнем шаге (
и их отличие от нуля является условием осуществления процесса вычислений. Процесс преобразования матрицы коэффициентов
В результате выполнения
На этапе обратного хода определяются неизвестные в следующем порядке. Поскольку
В общем виде формулы для обратного хода могут быть записаны как:
Алгоритм метода Гаусса без обратного хода (схема Жордана) Решение системы На первом шаге вычисления выполняются точно так же, как и в алгоритме Гаусса с обратным ходом. Получаемая в результате этого преобразования система уравнений
характеризуется тем, что первый элемент первого столбца матрицы равен единице, а остальные элементы столбца равны нулю. На втором шаге, как и в предыдущем алгоритме, в качестве ведущего элемента выбирается диагональный элемент второго столбца матрицы Выполнение операций произвольного k-го шага соответствует преобразованию k-го столбца таким образом, чтобы его диагональный элемент Формулы для расчета коэффициентов системы уравнений на k-ом шаге будут иметь точно такой же вид, как и в алгоритме метода Гаусса с обратным ходом, отличаясь лишь диапазоном изменения индекса строки i, поскольку на каждом шаге рассчитываются элементы всех строк матрицы
В результате выполнения последнего шага ( Процесс преобразования матрицы коэффициентов

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 линейных алгебраических уравнений вида
линейных алгебраических уравнений вида
 до
до 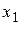 .
.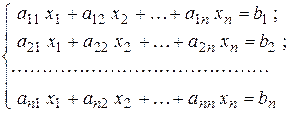
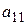 . После этого коэффициент при
. После этого коэффициент при 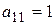 . Далее
. Далее 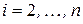 ) путем умножения первого уравнения каждый раз на
) путем умножения первого уравнения каждый раз на 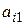 и вычитанием из
и вычитанием из  - го уравнения. В результате этих операций получается система уравнений с матрицей коэффициентов
- го уравнения. В результате этих операций получается система уравнений с матрицей коэффициентов 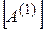 :
: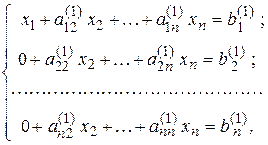
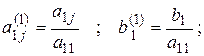
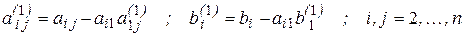 .
.
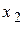 из системы уравнений
из системы уравнений  , полученной на первом шаге путем выполнения аналогичных операций при использовании в качестве ведущего элемента
, полученной на первом шаге путем выполнения аналогичных операций при использовании в качестве ведущего элемента 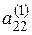 . В результате система приводится к виду
. В результате система приводится к виду 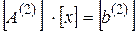 .
.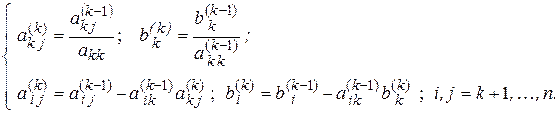
 ) второе из выражений (2-5) определяет
) второе из выражений (2-5) определяет  . Таким образом, при прямом ходе ведущими последовательно выступают элементы:
. Таким образом, при прямом ходе ведущими последовательно выступают элементы: ,
,
 исходной системы уравнений к верхней треугольной на этапе прямого хода проиллюстрируем графически, выделяя области, соответствующие пересчитываемым на последующих шагах элементам, штриховкой:
исходной системы уравнений к верхней треугольной на этапе прямого хода проиллюстрируем графически, выделяя области, соответствующие пересчитываемым на последующих шагах элементам, штриховкой: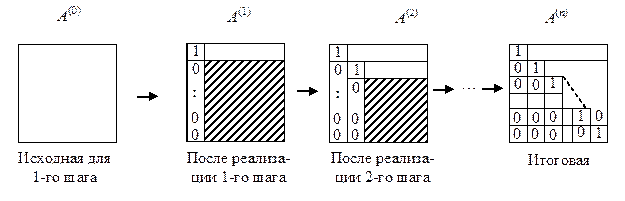

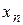 уже определён, записываем:
уже определён, записываем: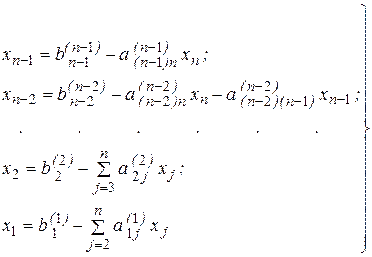
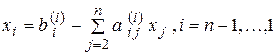
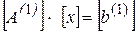
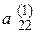 . Отличие состоит в том, что дополнительно преобразуется также и первая строка матрицы
. Отличие состоит в том, что дополнительно преобразуется также и первая строка матрицы  , причем таким образом, чтобы элемент
, причем таким образом, чтобы элемент  обратился в нуль.
обратился в нуль.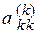 стал равен единице, а недиагональные элементы
стал равен единице, а недиагональные элементы  – нулю.
– нулю. . Следовательно, на k-ом шаге элементы матрицы
. Следовательно, на k-ом шаге элементы матрицы 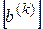 определяются по выражениям:
определяются по выражениям:
 и все элементы столбца
и все элементы столбца 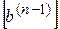 , получаем матрицу
, получаем матрицу 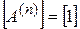 и, следовательно,
и, следовательно, 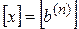 .
.