
|
|
УСТАНОВИВШЕГОСЯ РЕЖИМА ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ
Линейные алгебраические уравнения, встречающиеся при решении задачи расчета установившихся режимов, имеют следующие характерные особенности: · в подавляющем большинстве случаев матрица коэффициентов системы уравнений является слабо заполненной, т.е. содержит большое число нулевых элементов. Так число ненулевых элементов в матрице узловых проводимостей для сложных схем замещения электрических систем с большим количеством узлов составляет примерно · диагональные элементы матрицы · при использовании линейных узловых уравнений (2.2) и линеаризованных нелинейных уравнений (2.4) матрица коэффициентов системы симметрична. Учет этих особенностей при реализации метода Гаусса на ЭВМ позволяет существенно повысить вычислительную эффективность программы за счет сокращения требуемого объема памяти и времени расчета. Учет слабой заполненности матрицы Однако при выполнении шагов прямого хода метода Гаусса в матрице Если рассматривать один k-й шаг прямого хода метода Гаусса, то наименьшее возрастание заполненности будет в том случае, когда k-я строка матрицы Учет доминирования диагональных элементов матрицы. При решении системы линейных алгебраических уравнений последовательность нумерации уравнений и неизвестных выбирается на основании условий сохранения слабой заполненности матрицы [А] в процессе расчета и обеспечения заданной точности решения. Условие обеспечения точности решения выполняется при применении схемы главного элемента. В общем случае последовательность нумерации уравнений, определяемая каждым из указанных условий, может быть различной. Опыт решения электроэнергетических задач показывает, что в связи с доминированием диагональных элементов матрицы [А] с точки зрения обеспечения высокой точности расчетов, как правило, допустима любая нумерация уравнений, не изменяющая состава ее диагональных элементов, т.е. перестановка двух строк должна сопровождаться перестановкой тех же столбцов. Поэтому нумерацию уравнений и неизвестных можно выполнять только по условию учета слабой заполненности матрицы [А]. Учет симметричности матрицы [А]. В тех случаях, когда матрица [А] симметрична, можно дополнительно уменьшить требуемый объем памяти ЭВМ и вычислений, используя алгоритм метода Гаусса с обратным ходом. Возможность такой экономии определяется тем, что квадратный блок матрицы [А(k)], пересчитываемый на каждом шаге прямого хода, с элементами Действительно согласно (2-5)
и если квадратный блок матрицы [А(k-1)] с элементами Следовательно, при симметричной матрице [А] достаточно оперировать только с ее верхней или нижней треугольной частью, что значительно сокращает как объем памяти, так и количество вычислений. Зададимся конкретным порядком матрицы [А] и оценим объем оперативной памяти необходимой для хранения полной матрицы при различных формах организации ее размещения в памяти ЭВМ. Число ненулевых элементов для системы со 100 узлами оценивается: При организации хранения в памяти ЭВМ такой матрицы в виде классического двухмерного массива необходимы три ячейки памяти на один элемент матрицы. В ячейках размещаются индексы строки, столбца и численное значение элемента, т.е. общая потребность в памяти для хранения матрицы [А] При организации хранения в памяти ЭВМ матрицы [А] в форме вектора: n2+1, где 1 – число элементов в строке двумерного массива, суммарная потребность в памяти сокращается до значения 20 001 ячейка. Учет слабой заполненности матрицы [А] позволяет сократить объем сохраняемой информации при организации хранения в форме вектора (адрес и значение) до величины порядка:
Учет симметричности позволяет также сократить объем хранимой информации: число ненулевых элементов на главной диагонали – n в силу симметричности, нулевые элементы распределены равномерно над и под главной диагональю:
из них не нулевых Таким образом, при организации хранения информации в форме вектора для сохранения полной информации о матрице [А] с учетом слабой заполненности достаточно сохранить значения:
ненулевых элементов. С учетом 250 ячеек адресов и 1 ячейки размерности матрицы итого 501 ячейка памяти против 30 000. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , т.е.
, т.е. 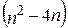 элементов этой матрицы равны нулю;
элементов этой матрицы равны нулю; ненулевые и обычно по абсолютной величине превосходят недиагональные элементы соответствующей строки (или столбца);
ненулевые и обычно по абсолютной величине превосходят недиагональные элементы соответствующей строки (или столбца); появляются новые ненулевые элементы, т.е. ее заполненность возрастает. Это, во-первых, существенно усложняет программу и, во-вторых, может свести на нет возможную экономию памяти и времени расчета, связанную с учетом слабой заполненности исходной матрицы
появляются новые ненулевые элементы, т.е. ее заполненность возрастает. Это, во-первых, существенно усложняет программу и, во-вторых, может свести на нет возможную экономию памяти и времени расчета, связанную с учетом слабой заполненности исходной матрицы 
 также будет симметричным.
также будет симметричным. ;
;
 ;
;

 симметричен, то
симметричен, то  .
. . При суммарном числе элементов 10 000 число нулевых элементов составляет
. При суммарном числе элементов 10 000 число нулевых элементов составляет  .
. .
. - число элементов под диагональю
- число элементов под диагональю .
.