
|
|
РЕШЕНИЕ УРАВНЕНИЙ СОСТОЯНИЯ ИТЕРАЦИОННЫМИ МЕТОДАМИ
Итерационные методы решения систем линейных алгебраических уравнений позволяют получить значения искомых неизвестных в результате многократного выполнения единообразных шагов вычислений, называемых последовательными приближениями или итерациями. В отличие от прямых методов, к числу которых относится метод Гаусса, решение можно получить только с заданной конечной точностью, причем с увеличением требуемой точности растет и количество итераций. В итерационном процессе матрица коэффициентов В связи с этим итерационные методы по вычислительной эффективности уступают методу Гаусса, особенно при построении алгоритма с учетом слабой заполненности матрицы Рассмотрим два итерационных метода решения систем линейных алгебраических уравнений – метод простой итерации и метод Зейделя. Эти методы допускают простое обобщение на решение нелинейных уравнений установившегося режима, связывающих мощности и напряжения в узлах электрической системы. При этом многие свойства итерационного процесса решения нелинейных уравнений установившегося режима электрической системы можно объяснить, рассмотрев более простой случай – решение линейных уравнений состояния. Метод простой итерации. Исходная система линейных алгебраических уравнений:
в предположении, что
По методу простой итерации система уравнений (2-13) решается следующим образом: 1) задаются начальными (нулевыми) приближениями неизвестных 2) значения 3) подстановкой полученных значений Таким образом, на k-ом шаге итерационного процесса система (2-13) запишется как:
Итерационный процесс продолжается до тех пор, пока значения
Для выполнения этого условия при любой заданной точности решения, т.е. при любом сколь угодно малом значении
где При выполнении условия (2-16) для произвольного начального приближения Для выяснения условий, определяющих сходимость итерационного процесса по методу простой итерации, запишем уравнение в матричной форме. Исходная система уравнений
приводится к виду (2-13) путем введения матрицы
и выполнения следующих преобразований:
Умножим уравнение слева на матрицу
В соответствии с введенными обозначениями математическая формулировка итерационного процесса (2-14) в матричной форме записи будет иметь вид:
откуда следует, что
Поскольку это выражение справедливо для любых
Для сходимости итерационного процесса, условием которого служит матричное соотношение
при любом столбце начальных приближений
В теории существуют методы, определяющие необходимые и достаточные условия сходимости итерационного процесса. Однако на практике используют более простые достаточные условия сходимости. При анализе сходимости решения систем линейных алгебраических уравнений используются три легко вычисляемые нормы матрицы
Для сходимости процессов простой итерации и метода Зейделя при решении систем линейных уравнений при любом начальном приближении достаточно, чтобы любая из указанных норм матрицы была меньше единицы. Несоблюдение любого из достаточных условий ещё не значит, что итерационный процесс расходится. Выполнение же любого из этих условий означает, что методы простой итерации и Зейделя сходятся. К сожалению, для линейных уравнений узловых напряжений достаточные условия сходимости методов простой итерации и Зейделя не выполняются и приходится использовать более сложные методы.
Метод Зейделя Этот метод, так же как и метод простой итерации, базируется на использовании уравнений, приведенных к виду (2-13). Однако, в отличие от метода простой итерации, для вычисления
Если достаточные условия, общие для обоих итерационных методов, выполняются, то процесс по методу Зейделя сходится, причем быстрее, чем по методу простой итерации, т.е. при одинаковых начальных приближениях неизвестных и одинаковой заданной точности решение по методу Зейделя получается за меньшее число итераций. Таким образом, как метод Зейделя, так и метод простой итерации не всегда обеспечивает возможность получения решения, поскольку расходимость соответствующих итерационных процессов не исключена. При этом условия сходимости (или расходимости) определяются только свойствами матрицы В заключение отметим, что итерационные методы решения систем линейных алгебраических уравнений широко применялись тогда, когда объем оперативной памяти ЭВМ являлся определяющим ограничением размерности задачи при расчете установившегося режима электрической системы. Развитие средств вычислительной техники с одной стороны, и разработка эффективных алгоритмов метода Гаусса с учетом слабой заполненности матрицы

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
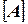 линейной системы уравнений не подвергается преобразованиям, что позволяет максимально использовать её слабую заполненность. Это, в свою очередь, приводит к меньшему объему вычислений на каждой итерации по сравнению с каждым шагом метода Гаусса. Однако общее число итераций может оказаться (и, как правило, оказывается) значительно больше порядка
линейной системы уравнений не подвергается преобразованиям, что позволяет максимально использовать её слабую заполненность. Это, в свою очередь, приводит к меньшему объему вычислений на каждой итерации по сравнению с каждым шагом метода Гаусса. Однако общее число итераций может оказаться (и, как правило, оказывается) значительно больше порядка 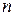 решаемой системы уравнений.
решаемой системы уравнений.
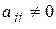 при
при  , приводится к виду:
, приводится к виду: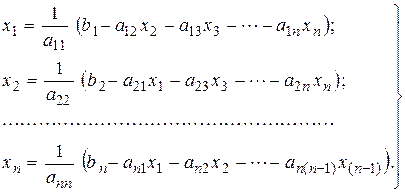
 ;
; подставляются в правые части уравнений (2-13) и тем самым определяются следующие приближения неизвестных
подставляются в правые части уравнений (2-13) и тем самым определяются следующие приближения неизвестных  ;
; находится следующее приближение и т.д.
находится следующее приближение и т.д.
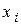 , полученные на двух смежных итерациях, не будут отличаться на величину, меньшую заданной погрешности решения
, полученные на двух смежных итерациях, не будут отличаться на величину, меньшую заданной погрешности решения 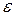 , т.е. до выполнения условия:
, т.е. до выполнения условия: .
.
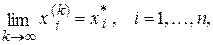
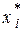 - точное решение исходной системы уравнений.
- точное решение исходной системы уравнений.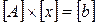
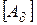 :
: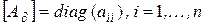

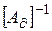
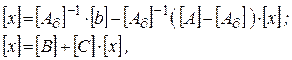
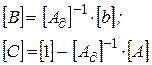
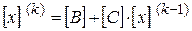

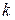 , то, очевидно, его можно записать как
, то, очевидно, его можно записать как
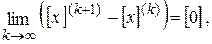
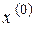 необходимо, чтобы
необходимо, чтобы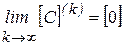 .
.
 :
: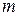 - норма матрицы – равна наибольшей из сумм абсолютных величин элементов одной строки матрицы;
- норма матрицы – равна наибольшей из сумм абсолютных величин элементов одной строки матрицы; - норма матрицы - равна наибольшей из сумм абсолютных величин элементов одного столбца матрицы;
- норма матрицы - равна наибольшей из сумм абсолютных величин элементов одного столбца матрицы; -й переменной на
-й переменной на 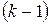 -ом шаге, так и на данном. При этом на
-ом шаге, так и на данном. При этом на 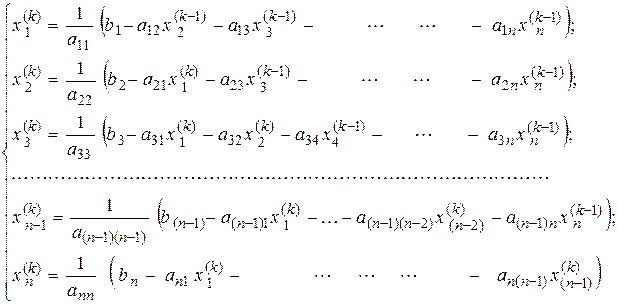
 и не зависят ни от начального приближения, ни от столбца правых частей
и не зависят ни от начального приближения, ни от столбца правых частей 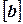 . Последние два фактора влияют лишь на количество итераций, необходимых для получения решения с заданной точностью.
. Последние два фактора влияют лишь на количество итераций, необходимых для получения решения с заданной точностью.