
|
|
Общие теоремы динамики механической системы
Разработаны некоторые общие приемы изучения движения механической системы, которые позволяют получить важные характеристики движения без интегрирования (78).
Теорема о движении центра масс механической системы
Теорема: Центр масс механической системы движется как материальная точка, наделенная массой всей системы, в предположении, что все внешние силы приложены в центре масс системы.
При решении задач необходимо спроектировать (79) на координатные оси
Из рассмотрения уравнений (79) и (80) вытекает закон сохранения движения центра масс системы: Если сумма всех внешних сил системы равняется нулю, то центр масс ее движется с постоянной по величине и направлению скоростью или покоится
Другими словами, скорость центра масс нельзя изменить действием внутренних сил системы. Частным случаем выполнения закона (81) является равенство нулю суммы проекций сил на одну из координатных осей, в этом случае центр масс вдоль этой оси не перемещается или движется с постоянной скоростью.
Теорема об изменении количества движения Механической системы Количеством движения системы называют геометрическую сумму количеств движения всех материальных точек системы
Для выяснения физического смысла (82) вычислим производную от (72)
Решая совместно (82) и (83), получим
Таким образом, вектор количества движения механической системы определяется произведением массы системы на скорость ее центра масс. Теорема: Производная по времени от вектора количества движения системы равна геометрической сумме всех внешних сил системы.
При решении задач уравнение (85) необходимо спроектировать на координатные оси:
Из анализа (85) и (86) вытекает следующий закон сохранения количества движения системы: Если сумма всех сил системы равна нулю, то вектор количества движения ее сохраняет свою величину и направление. Если В частном случае этот закон может выполнять вдоль одной из координатных осей. Если Теорему об изменении количества движения целесообразно использовать в тех случаях, когда в систему входят жидкие и газообразные тела.
Теорема об изменении кинетического момента механической системы
Количество движения характеризует только поступательную составляющую движения. Для характеристики вращательного движения тела введено понятие главного момента количеств движения системы относительно заданного центра (кинетического момента). Кинетическим моментом системы относительно данного центра называется геометрическая сумма моментов количеств движения всех его точек относительно того же центра
Кинетический момент тела относительно осей равен произведению момента инерции тела относительно этой оси на угловую скорость тела
Из (90) следует, что кинетический момент характеризует только вращательную составляющую движения. Характеристикой вращательного действия силы является ее момент относительно оси вращения. Теорема об изменении кинетического момента устанавливает взаимосвязь между характеристикой вращательного движения и силой, вызывающей это движение. Теорема: Производная по времени от вектора кинетического момента системы относительно некоторого центра равна геометрической сумме моментов всех внешних сил системы относительно того же центра
При решении инженерных задач (91) необходимо спроектировать на координатные оси
Их анализа (91) и (92) вытекает закон сохранения кинетического момента: Если сумма моментов всех внешних сил относительно центра (или оси) равна нулю, то кинетический момент системы относительно этого центра ( или оси) сохраняет свою величину и направление.
Кинетический момент нельзя изменить действием внутренних сил системы, но за счет этих сил можно изменить момент инерции, а следовательно угловую скорость.
Теорема об изменении кинетической энергии Механической системы
Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех ее материальных точек
Вычисление кинетической энергии твердого тела Поступательное движение Как известно, при поступательном движении скорости всех точек тела в один и тот же момент времени равны, тогда (93) можно представить в виде
При поступательном движении тела, его кинетическая энергия равна половине произведения массы на квадрат скорости центра масс. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (79)
. (79) . (80)
. (80)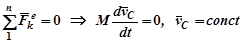 . (81)
. (81) . (82)
. (82)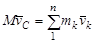 . (83)
. (83)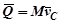 . (84)
. (84) . (85)
. (85) . (86)
. (86) , то
, то  , Q=const. (87)
, Q=const. (87) , то, Qz=const. (88)
, то, Qz=const. (88) . (89)
. (89) . (90)
. (90)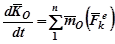 . (91)
. (91) . (92)
. (92) ,или
,или 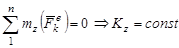
 . (93)
. (93) . (94)
. (94)