
|
|
Момент силы относительно точки (центра)
Момент силы относительно точки это количественная характеристика вращательного эффекта от действия силы. Моментом силы относительно точки называется величина, равная взятому с соответствующим знаком произведению модуля силы на плечо, т.е. кратчайшее расстояние от центра до линии действия силы.
Если сила стремится повернуть тело относительно точки против часовой стрелки, то момент положительный, если по часовой стрелке – отрицательный. При решении задач для вычисления момента силы в некоторых случаях удобно пользоваться следующей теоремой Вариньона о моменте равнодействующей. Теорема: Момент равнодействующей плоской сходящейся системы сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Пара сил
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары. Расстояние между линиями действия сил пары называется плечом пары. Пара сил не имеет равнодействующей. Действие пары на тело сводится к некоторому вращательному эффекту, числено характеризуемому моментом пары сил. Моментом пары сил называется величина, равная взятому с соответствующим знаком произведению модуля одной из силы пары на ее плечо
Свойства пары сил 1. Действие пары сил на тело не изменится, если у нее произвольным образом изменить силы и плечо при неизменном моменте пары. 2. Не изменяя действия пары сил, ее можно переносить произвольным образом в плоскости ее действия. 3. Пару сил можно повернуть в плоскости ее действия на любой угол. 4. Действие нескольких пар сил, приложенных в одной плоскости, можно заменить одной парой сил, момент которой равен алгебраической сумме моментов заданных пар сил.
Условие равновесия плоской системы сил Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на оси координат и алгебраическая сумма моментов всех сил относительно любой точки равнялись нулю
Кинематика
Кинематика – это раздел теоретической механики, в котором изучается движение тел без учета действия сил, вызывающих или поддерживающих это движение.
Основные определения Движением тела называется изменение его положения в пространстве по отношению к заданной системе отсчета. Системой отсчета называется любое тело, по отношению к которому изучается движение. Время в механике считается независимой переменной, одинаковой для всех наблюдателей. В отдельных случаях при изучении движения некоторых тел, их можно принять за геометрические точки, пренебрегая размерами, например, когда расстояние, проходимое телом, значительно больше его размеров. Это позволяет значительно упростить изучение характеристик движения.
Кинематика точки Для изучения движения тела это движение нужно каким-либо образом задать, т.е. задать положение тела (точки) относительно данной системы отсчета в любой момент времени.
Способы задания движения
1. Естественный способ задания движения Этим способом удобно пользоваться, когда известна траектория движения точки.
При естественном способе задания движения должны быть заданы: 1. Траектория движения точки 2. Начало отсчета дуговой координаты 3. Направление отсчета 4. Закон движения точки по траектории в виде
2. Векторный способ задания движения
(15) - уравнение движения точки в векторной форме Геометрическое место концов вектора (годограф вектора) определяет траекторию движения точки. 3. Координатный способ задания движения В этом случае, в отличие от естественного способа, траектория заранее не известна. Задается система отсчета Oxyz и координаты материальной точки как функции времени
(16) - уравнения движения материальной точки в координатной форме. Уравнение траектории можно получить в явном виде. Для этого надо исключить из уравнений (16) время.
Скорость точки
Скоростью точки называется векторная величина, характеризующая быстроту изменения положения материальной точки в пространстве с течением времени.
Определение скорости при векторном способе задания движения.
Средняя скорость точки равна отношению приращения радиус-вектора к соответствующему приращению времени. Значение скорости в заданный момент времени
Вектор скорости материальной точки в данный момент времени равен первой производной от радиус-вектора точки по времени. Вектор скорости всегда направлен по касательной к траектории точки в заданный момент времени. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
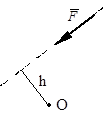
 . (10)
. (10) ,
,  . (11)
. (11) Пара сил - это система двух равных по модулю, параллельных и направленных в противоположные стороны сил.
Пара сил - это система двух равных по модулю, параллельных и направленных в противоположные стороны сил. . (12)
. (12) . (13)
. (13) Траекторией называется линия, которую описывает материальная точка при ее движении в пространстве.
Траекторией называется линия, которую описывает материальная точка при ее движении в пространстве. (14)
(14)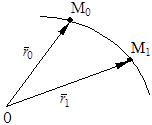 В этом случае для определения положения материальной точки в пространстве в любой момент времени нужно задать начало отсчета (точка О) и зависимость радиус-вектора от времени
В этом случае для определения положения материальной точки в пространстве в любой момент времени нужно задать начало отсчета (точка О) и зависимость радиус-вектора от времени (15)
(15) (16)
(16) Рассмотрим точку в двух положениях M0 и M1.
Рассмотрим точку в двух положениях M0 и M1.  - приращение времени,
- приращение времени, - приращение радиус-вектора,
- приращение радиус-вектора, . (17)
. (17) . (18)
. (18)