
|
|
Методика расчета переходного процесса в линейной электрической цепи классическим методом.3.2.1. Составить систему уравнений на основе законов Кирхгофа, описывающих состояние цепи после коммутации, и исключением переменных получить одно дифференциальное уравнение. Для простых цепей получается дифференциальное уравнение первого или второго порядка, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе. При составлении уравнений пользуются следующими соотношениями:
3.2.2. Составить общее решение полученного дифференциального уравнения цепи в виде суммы частного решения неоднородного дифференциального уравнения и общего решения соответствующего однородного дифференциального уравнения. Применительно к электрическим цепям в качестве частного решения неоднородного дифференциального уравнения выбирают установившийся режим в рассматриваемой цепи. Токи и напряжения установившегося режима обозначают iу и иу. Общее решение однородного дифференциального уравнения описывает процесс в цепи без источников ЭДС и тока, который называют свободным процессом.Токи и напряжения свободного процесса обозначают iсв и uсв Таким образом, искомый ток или напряжение имеет вид
Далее все выкладки будут приведены на примере тока, а для напряжений получаются аналогичные выражения. 3.2.3. Ток установившегося режима iу определяется любым из ранее изученных методов расчета, т.к. предыдущие занятия были посвящены методам расчета установившихся режимов линейных электрических цепей. 3.2.4. Свободный ток будет иметь вид: Для нахождения корней, число которых равно порядку однородного дифференциального уравнения, характеристического уравнения p воспользуемся простейшим методом: - составим выражение полного комплексного сопротивления для послекоммутационной цепи Z(jω). - заменим в данном выражении jω на p и приравняем полученное выражение к нулю; - из характеристического уравнения Z(p) = 0 найдем искомое p. 3.2.5. Для нахождения постоянных интегрирования A, число которых равно порядку однородного дифференциального уравнения, найдем независимые начальные условия iL(0), uC(0), используя которые, решим уравнение (1) для t = 0. При этом делаем допущение, что ключи идеальны, т.е. коммутация происходит мгновенно без учета возможных искровых и дуговых явлений. 3.2.6. В качестве ответа записывают полученную по выражению (1) функцию i(t) и её график в диапазоне от нуля до (3…5)τ, где
3.3. Задание для самостоятельного расчета переходного процесса классическим методом. На рисунке 3.3 представлена схема для расчета переходного процесса, а в таблице 3.1 варианты заданий по схеме. R0 = 2 Ом. В таблице указаны положения ключей К1 и К2 до коммутации и после коммутации. Если ключ К2 и до, и после коммутации разомкнут (положение «0»), то ветвь с сопротивлением Z3 можно убрать из варианта. Если ключ К1 до и после коммутации не находился в положении «2», то ветвь с сопротивлением Z1 можно не изображать. Если в столбце φ0 задан угол, то е0=Emsin(314t+φ0), а в столбце е0 в этом случае задано Em. Если φ0 не задано, то е0 - источник постоянной ЭДС. Рассчитать и построить iL(t), uC(t) iС(t), uL(t), если соответствующие элементы есть в схеме. Сделать вывод о надежности схемы, если предельно-допустимые кратковременные значения токов равны 10∙Iраб, а напряжений 5∙Uраб. Iраб, Uраб – это максимальные значения токов (напряжений) в установившемся режиме при замкнутом положении ключа.
Таблица 3.1
Примечания: варианты 1-24 – первый порядок постоянного и переменного тока; варианты 25-46 – второй порядок постоянный и переменный ток; варианты 47-50 – особый случай (отключение двух однотипных элементов).
Список рекомендуемой литературы 1. Касаткин А.С. Электротехника: учеб. для неэлектротехн. спец. вузов / А.С. Касаткин, М.В. Немцов. - 11-е изд., стер. - М.: Академия, 2007. - 539 с. 2. Борисов Ю.М. Электротехника: Учеб. для неэлектротехн. спец. вузов / Ю. М. Борисов, Д. Н. Липатов, Ю. Н. Зорин. - 2-е изд., перераб., и доп. - М. : Энергоатомиздат, 1985. 3. Электротехника: Учеб. для неэлектротехн. спец. вузов / [Зейдель Х.Э. и др.]; Под ред. В.Г. Герасимова. - М. : Высш. шк., 1985. - 480 с. 4. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: [Учеб. для втузов] / Л. А. Бессонов. - 9-е изд. - М.: Гардарика, 2002. - 638с. 5. Рекус Г.Г. Сборник задач по электротехнике и основам электроники: Учеб. пособие для вузов по неэлектротехн. спец. / Г.Г. Рекус, А.И. Белоусов. - 2-е изд., перераб. - М.: Высш. шк., 2001. - 416с.
ЭЛЕКТРОТЕХНИКА
Методические указания к практическим занятиям для студентов всех форм обучения неэлектротехнических специальностей
Составители: Квон Алексей Михайлович; Автайкин Илья Николаевич
Компьютерная верстка А.М. Квон ______________________________________________ Подписано в печать Формат 60х84/16 Бумага офсетная Офсетная печать Печ. л. 2,56. Изд. № Усл. печ. л. 2,56. Тираж экз. Уч.-изд. л. 1,09. Заказ № Цена руб. ______________________________________________ Кубанский государственный технологический университет 350072, г. Краснодар, ул. Московская, 2, кор. А

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  ,
,  .
. ,
,  . (1)
. (1) .
. - постоянная времени переходного процесса.
- постоянная времени переходного процесса. . (2)
. (2) . (3)
. (3)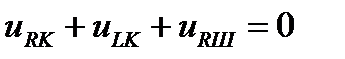 и переписать его в комплексной форме
и переписать его в комплексной форме  . Т.к. E – источник постоянной ЭДС, то ω = 0, следовательно и XК = ωLК = 0. По той же причине далее будем записывать не комплексный ток, а действующее значение тока
. Т.к. E – источник постоянной ЭДС, то ω = 0, следовательно и XК = ωLК = 0. По той же причине далее будем записывать не комплексный ток, а действующее значение тока  . Таким образом, iКу=0.
. Таким образом, iКу=0.
 . Найдем p – корень из характеристического уравнения
. Найдем p – корень из характеристического уравнения  . Для чего составим выражение полного комплексного сопротивления Z(jω) для послекоммутационной цепи:
. Для чего составим выражение полного комплексного сопротивления Z(jω) для послекоммутационной цепи:  , заменим jω на p и приравняем к нулю, получим характеристическое уравнение
, заменим jω на p и приравняем к нулю, получим характеристическое уравнение  , откуда
, откуда  с-1.
с-1.
 , то найдем ток через индуктивность до коммутации iК(0-), который примем за iК(0). До коммутации (до размыкания ключа) был установившийся режим (см. рис. 3.1), поэтому
, то найдем ток через индуктивность до коммутации iК(0-), который примем за iК(0). До коммутации (до размыкания ключа) был установившийся режим (см. рис. 3.1), поэтому  . Т.к. E – источник постоянной ЭДС, то ω = 0, следовательно и XК = ωLК = 0. Следовательно,
. Т.к. E – источник постоянной ЭДС, то ω = 0, следовательно и XК = ωLК = 0. Следовательно,  А, т.е. iК(0) = 12 А. Теперь используя выражение (4) для t = 0 находим A: iК(0) = iКу(0) + iКсв(0) → 12 = 0 + А∙е -1001∙0 → А = 12.
А, т.е. iК(0) = 12 А. Теперь используя выражение (4) для t = 0 находим A: iК(0) = iКу(0) + iКсв(0) → 12 = 0 + А∙е -1001∙0 → А = 12.
 или
или  .
Второй вариант проще:
uК=iК∙RШ=1000∙12∙е -1001∙t = 12000∙е -1001∙t В. (5)
Постоянная времени
.
Второй вариант проще:
uК=iК∙RШ=1000∙12∙е -1001∙t = 12000∙е -1001∙t В. (5)
Постоянная времени  с. Строим графики зависимостей iК(t), uК(t) на интервале 0-5τ.
с. Строим графики зависимостей iК(t), uК(t) на интервале 0-5τ.
