|
Метод эквивалентного генератора
1.5.1 Подписать узлы, расставить произвольно направления токов в ветвях и подписать токи.
1.5.2 Элементы нагрузочной ветви подписать как Ен, Rн, Iн.
1.5.3 Преобразовать заданную схему в стандартную схему эквивалентного генератора с нагрузочной ветвью и записать для нее выражение искомого тока нагрузки вида
 . .
1.5.4 Основная цель метода – получить выражение Iн = f(Rн), но для этого необходимо найти Еэ и Rэ. Для нахождения Еэ необходимо отключить нагрузочную ветвь (режим холостого хода) и найти напряжение на ее зажимах.
1.5.5 Для нахождения Rэ отключить нагрузочную ветвь и закоротить все источники ЭДС, а затем найти общее сопротивление цепи относительно зажимов нагрузки.
1.5.6 В качестве ответа:
– записать выражение вида
 , ,
где вместо Еэ и Rэ записать рассчитанные в п. п. 1.5.4, 1.5.5 значения;
– построить зависимость Iн = f(Rн), причем диапазон изменения Rн задать таким образом, чтобы он включал заданное значение Rн.
| Пример расчета методом эквивалентного генератора
| | выполняем п. 1.5.1
| выполняем п. 1.5.2
| |
|
Нагрузочной принята 3-я ветвь
| | выполняем п. 1.5.3
| Составим стандартную схему эквивалентного генератора с нагрузкой.
На схеме сохраняем направление тока как в предыдущем пункте, т.е. от узла «a» к узлу «b».
Выражение искомого тока
 .
Так как в нагрузочной ветви отсутствует источник, то Ен не записываем. .
Так как в нагрузочной ветви отсутствует источник, то Ен не записываем.
| | выполняем п. 1.5.4
| | Убираем из схемы нагрузочную ветвь (3-я ветвь) и находим напряжение на ее зажимах (напряжение Uab). Рекомендуется убрать из схемы лишние токи (ток I2).
Для нахождения Еэ можно использовать любой из выше представленных методов, например, метод непосредственного применения законов Кирхгофа.
По 2-му закону Кирхгофа для «контура 1»  , откуда , откуда  . В последнем выражении неизвестна величина I1, которую найдем по 2-му закону Кирхгофа из «контура 2» . В последнем выражении неизвестна величина I1, которую найдем по 2-му закону Кирхгофа из «контура 2»  , откуда , откуда
 . .
| | выполняем п. 1.5.5
| После отключения нагрузочной ветви и закорачивания источников ЭДС получим следующую схему для нахождения Rэ
Откуда
 . .
| | выполняем п. 1.5.6
| Предположим, в результе расчетов по п.п. 1.5.4 и 1.5.5 получили Еэ = 8 В, Rэ = 4 Ом, а Rн = R3 = 6 Ом было задано, тогда ответ получим в виде
  , А , А
При Rн = 6 Ом получим Iн = 0,8 А.
|
1.6 Варианты заданий для самостоятельного решения
На рисунке 1.3 приведен скелет расчетной электрической цепи, содержащей 13 ветвей, а в таблице 1 указаны исходные данные. Если в ячейке указано два числа, то первое – это сопротивление ветви, а второе – ЭДС той же ветви. Сопротивление ветви может быть равно нулю, тогда прилегающие к ней узлы объединяются, или бесконечности, в таком случае соответствующая ветвь не изображается на расчетной схеме.
Таблица 1 – Исходные данные к рисунку 1.3
| Вариант
| Состав ветвей схемы
| |
|
|
|
|
|
|
|
|
|
|
|
|
| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| R/Е,

| |
| 12/60
| 10/10
|
|
| ∞
| ∞
|
|
|
| ∞
|
| 2/15
|
| |
| 2/60
|
| 2/15
|
| 6/20
| ∞
| ∞
| ∞
|
|
|
|
|
| |
| 2/80
|
| 8/15
|
| ∞
| ∞
| 8/15
|
|
| ∞
|
|
|
| |
| 4/80
|
| 6/15
|
|
|
| ∞
| ∞
|
|
| ∞
| 4/12
|
| |
| 4/60
|
|
|
| ∞
| ∞
| 4/12
| ∞
|
|
|
| 10/12
|
| |
| ∞
| 6/24
|
|
| ∞
|
|
|
|
| ∞
| 8/80
|
| 2/20
| |
|
| 6/10
| ∞
|
|
| 6/12
| ∞
| ∞
|
|
| 6/60
|
| ∞
| |
| 5/50
| 5/15
| ∞
|
|
|
|
| ∞
|
|
| ∞
| 6/15
| ∞
| |
| 6/40
| 6/5
|
|
| ∞
| ∞
| 6/10
|
|
| ∞
|
|
|
| |
|
|
| 2/12
|
| 2/10
| ∞
| ∞
| ∞
|
|
| 4/40
|
|
| |
| 8/60
| 4/10
|
|
| ∞
| ∞
|
|
|
| ∞
|
| 10/15
|
| |
| 6/80
|
| 12/20
| 2/10
|
| ∞
| ∞
| ∞
|
|
|
|
|
| |
|
|
|
|
| ∞
| ∞
|
| 8/12
|
| ∞
| 8/60
|
| 4/15
| |
|
|
|
|
|
| ∞
| ∞
| ∞
| 2/12
| 2/12
| 6/60
|
|
| |
| 4/40
|
| 2/12
|
| ∞
| ∞
|
| 2/8
|
| ∞
|
|
|
| |
| ∞
| 0/10
|
|
|
|
| ∞
| ∞
|
| 4/5
| 3/45
|
|
| |
| 8/80
|
|
|
| ∞
| ∞
| 2/10
|
|
| ∞
|
|
|
| |
|
|
| 10/8
| ∞
|
| ∞
|
|
| ∞
|
| 4/60
|
| 2/16
| |
| 2/40
|
| 2/8
| 4/10
|
| ∞
| ∞
| ∞
|
|
|
|
|
| |
| 4/60
| 2/15
|
|
| ∞
| ∞
|
|
|
| ∞
|
|
|
| |
| 2/40
| 2/10
| 2/10
|
|
| ∞
| ∞
| ∞
|
|
|
|
|
| |
| 4/60
|
| ∞
|
|
| ∞
| 12/15
| ∞
|
|
|
| 6/15
| ∞
| |
| ∞
|
| ∞
|
|
| 8/80
| 12/10
| ∞
|
| 8/12
|
|
| ∞
| |
| 2/60
|
| ∞
|
|
| ∞
|
| ∞
|
|
|
| 12/10
| ∞
| |
| 6/20
|
| ∞
| ∞
|
|
|
| ∞
| 5/15
|
| 4/50
|
| ∞
| |
| 4/40
|
| ∞
| 5/40
|
| ∞
| ∞
|
|
|
|
|
| 6/40
| |
| 2/50
|
| ∞
| 5/50
| 8/50
|
|
| ∞
| ∞
|
|
|
| ∞
| |
| 5/70
|
| ∞
|
|
| ∞
| ∞
| 4/50
|
| 8/20
|
|
|
| |
| ∞
| 4/50
|
|
|
| ∞
| 5/50
| ∞
|
|
| ∞
| 4/40
|
| |
| 6/40
|
| 5/50
|
|
| ∞
| 5/40
| ∞
| ∞
|
|
|
|
| |
|
|
| 5/50
| ∞
|
|
|
| ∞
| ∞
|
|
| 4/50
|
| |
|
| 4/20
|
| ∞
|
|
| 2/20
| ∞
| ∞
|
|
| 4/30
|
| |
| ∞
| 4/50
|
|
| 5/10
| ∞
| 6/40
|
|
|
| ∞
|
| ∞
| |
|
|
| ∞
|
|
| 2/15
|
| 5/20
|
| 5/30
| ∞
|
|
| |
|
| 4/25
| ∞
|
|
| 5/60
|
| ∞
|
|
| ∞
| 6/15
| ∞
| |
|
| 4/45
|
|
| ∞
| ∞
| 6/20
|
|
| ∞
| 6/40
|
|
| |
|
|
| 4/18
|
| 2/30
| ∞
| ∞
| ∞
|
|
| 4/50
|
|
| |
| 2/60
| 4/10
|
|
| ∞
| ∞
|
|
|
| ∞
|
| 10/15
|
| |
| 4/70
|
| 6/20
| 2/10
|
| ∞
| ∞
| ∞
|
|
|
|
|
| |
| 6/80
| 2/25
|
|
| ∞
| ∞
|
|
|
| ∞
|
|
|
| |
| 2/50
| 2/20
| 2/20
|
|
| ∞
| ∞
| ∞
|
|
|
|
|
| |
| 3/40
|
| ∞
|
|
| ∞
| 12/25
| ∞
|
|
|
| 6/15
| ∞
| |
| ∞
|
| ∞
|
|
| 4/20
| 6/10
| ∞
|
| 8/12
|
|
| ∞
| |
|
|
| ∞
| ∞
|
|
| 10/30
| ∞
| 5/30
|
| 4/30
|
| ∞
| |
|
|
| ∞
|
|
| ∞
| ∞
| 2/20
| 2/20
| 1/20
|
|
|
| |
| 2/12
|
| 4/12
|
| 8/12
| ∞
| ∞
| ∞
|
|
|
|
|
| |
| ∞
|
|
|
|
| ∞
| 2/20
| ∞
|
| 3/30
| ∞
| 4/30
|
| |
| 2/40
|
| ∞
| 4/50
|
|
|
| ∞
| ∞
|
| 2/40
|
| ∞
| |
| 4/50
|
| ∞
|
|
| ∞
| ∞
| 4/50
|
| 3/20
|
|
|
| |
| 2/30
|
| ∞
|
| 8/30
|
| 5/30
| ∞
| ∞
|
|
|
| ∞
|
Расчет электрических цепей переменного тока
Общие положения
Для расчета электрических цепей переменного тока применяются те же методы, что и для цепей постоянного тока, но т.к. переменный синусоидальный ток характеризуется большим количеством параметров и его аналитическое представление сложнее, то это вносит свои особенности в методику расчета.
Наиболее удобной для расчетов является комплексная форма представления синусоидальных функций. На начальном этапе расчета необходимо определить сопротивления всех реактивных элементов (если они не заданы) по формулам (1). В дальнейшем в расчетах использовать их комплексную форму: для активного сопротивления (R), для индуктивного сопротивления (jXL), для емкостного сопротивления (-jXC). Над ЭДС, напряжением, током в комплексной форме ставится точка: 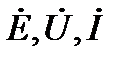 , а под полным сопротивлением и полной проводимостью участка черта снизу: , а под полным сопротивлением и полной проводимостью участка черта снизу:  . .
Основные закономерности, необходимые для расчета эл. цепей переменного тока (комплексная форма)
| закон Ома для участка эл. цепи, с полным комплексным сопротивлением
| 1-ый закон Кирхгофа
| 2-ой закон Кирхгофа
| 
| 
| 
| | Сила тока на участке цепи прямо пропорциональна напряжению участка и обратно пропорциональна его сопротивлению.
| Алгебраическая сумма токов в узле электрической цепи равна нулю.
| Алгебраическая сумма падений напряжения в контуре электрической цепи равна алгебраической сумме ЭДС в нем.
| Далее рассмотрим расчет электрической цепи переменного тока с одним источником методом эквивалентного преобразования схемы. Данный метод содержит общую для всех методик подготовительную часть и в тоже время имеет свою специфику.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 .
. .
Так как в нагрузочной ветви отсутствует источник, то Ен не записываем.
.
Так как в нагрузочной ветви отсутствует источник, то Ен не записываем.
 , откуда
, откуда  . В последнем выражении неизвестна величина I1, которую найдем по 2-му закону Кирхгофа из «контура 2»
. В последнем выражении неизвестна величина I1, которую найдем по 2-му закону Кирхгофа из «контура 2»  , откуда
, откуда .
. .
.

 , А
, А

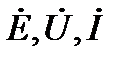 , а под полным сопротивлением и полной проводимостью участка черта снизу:
, а под полным сопротивлением и полной проводимостью участка черта снизу:  .
.

