|
Метод узловых потенциалов
1.3.1 Подписать узлы, расставить произвольно направления токов в ветвях и подписать токи.
1.3.2 Заземлить один любой узел, т.е. принять его потенциал за «0».
1.3.3 Для всех незаземленных узлов составим уравнения по 1-му закону Кирхгофа.
1.3.4 В полученной системе уравнений число искомых токов больше числа уравнений, поэтому выполняем замену переменной, а именно, выражаем искомые токи через потенциалы незаземленных узлов.
*Все токи ветвей представляем выражениями вида 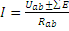 , ,
где Uab – напряжение ветви, между узлами «a» и «b» которой течет ток I, причем ток направлен от узла «a» к узлу «b», в противном случае указываем напряжение Uba;
±∑E – алгебраическая сумма ЭДС ветви ab, в которой ЭДС учитывается со знаком «+», если ток I и ЭДС сонаправлены;
Rab – полное сопротивление ветви ab.
1.3.5 Подставляем выражения п.1.3.4. в уравнения п.1.3.3., подставляем исходные данные, решаем систему и находим потенциалы незаземленных узлов.
1.3.6 Используя выражения п.1.3.4. находим искомые токи ветвей.
1.3.7 Проверяем полученные результаты, например, по балансу мощности.
| Пример расчета методом узловых потенциалов
| | выполняем п. 1.3.1
| выполняем п. 1.3.2
| |
|
φb=0
| | выполняем п. 1.3.3
| | узел «а» -1закон Кирхгофа
| Т.к. незаземлен лишь узел «а», то необходимо составить только одно уравнение
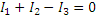
| | выполняем п. 1.3.4
| 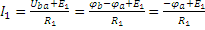 , ,  , ,
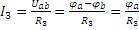 . .
| | выполняем п. 1.3.5
| Подставляем выражения п.1.3.4. в уравнения п.1.3.3., получим:
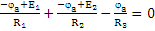 ,
подставляем исходные данные, решаем систему (в рассматриваемом примере система содержит одно уравнение) любым мат. методом и находим потенциалы незаземленных узлов (в данном случае находим ,
подставляем исходные данные, решаем систему (в рассматриваемом примере система содержит одно уравнение) любым мат. методом и находим потенциалы незаземленных узлов (в данном случае находим  ). ).
| | выполняем п. 1.3.6
| | Используя выражения п.1.3.4, после выполнения п.1.3.5, можно найти искомые токи ветвей I1, I2, I3.
| | выполняем п. 1.3.7
| Составим баланс мощностей для схемы п. 1.3.1
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно.
Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно.
|
Метод контурных токов
1.4.1 Подписать узлы, расставить произвольно направления токов в ветвях и подписать токи.
1.4.2 Определить независимые контуры и произвольно выбрать их направления обхода.
1.4.3 Для всех независимых контуров составим уравнения по 2-му закону Кирхгофа.
1.4.4 В полученной системе уравнений число искомых токов больше числа уравнений, поэтому выполняем замену переменной, а именно, выражаем искомые токи ветвей через контурные токи.
*Все токи ветвей представляем выражениями вида
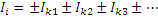 , ,
где 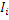 – ток i-ой ветви; – ток i-ой ветви;
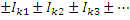 – контурный ток 1-го, 2-го, 3-го и т.д. контуров в которые входит рассматриваемая ветвь. Если ток ветви Ii и контурный ток Ik сонаправлены, то учитывается знак «+». – контурный ток 1-го, 2-го, 3-го и т.д. контуров в которые входит рассматриваемая ветвь. Если ток ветви Ii и контурный ток Ik сонаправлены, то учитывается знак «+».
1.4.5 Подставляем выражения п.1.4.4. в уравнения п.1.4.3., подставляем исходные данные, решаем систему и находим контурные токи.
1.4.6 Используя выражения п.1.4.4. находим искомые токи ветвей.
1.4.7 Проверяем полученные результаты, например, по балансу мощности.
| Пример расчета методом контурных токов
| | выполняем п. 1.4.1
| выполняем п. 1.4.2
| |
|
| | выполняем п. 1.4.3
| Составим уравнения по второму закону Кирхгофа для независимых контуров:
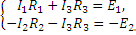
| | выполняем п. 1.4.4
| Укажем контурные токи на схеме и выразим токи ветвей через контурные токи:
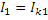 , ,
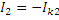 , ,
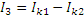 . .
| | выполняем п. 1.4.5
| Подставляем выражения п.1.4.4. в уравнения п.1.4.3., получим:
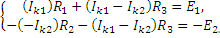 Подставляем исходные данные, решаем систему любым мат. методом и находим контурные токи Ik1, Ik2, Ik3.
Подставляем исходные данные, решаем систему любым мат. методом и находим контурные токи Ik1, Ik2, Ik3.
| | выполняем п. 1.4.6
| | Используя выражения п.1.4.4., можно найти искомые токи ветвей I1, I2, I3.
| | выполняем п. 1.4.7
| Составим баланс мощностей для схемы п. 1.4.1
r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно.
Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно.
|
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


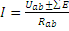 ,
,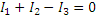
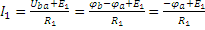 ,
,  ,
,
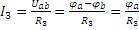 .
.
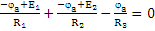 ,
подставляем исходные данные, решаем систему (в рассматриваемом примере система содержит одно уравнение) любым мат. методом и находим потенциалы незаземленных узлов (в данном случае находим
,
подставляем исходные данные, решаем систему (в рассматриваемом примере система содержит одно уравнение) любым мат. методом и находим потенциалы незаземленных узлов (в данном случае находим  ).
).
 Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно.
Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно.
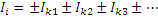 ,
,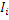 – ток i-ой ветви;
– ток i-ой ветви;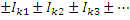 – контурный ток 1-го, 2-го, 3-го и т.д. контуров в которые входит рассматриваемая ветвь. Если ток ветви Ii и контурный ток Ik сонаправлены, то учитывается знак «+».
– контурный ток 1-го, 2-го, 3-го и т.д. контуров в которые входит рассматриваемая ветвь. Если ток ветви Ii и контурный ток Ik сонаправлены, то учитывается знак «+».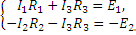
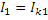 ,
,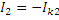 ,
,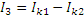 .
.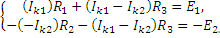 Подставляем исходные данные, решаем систему любым мат. методом и находим контурные токи Ik1, Ik2, Ik3.
Подставляем исходные данные, решаем систему любым мат. методом и находим контурные токи Ik1, Ik2, Ik3.