
|
|
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 1Задача. Найти точки локального экстремума функции и значения функции в них: Решение. а) Находим производную: Решим уравнение Функция f(x) определена и непрерывна на всей числовой оси. Поэтому точка х=11 является критической точкой. Других критических точек нет, так как Исследуем критическую точку, определяя знак первой производной, слева и справа от неё. Таблица 33
Так как на всей числовой оси функция возрастает, то она не имеет экстремумов. б) Находим производную: Решим уравнение Функция f(x) определена и непрерывна на всей числовой оси. Поэтому точки х1=0 и х2=0,25 являются критическими точками. Других критических точек нет, так как f(x) существует всюду. Исследуем критические точки, определяя знак первой производной, слева и справа от каждой точки. Таблица 34
На интервале (0; 0,25) функция возрастает, а на интервалах (-¥; 0) и (0,25; +¥) – убывает. Значит, х1=0 – точка минимума, f(0)=0; х2=0,25 – точка максимума, f(0.25)»0.0596.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 2 Задача. Найти наибольшее и наименьшее значения функции Решение. Найдем критические точки функции f(x), лежащие внутри заданного отрезка: f(-0.9)=9.732; f(-1/3) »12.1296; f(0)=12; f(2.2) »103.476. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции f(x) на отрезке [-0.9; 2.2] равно 103,476 и достигается на правой границе отрезка х=2,2, а её наименьшее значение равно 9,732 и достигается на левой границе отрезка х=-0,9.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 3 Задача. Найти точки перегиба, промежутки выпуклости и вогнутости функции Решение. Найдем последовательно первую и вторую производную функции f(x): Решим уравнение Определим знак второй производной слева и справа от точки Таблица 35
Значит, на интервале (-¥; -4/9) график функции выпуклый, на интервале (-4/9; +¥) график функции вогнутый, х=-4/9 – точка перегиба.
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 4 Задача. Найти градиент функции в точке М(1; -3) и найти производную в той же точке по направлению MN, если N(0; -5). Решение. а) Находим частные производные: б) Найдем единичный вектор l, имеющий данное направление: откуда Вычислим частные производные функции в точке М(1; -3): Получаем,
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 5 Задача. Исследовать функцию Решение. Найдем частные производные функции z и приравняем их к нулю: Её решением являются пары (0; 0) и Вычислим D в точках М0 и М1: Так как в точке М1 РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 2 Задача 1. Методом Пауэлла найти точку минимума х* функции f(x) с точностью e и минимум f*. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. Задача 2. В предыдущей задаче выделить интервал, содержащий минимум функции, так, чтобы концы интервала были целыми числами, и найти минимум той же функции с заданной точностью методом золотого сечения.
Задача 3. Минимизировать функцию методом наискорейшего спуска, заканчивая вычисления при 1. 2. 3. 4. 5. 6. 7. 8. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
Задача 4. Найти глобальное решение задачи методом Лагранжа: Таблица 36
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАЧИ 1 Задача. Найти минимальное значение f* и точку минимума х* функции Решение. Пусть начальная точка x1 =1 и длина шага Dx = 1. Для проверки на окончание поиска используем условие: Итерация 1. Шаг 1. Шаг 2. Шаг 3. Шаг 4.
Шаг 5. Используя метод параболической аппроксимации, находим
Шаг 6. Проверка на окончание поиска: Продолжаем поиск.
Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке Итерация 2. Шаг 4. Шаг 5. Шаг 6. Проверка на окончание поиска: Условия окончания поиска выполняются, следовательно, вычисления заканчиваем. Получили

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
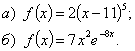

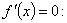
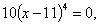 х=11.
х=11.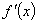 существует всюду.
существует всюду.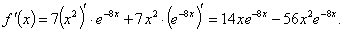
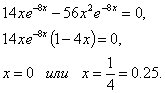
 на интервале [-0.9; 2.2].
на интервале [-0.9; 2.2].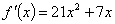 ,
, 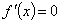 при х1=0 и х2=-1/3. Эти точки лежат внутри рассматриваемого отрезка и являются критическими. Вычислим значения функции на концах отрезка и в критических точках:
при х1=0 и х2=-1/3. Эти точки лежат внутри рассматриваемого отрезка и являются критическими. Вычислим значения функции на концах отрезка и в критических точках:
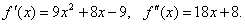

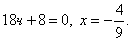

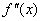
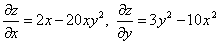 и их значения в точке М(1; -3):
и их значения в точке М(1; -3):

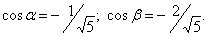
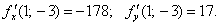

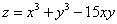 на локальный экстремум.
на локальный экстремум.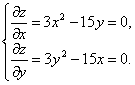
 , т.е. на экстремум надо проверить точки М0(0; 0) и М1
, т.е. на экстремум надо проверить точки М0(0; 0) и М1 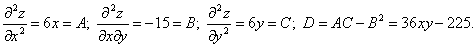
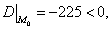 значит экстремума в точке М0 нет;
значит экстремума в точке М0 нет;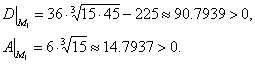
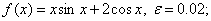
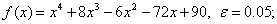
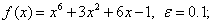
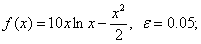
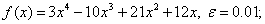
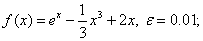
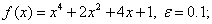

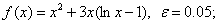
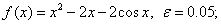
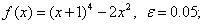
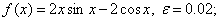

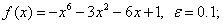
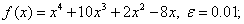
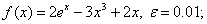
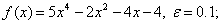
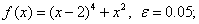
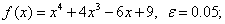


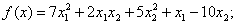
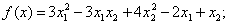


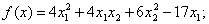
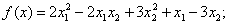

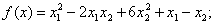
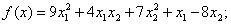
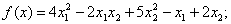
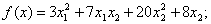

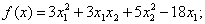




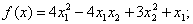


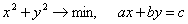
 методом Пауэлла. Точку х* найти с точностью e=0,1.
методом Пауэлла. Точку х* найти с точностью e=0,1.
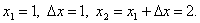
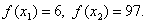
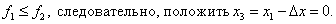
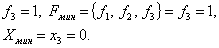

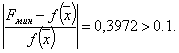
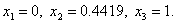 Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.


