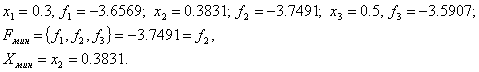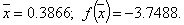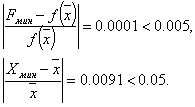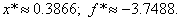|
|
Метод параболической аппроксимации
Метод заключается в замене нелинейной функции f(x) квадратичной параболой f2(x), построенной по трем точкам, принадлежащим f(x), с последующим нахождением максимума (минимума) параболической функции, используя аналитические условия оптимальности: На первом этапе в качестве исходных трех точек используется В этих точках вычисляется f(x) и по полученным точкам f(x1), f(x2), f(x3) строится парабола коэффициенты которой находятся из решения соответствующей системы уравнений: Условие оптимальности приводит к уравнению где х4 – точка максимума (минимума) параболы f2(x). Далее выбирается новый отрезок, внутри которого находится точка х4, и, используя х3, х4, строится новая парабола, по которой уточняется положение максимума (минимума) f(x) и т. д. До тех пор, пока величина отрезка, внутри которого находится оптимум, не будет меньше заданной погрешности e. Таким образом, метод имеет итерационный характер. К достоинству метода относится высокая скорость сходимости, хотя метод может не всегда сходится. На рис. 19 рассмотрена ситуация, когда метод параболической аппроксимации сходится к решению уже на третьем этапе. Парабола, построенная по точкам х3, х4, х5, практически совпадает с исходной функцией. На рис. 20 парабола не имеет максимума уже на втором этапе. В первом случае решение найти можно, во втором – нельзя.
Пример 19. Дана функция f(x) = sin (x + 1). Найти максимум на интервале [-1; 2], точность e = 0,01. Решение. Для построения аппроксимирующей параболы находим точки Решение системы можно найти любым из известных способов, например, по формулам Крамера. На первом шаге получаем Таблица 14
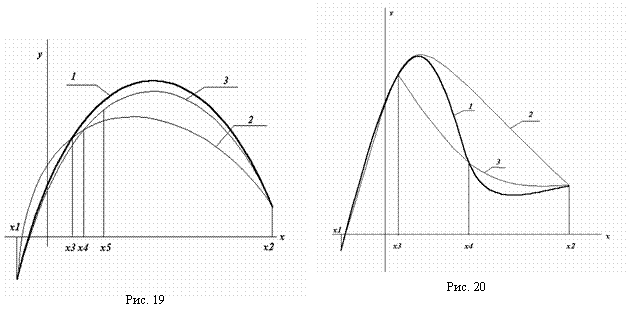
Поскольку уже на третьем шаге разница между двумя точками максимума менее заданной погрешности, то поиск можно заканчивать (четвертый шаг присутствует для наглядности вычислений). Поэтому х* »0,5708, и f* » f (0,5708) = 1. Для реализации данного метода существует ещё один подход. Если задана последовательность точек х1, х2, х3 и известны соответствующие этим точкам значения функции f1, f2, f3, то можно определить постоянные величины а0, а1, а2 таким образом, что значения квадратичной функции совпадут со значениями f(x) в трех указанных точках. Перейдем к вычислению q(x) в каждой из трех заданных точек. Прежде всего, так как Поскольку Наконец, при х = х3 Разрешая последнее уравнение относительно а2, получаем Таким образом, по трем заданным точкам и соответствующим значениям функции можно оценить параметры аппроксимирующего квадратичного полинома достаточно высоко, значит, в соответствии с предложенной стратегией поиска построенный полином можно использовать для оценивания координаты точки оптимума. Напомним, что стационарные точки функции одной переменной определяются путем приравнивания к нулю ее первой производной и последующего нахождения корней полученного таким образом уравнения. В данном случае из уравнения можно получить Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина Видно, что оба подхода отличаются друг от друга только способом вычисления коэффициентов (в первом случае - C0, C1, C2; во втором - а0, а1, а2) квадратичного полинома. Результаты при этом нисколько ни отличаются. Легко убедиться, что для практических вычислений удобнее использовать формулы Пример 20. Найти минимальное значение f* и точку минимума х* функции Решение. Значения х1, х2, х3 находим также как и в предыдущем примере. Таблица 15
Уже после второго шага можно закончить вычисления, так как заданная точность достигнута (1,7317-1,7236 = 0,0081 < e = 0,05). Значит, х* »1,7317, и f* » f (1,7317) = -92,1384. Пример 21. Найти точку минимума х* функции Решение. Вычисления представим в виде табл. 16: Таблица 16
Точность достигнута (0,3934 – 0,352 = 0,414 < e = 0,05). Значит, х* »0,352, и f* » f (0,352) = -3,7373.
Метод Пауэлла
Этот метод, разработанный Пауэллом, основан на последовательном применении процедуры оценивания с использованием квадратичной аппроксимации. Схему алгоритма можно описать следующим образом. Пусть х1 – начальная точка, Dх – выбранная величина шага по оси х. Алгоритм метода Пауэлла: Шаг 1. Вычислить Шаг 2. Вычислить f(x1) и f(x2). Шаг 3. Если f(x1) > f(x2), положить Шаг 4. Вычислить f(x3) и найти Шаг 5. По трем точкам х1, х2, х3 вычислить Шаг 6. Проверка на окончание поиска. а) является ли разность б) является ли разность Если оба условия выполняются, закончить поиск. В противном случае перейти к шагу 7. Шаг 7. Выбрать «наилучшую» точку ( Заметим, что при первой реализации шага 5 границы интервала, содержащего точку минимума, не обязательно оказываются установленными. При этом полученная точка Пример 22. Минимизировать функцию f(x) = 2x2 + (16/x). Решение. Пусть начальная точка x1 = 1 и длина шага Dx = 1. Для проверки на окончание поиска используются следующие параметры сходимости: Итерация 1. Шаг 1. Шаг 2. Шаг 3. Шаг 4. Шаг 5. Используя метод параболической аппроксимации, находим Шаг 6. Проверка на окончание поиска: Следовательно, продолжаем поиск. Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке Итерация 2. Шаг 4. Шаг 5. Шаг 6. Проверка на окончание поиска: Следовательно, продолжаем поиск. Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке Итерация 3. Шаг 4. Шаг 5. Шаг 6. Проверка на окончание поиска: Точность достигнута. Следовательно, поиск закончен. Получили Пример 23. Найти минимальное значение f* и точку минимума х* функции Решение. Пусть начальная точка x1 =3 и длина шага Dx = 1. Для проверки на окончание поиска используются следующие параметры сходимости: Итерация 1. Шаг 1. Шаг 2. Шаг 3. Шаг 4. Шаг 5. Используя метод параболической аппроксимации, находим Шаг 6. Проверка на окончание поиска: Так как пункт а) не выполняется, то продолжаем поиск. Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке Итерация 2. Шаг 4. Шаг 5. Шаг 6. Проверка на окончание поиска: Следовательно, продолжаем поиск. Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке
Итерация 3. Шаг 4. Шаг 5. Шаг 6. Проверка на окончание поиска: Продолжаем поиск. Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке Итерация 4. Шаг 4. Шаг 5. Шаг 6. Проверка на окончание поиска: Условия окончания поиска выполняются, следовательно, вычисления заканчиваем. Получили Пример 24. Найти точку минимума х* функции Решение. Пусть начальная точка x1 = 0,5 и длина шага Dx = 0,2. Для проверки на окончание поиска используются следующие параметры сходимости: Итерация 1. Шаг 1. Шаг 2. Шаг 3. Шаг 4. Шаг 5. Используя метод параболической аппроксимации, находим Шаг 6. Проверка на окончание поиска: Так как пункт а) не выполняется, то продолжаем поиск. Шаг 7. Выбираем «наилучшую» точку, и точки, их окружающие. Обозначаем эти точки в естественном порядке Итерация 2. Шаг 4.
Шаг 5. Шаг 6. Проверка на окончание поиска: Условия окончания поиска выполняются, следовательно, вычисления заканчиваем. Получили

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


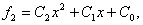
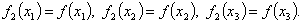


 = 0,5571, f(
= 0,5571, f( 

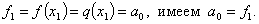

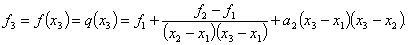
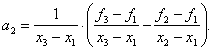
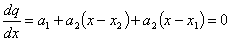
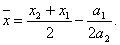

 на отрезке [1.5; 2]. Точку х* найти с точностью e=0,05.
на отрезке [1.5; 2]. Точку х* найти с точностью e=0,05. на отрезке [0.5; 1] с точностью e=0,05.
на отрезке [0.5; 1] с точностью e=0,05.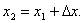
 Если
Если  положить
положить 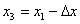 .
.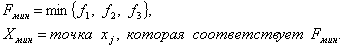

 достаточно малой?
достаточно малой? достаточно малой?
достаточно малой? ) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.
) и две точки по обе стороны от нее. Обозначить эти точки в естественном порядке и перейти к шагу 4.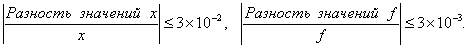

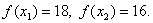
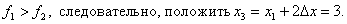



 Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.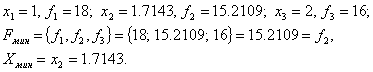
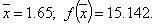
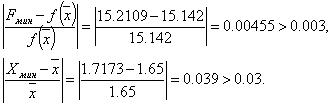
 Переходим к итерации 3, которая начинается с шага 4.
Переходим к итерации 3, которая начинается с шага 4.

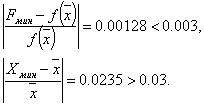






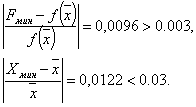
 Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.

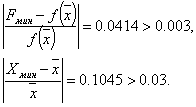
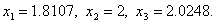 Переходим к итерации 3, которая начинается с шага 4.
Переходим к итерации 3, которая начинается с шага 4.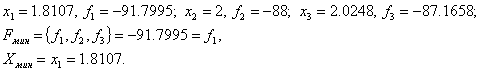
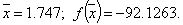

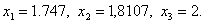 Переходим к итерации 4, которая начинается с шага 4.
Переходим к итерации 4, которая начинается с шага 4.


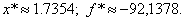

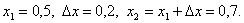



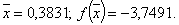
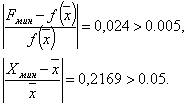
 Переходим к итерации 2, которая начинается с шага 4.
Переходим к итерации 2, которая начинается с шага 4.