|
|
Свойства и характеристики нечётких множествЛАБОРАТОРНАЯ РАБОТА №1 СОЗДАНИЕ НЕЧЕТКОГО МНОЖЕСТВА И ЕГО ГРАФИЧЕСКОЕ
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Введение. Основы нечеткой логики были заложены в конце 60-х лет в работах известного американского математика Латфи Заде. Исследования такого рода было вызвано возрастающим неудовольствием экспертными системами. Хваленый "искусственный интеллект", который легко справлялся с задачами управления сложными техническими комплексами, был беспомощным при простейших высказываниях повседневной жизни, типа "Если в машине перед тобой сидит неопытный водитель - держись от нее подальше". Для создания действительно интеллектуальных систем, способных адекватно взаимодействовать с человеком, был необходим новый математический аппарат, который переводит неоднозначные жизненные утверждения в язык четких и формальных математических формул. Первым серьезным шагом в этом направлении стала теория нечетких множеств, разработанная Заде. Его работа "Fuzzy Sets", опубликованная в 1965 году в журнале "Information and Control", заложила основы моделирования интеллектуальной деятельности человека и стала начальным толчком к развитию новой математической теории. Он же дал и название для новой области науки - "fuzzy logic" (fuzzy - нечеткий, размытый, мягкий). Аппарат теории нечетких множеств, продемонстрировав ряд многообещающих возможностей применения - от систем управления летательными аппаратами до прогнозирования итогов выборов, оказался вместе с тем сложным для воплощения. Учитывая имеющийся уровень технологии, нечеткая логика заняла свое место среди других специальных научных дисциплин - где-то посредине между экспертными системами и нейронными сетями.
Определение множества. Пусть Е – множество, а А – подмножество Е:
Если элемент х является элементом подмножества А, то это обозначают как:
Также, для выражения такой принадлежности можно использовать характеристическую функцию µА (х), значения которой показывают, является ли х элементом А:
Пример. Рассмотрим конечное множество из пяти элементов Е: Е = {x1, x2, x3, x4, x5}, (4) и пусть А = { x2, x3, x5} (5) Получим для каждого элемента из множества Е его степень принадлежности множеству А: µА (х1) = 0, µА (х2) = 1, µА (х3) = 1, µА (х4) = 0, µА (х5) = 1. Это позволяет представить А через все элементы множества Е, сопроводив каждый из них значением его функции принадлежности: А = {(x1, 0),(x2, 1), (x3,1), (x4,0), (x5, 1)} (6)
Нечеткое множество (НМ). Нечеткое множество отличается от обычного тем, что для всех или части его элементов не существует однозначного ответа на вопрос, принадлежит или не принадлежит элемент данному нечеткому множеству [1]. Степень принадлежности выражается числом от 1 до 0. Нечеткое множество использует понятие универсального множества или универсума. Универсальное множество (универсум) – множество, содержащее все мыслимые объекты. Под нечётким множеством
где
Функция
Рисунок 1 – Нечёткое множество и классическое, четкое множество Свойства и характеристики нечётких множеств · Множество α-уровня – это обычное множество, удовлетворяющее след. условию:
Например, для α=0.2 х={0,0,0,1,1}для примера с оценками [2]. · Величина · Нечеткое множество A является нормальным, если его высота равняется 1, то есть верхняя граница ее функции принадлежности = 1 ( · При · Ближайшее четкое множество к данному НМ – характеристическая функция такого множества описывается след. выражением:
· Нечеткое множество является пустым, если
· Нечеткое множество является унимодальным, если · Ядро НМ – такое НМ, элементы которого удовлетворяют условию · Элементы x ϵ E, для которых · Носителем (суппортом) нечёткого множества Виды функций принадлежности НМ: ·
(11)
· Трапециевидные:
(12)
rде а, b, с, d - некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением: а< b< с< d. · Z-образная функция (характеризуются НМ типа «малое кол-во», «небольшое значение», «незначительная величина»):
(13)
· S-образная функция (характеризуются НМ типа «большое кол-во», «большое значение», «большая величина»):
(14)
· П- образная функция принадлежности напоминает по внешней форме колокол:
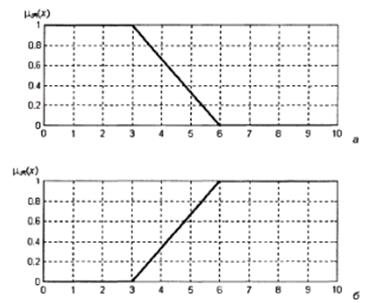
В аппарате нечетких множеств существует определенный набор стандартных функций принадлежности. Например, в [3, 4], а также в справочной системе пакета Matlab можно встретить такие ФП: 1. trimf – классическая треугольная функция принадлежности. 2. trapmf – трапецеидальная функция принадлежности. 3. sigmf – сигмоидальная функция принадлежности 4. dsigmf – определяется как разность двух сигмоидальных функций 5. gbellmf – функция принадлежности так называемого обобщенного колоколообразного типа: 6. 7. gaussmf – Гауссова функция принадлежности, определяется как 8. gauss2mf – разность двух гауссовых функций принадлежности 9. smf – т.н. s-образная функция принадлежности. Задана кусочно: 10. 11. zmf – z-образная функция принадлежности, задана кусочно: 12. pimf – p-образная функция принадлежности: 13. 14. psigmf – произведение двух сигмоидальных функций 15. Методы построения функций принадлежности. Выделяют две группы методов построения по экспертным оценкам функций принадлежности нечеткого множества Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. К группе данных методов можно отнести такие методики построения функций принадлежности, как построение функций принадлежности на основе парных сравнений, с использованием статистических данных, на основе ранговых оценок и т.д. ХОД РАБОТЫ Данная работа является базовой для выполнения остальных работ 1.Создать класс «универсальное множество». Оно может быть как дискретным, так и непрерывным. Ориентировочная структура класса предлагается такая: · Флаг «дискретное/непрерывное универсальное множество». · Массив значений универсального множества. Создается динамически, количество элементов задается в программе. В случае, если флаг выставлен в «дискретное множество», массив является строковым, представляет собой перечень элементов множества. В случае, если флаг выставлен в значение «непрерывное множество», массив имеет вещественный тип. Например, процесс заполнения экземпляра класса может быть таким: · Задать флаг дискретные/непрерывные значения элементов универсального множества. · Указать число элементов в массиве, создать динамический массив. В случае дискретных значений элементов универсального множества создавать массив строк, в случае непрерывных – создать массив вещественных чисел. Возможно предусмотреть несколько конструкторов для этой цели. · В случае дискретных значений элементов универсального множества заполнить массив вручную, с клавиатуры. · В случае непрерывных – возможно просто ввести минимум и максимум разрешенного интервала для универсального множества, заполнить массив автоматически для уже заданного числа точек в интервале, создавая точки (значения универсального множества) через равные промежутки разрешенного интервала. 2.Создать класс «нечеткое множество». Класс должен содержать значения функции принадлежности (множества назначений) для уже заданного ранее универсального множества. Класс может иметь такие элементы: · Ссылка на константу типа «универсальное множество», которая содержит значения универсального множества для данного нечеткого множества. · Массив из элементов – значений функции принадлежности. Размерность массива должна соответствовать размерности массива значений переменной, содержащей универсальное множество. · Ориентировочный предлагаемый процесс заполнения значений переменной класса «нечеткое множество» предлагается такой: · Создать переменную класса «нечеткое множество» · Динамически создать массив «значения функции принадлежности». Размерность массива берется равной размерности массива в классе «универсальное множество», тип массива – вещественный, массив может содержать значения от 0 до 1 (разрешенный интервал для множества назначений). · Выбрать тип функции принадлежности, например, с помощью компонента «ListBox». Например, компонент может принимать значения «Z – Z-образная функция принадлежности, S – S-образная, П – П-образная, A(arbitrary - произвольная)». · В случае, если выбрана произвольная форма функции принадлежности нечеткой переменной, произвести ввод вручную значений массива. · В случае, если выбрана S или Z – образная функция принадлежности, необходимо задать ее двумя числами – абсциссами верхней и нижней точек (см. рис 1 а, б).
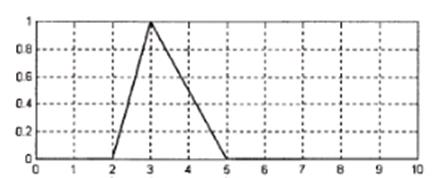
Рис.1. Ориентировочный вид Z (а) и S (б) – образных функций принадлежности. Далее массив переменной «функция принадлежности» задается с помощью нахождения ординат по введенной функции для уже заданного массива абсцисс (в переменной «универсальное множество»). · В случае, если выбрана П – образная функция принадлежности, необходимо задать ее с помощью трех точек – абсцисс левого и правого краев, а также центра (рис.2). Далее процесс заполнения массива переменной функции принадлежности не отличается от описанного в предыдущем пункте.
Рис. 2. Ориентировочный вид П-образной функции принадлежности. 3.Реализовать возможность ее графического отображения. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТОВ ПО ЛАБОРАТОРНЫМ РАБОТАМ 1. Отчеты по лабораторным работам должны включать: - титульный лист с указанием № работы, названия дисциплины, темы, группы, ФИО студента на украинском языке; - № варианта и условие задания; - листинги всех программных файлов проекта. 2. При сдаче отчета обязательна загрузка проекта и демонстрация работы программы.
ЛИТЕРАТУРА 1. Леоненков А.В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. – СПб., 2003. 2. Кофман А. Введение в теорию нечетких множеств. М.: Радио и связь, 1982. 3. Дьяконов В. Математические пакеты MATLAB. Специальный справочник / Дьяконов В., Круглов В. – СПб.: Питер, 2001. – 480с.: ил. 4. Алтунин А.Е. Модели и алгоритмы принятия решений в нечетких условиях: Монография./ Алтунин А.Е., Семухин М.В. - Тюмень: Издательство Тюменского государственного университета, 2000. - 352 с.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
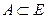 (1)
(1)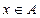 (2)
(2)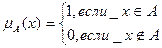 (3)
(3)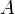 понимается совокупность
понимается совокупность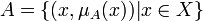 (7)
(7)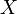 – универсальное множество,
– универсальное множество,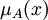 – функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента
– функция принадлежности (характеристическая функция), характеризующая степень принадлежности элемента  нечёткому множеству
нечёткому множеству 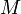 называют множеством принадлежностей, часто в качестве M выбирается отрезок [0, 1]. Значение 0 означает, что элемент не включен в нечёткое множество, 1 – описывает полностью включенный элемент. Значения между 0 и 1 характеризуют нечётко включенные элементы. Если M={0,1}, то нечёткое множество может рассматриваться как обычное, чёткое множество.
называют множеством принадлежностей, часто в качестве M выбирается отрезок [0, 1]. Значение 0 означает, что элемент не включен в нечёткое множество, 1 – описывает полностью включенный элемент. Значения между 0 и 1 характеризуют нечётко включенные элементы. Если M={0,1}, то нечёткое множество может рассматриваться как обычное, чёткое множество.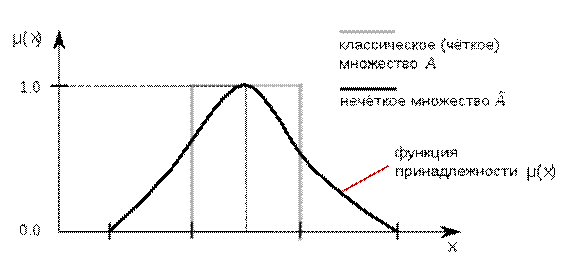
 (8)
(8)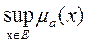 называется высотой нечеткого множества A. Это максимальное значение функции принадлежности элементов нечеткого множества.
называется высотой нечеткого множества A. Это максимальное значение функции принадлежности элементов нечеткого множества.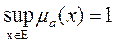 ).
).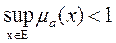 нечеткое множество называется субнормальным.
нечеткое множество называется субнормальным. (9)
(9) . Непустое субнормальное нечёткое множество можно нормализовать по формуле:
. Непустое субнормальное нечёткое множество можно нормализовать по формуле: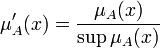 (10)
(10)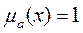 лишь для одного x из E.
лишь для одного x из E.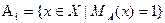 , т.е. все элементы функции принадлежности = 1.
, т.е. все элементы функции принадлежности = 1. называются точками перехода множества A.
называются точками перехода множества A.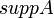 называется множество
называется множество 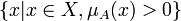 .
.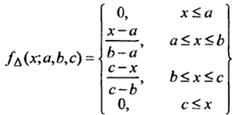 Треугольные:
Треугольные: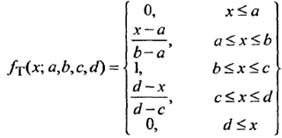
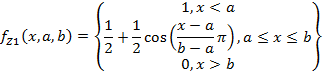

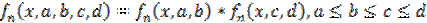 (15)
(15)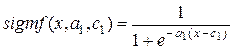 (16)
(16) . (17)
. (17)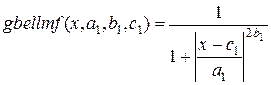 (18)
(18) (19)
(19) (20)
(20) (21)
(21) (22)
(22)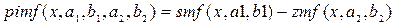 . (23)
. (23)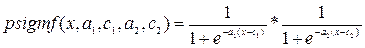 (24)
(24)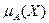 : прямые и косвенные методы.
: прямые и косвенные методы.