
|
|
Структура, основные элементы и операции в нечетких моделяхРассмотрим типовую структуру нечеткой модели системы с двумя входами и одним выходом.
Рисунок 1.5 – Структура нечеткой модели системы с двумя входами и одним выходом Типовая структура нечеткой модели системы состоит из 3-х блоков. 1. Блок Фаззификация (Fuzzification) вычисляет степени принадлежности входных четких числовых значений
Рисунок 1.6 – Примеры функций принадлежности нечетких множеств с указанием их области определения Вычисленные и представленные на выходе блока фаззификации степени принадлежности 2. Блок Вывод (Inference) на входе получает степени принадлежности 1) база правил; 2) механизм вывода; 3) функции принадлежности выходного параметра База правил содержит логические правила, которые задают имеющие место в системе причинно-следственные отношения между нечеткими значениями ее входных и выходных величин. Пример. База правил имеет вид: R1: если ( R2: если ( R3: если ( R4: если ( где нечеткие значения входных параметров (
Рисунок 1.7 – Примеры функций принадлежности нечетких значений вывода модели с указанием области определения Решение возложенной на блок вывода задачи, связанной с определением результирующей функции принадлежности IM1: элемент, вычисляющий степень выполнения каждого правила IM2: элемент, вычисляющий активационные функции принадлежности заключений каждого правила IM3: элемент, вычисляющий результирующую функцию принадлежности Пример. Механизм вывода для системы с двумя входами. IM1: агрегация условий правил с использованием оператора PROD для пересечения множеств (И) и оператора MAX для объединения множеств (ИЛИ); IM2: определение активизированных функций принадлежности заключений правил с использованием оператора импликации Мамдани; IM3: определение результирующей функции принадлежности 3. Блок Дефаззификация (Defuzzification) на основе результирующей функции принадлежности Фаззификация В блоке фаззификации вычисляются степени принадлежности числовых значений входных параметров модели входным нечетким множествам.
Рисунок 1.8 – Блок фаззификации и пример его работы В примере (см. рисунок 1.8) равенство 0,3 степени принадлежности входного значения Для вычисления степеней принадлежности значений конкретным нечетким множествам, функции принадлежности последних должны быть точно заданы на качественном (вид функции) и количественном (ее параметры) уровне. Как форма функции принадлежности, так и ее параметры, оказывают существенное влияние на точность модели. Пример математического описания функций принадлежности.
Вывод Блок вывода на основе степеней принадлежности
Рисунок 1.9 – Блок вывода нечеткой модели Операция вывода включает в себя следующие шаги: 1) вычисление степеней выполнения отдельных правил (т.е. их условий); 2) определение активационных функций принадлежности заключений отдельных правил; 3) определение результирующей функции принадлежности вывода из всех правил, входящих в базу. В классической логике разработан ряд правил рассуждений (такие рассуждения называются тавтологиями). Тавтология – это тождественно-истинная формула в исчислении высказываний, которая при любых возможных истинностных значений входящих в нее переменных истинна. Одним из правил является Modus Ponens, по которому процесс рассуждений имеет вид:
В классической тавтологии типа Modus Ponens для условия ( ЕСЛИ ( Лишь в этом случае импликацию можно использовать в процессе рассуждений. Как условная, так и заключительная части правил должны иметь строгую, детерминированную формулировку. Утверждения, содержащие неточные, размытые формулировки, например, ( ( ( являются недопустимыми. В нечетком моделировании и управлении применяются приближенные рассуждения, позволяющие использовать в условиях и заключениях правил нечеткие формулировки. Приближенное рассуждение, основанное на тавтологии типа Обобщенный (generalized) Modus Ponens (GMP), имеет вид:
Здесь
Пример рассуждения на основе GMP:
Рассуждения, основанные на Modus Ponens, не всегда дают хорошие результаты. Пример:
В примере приближенное рассуждение, основанное на GMP, приводит к заключению «кожа становится очень загорелой». В реальности после чересчур длительного пребывания на солнце кожа становится красной из-за солнечного ожога. Правило вывода GMP можно использовать в том случае, если оно допускает возможность экстраполяции, которая позволяет его применять и тогда, когда 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ,
,  входным нечетким множествам
входным нечетким множествам  ,
,  . Для выполнения указанной операции блок фаззификации должен иметь доступ к точно определенным функциям принадлежности
. Для выполнения указанной операции блок фаззификации должен иметь доступ к точно определенным функциям принадлежности  ,
,  входов.
входов.
 ,
,  ) или большими (
) или большими (  ,
, 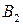 ).
). .
. ) И (
) И (  ) ТО (
) ТО (  ),
), ) ТО (
) ТО (  ),
),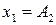 ) И (
) И (  ), (1.10)
), (1.10)
 , обеспечивается механизмом вывода. Он состоит из следующих элементов:
, обеспечивается механизмом вывода. Он состоит из следующих элементов: в отдельности;
в отдельности;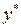 выходного параметра, являющееся результатом для входных числовых значений
выходного параметра, являющееся результатом для входных числовых значений 
 нечеткому множеству
нечеткому множеству  ,
, 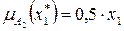 ,
, ,
,  .
. ,
,  входных значений определяет результирующую функцию принадлежности (рисунок 1.9).
входных значений определяет результирующую функцию принадлежности (рисунок 1.9).

 ) и заключения (
) и заключения ( 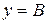 ) допустимы только два дискретных значения истинности – 0 и 1, а факт (
) допустимы только два дискретных значения истинности – 0 и 1, а факт ( 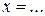 ) должен полностью соответствовать условной части импликации:
) должен полностью соответствовать условной части импликации: ),
), ),
), ),
),
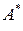 и
и  могут, например, иметь вид:
могут, например, иметь вид: ,
, и т.п.
и т.п.

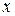 лишь приблизительно равно
лишь приблизительно равно 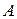 (нет точной согласованности факта с условием правила). Получаемые заключения (y приблизительно равно B) также «приближенно» согласуются с действительностью.
(нет точной согласованности факта с условием правила). Получаемые заключения (y приблизительно равно B) также «приближенно» согласуются с действительностью.