Нечеткие отношения и операции над ними
Опр. 1. Отношением  на множестве на множестве  называется некоторое подмножество декартова произведения называется некоторое подмножество декартова произведения  . .
В соответствии с этим определением задать отношение  на множестве на множестве  означает указать все пары означает указать все пары  , которые связаны отношением , которые связаны отношением  . Для обозначения того, что элементы . Для обозначения того, что элементы  связаны отношением, будем пользоваться следующими двумя эквивалентными формами записи: связаны отношением, будем пользоваться следующими двумя эквивалентными формами записи:  или или  . .
Если множество  , на котором задано отношение , на котором задано отношение  , конечно, то отношение задается в двух формах: , конечно, то отношение задается в двух формах:
1) в матричной:
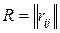 , ,  , ,  , ,
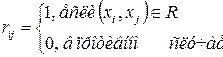
2) в графовой:
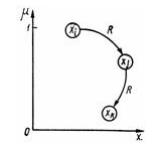
Пусть на множестве  заданы два отношения заданы два отношения 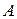 и и  , множество , множество 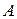 определяется матрицей определяется матрицей  , ,  - матрицей - матрицей 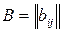 . .
Тогда рассмотрим отношение  , которое является объединением двух отношений: , которое является объединением двух отношений:  . .
Если 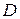 является пересечением отношений является пересечением отношений 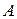 и и  , то , то 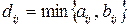 . .
Опр. 2. Отношение  включает в себя отношение включает в себя отношение 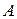 , если для соответствующих множеств , если для соответствующих множеств  и и  выполняется условие выполняется условие  . .
Опр. 3. Если между 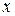 и и  существует отношение существует отношение  , то обратным к нему называется такое отношение , то обратным к нему называется такое отношение 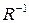 , что , что 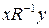 существует тогда и только тогда, когда существует тогда и только тогда, когда  . Если при этом . Если при этом  , , 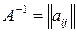 - матрицы этих отношений, то элементы этих матриц связаны соотношением: - матрицы этих отношений, то элементы этих матриц связаны соотношением:  , ,  . .
Опр. 4. Произведение (композиция) отношений 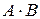 на декартовом произведении на декартовом произведении  определяется следующим образом: определяется следующим образом:  тогда и только тогда, когда существует такой тогда и только тогда, когда существует такой 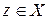 , для которого выполнены одновременно отношения , для которого выполнены одновременно отношения  и и  . При этом элементы матриц отношений связаны следующим образом: . При этом элементы матриц отношений связаны следующим образом:
 . .
Основные свойства отношений:
1. Отношение  рефлексивно, если рефлексивно, если 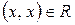 или или  для любого для любого  . .
Пример рефлексивного отношения на множестве действительных чисел: отношение  (‘больше-равно’). (‘больше-равно’).
2. Отношение  на на  антирефлексивно, если из того, что антирефлексивно, если из того, что  следует следует  . В матрице рефлексивного отношения все диагональные элементы равны 1, а антирефлексивного – 0. . В матрице рефлексивного отношения все диагональные элементы равны 1, а антирефлексивного – 0.
3. Отношение  симметрично, если из того, что симметрично, если из того, что  следует следует  . Матрица симметричного отношения – симметричная. Отношение называется антисимметричным, если из того, что . Матрица симметричного отношения – симметричная. Отношение называется антисимметричным, если из того, что  и и  , следует , следует 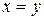 . .
4. Для транзитивного отношения выполняется следующее условие:  . .
Нечеткие отношения
Опр. 5. Нечетким отношением  на универсальном множестве на универсальном множестве  называется нечеткое подмножество декартова произведения называется нечеткое подмножество декартова произведения  , которое характеризуется такой функцией принадлежности , которое характеризуется такой функцией принадлежности  , что , что  . Причем . Причем  принимается как субъективная мера выполнения отношения принимается как субъективная мера выполнения отношения  . .
Или другой способ записи:
 . .
В общем случае  -арное отношение есть нечеткое подмножество -арное отношение есть нечеткое подмножество  декартового произведения универсальных множеств декартового произведения универсальных множеств 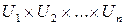 , причем: , причем:
 . .
Пример 1. Пусть заданы:
а) четкое отношение   , где , где  ; ;
б) нечеткое отношение  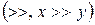 . .
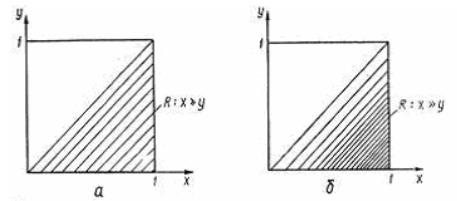
Рисунок 1.3 – Примеры задания отношений   и и  
На рисунке 1.3 приведены пары  из интервала из интервала 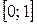 , связанные отношением , связанные отношением  , то есть такие, что , то есть такие, что  . Они образуют множество точек заштрихованной области, которые отделены четкой границей – диагональю от других точек. . Они образуют множество точек заштрихованной области, которые отделены четкой границей – диагональю от других точек.
Строя нечеткое отношение 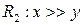 на единичном квадрате, убеждаемся, что существуют пары на единичном квадрате, убеждаемся, что существуют пары  , которые можно определенно отнести ко множеству , которые можно определенно отнести ко множеству  (например, точка (например, точка  ), а также те, которые определенно не принадлежат ), а также те, которые определенно не принадлежат  (например, (например,  ). ).
Кроме того, имеется нечеткое множество пар  , о принадлежности которых к множеству , о принадлежности которых к множеству  можно судить лишь приблизительно с определенной субъективностью (например, точка можно судить лишь приблизительно с определенной субъективностью (например, точка  ). Поэтому нечеткое множество ). Поэтому нечеткое множество  характеризуется отсутствием четкой границы от дополнительного множества характеризуется отсутствием четкой границы от дополнительного множества  , и степень принадлежности , и степень принадлежности  пары пары  следует характеризовать плотностью штриховки (рисунок 1.3,б). Можно рассмотреть некоторые сечения отношения следует характеризовать плотностью штриховки (рисунок 1.3,б). Можно рассмотреть некоторые сечения отношения  при фиксированном при фиксированном  . .
Соответствие семейство функций  приведено на рисунке 1.4. Если нечеткое отношение приведено на рисунке 1.4. Если нечеткое отношение  на на  конечно, то его функция принадлежности конечно, то его функция принадлежности  задается в виде квадратной матрицы задается в виде квадратной матрицы  , ,  , , 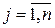 с элементами с элементами  . Если . Если  , то это означает, что степень выполнения отношения , то это означает, что степень выполнения отношения 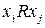 равна равна  . .
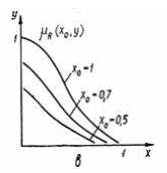
Рисунок 1.4 – Некоторые сечения отношения 
Пример 2. Пусть  . Отношение . Отношение  можно задать функцией принадлежности можно задать функцией принадлежности
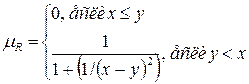
Пример 3. Пусть  , ,  , , 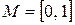 . Нечеткое отношение . Нечеткое отношение  может быть задано, к примеру, в виде таблицы: может быть задано, к примеру, в виде таблицы:
Пример 4. Нечеткое отношение  , для которого , для которого  , при достаточно больших , при достаточно больших  можно интерпретировать так: « можно интерпретировать так: « 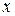 и и  близкие друг к другу числа» близкие друг к другу числа»
Опр. 5. Носителем нечеткого отношения  на множестве на множестве  называется подмножество декартова произведения называется подмножество декартова произведения  , определяемое как: , определяемое как:
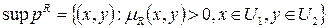
Пример 5. Пусть нечеткое отношение задано в виде:
Тогда носитель данного отношения будет иметь вид:
 . .
Опр. 6. Пусть на множестве  заданы два нечетких отношения заданы два нечетких отношения 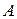 и и  с функциями принадлежности с функциями принадлежности 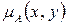 , ,  . Тогда множество . Тогда множество 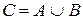 представляет собой объединение нечетких отношений представляет собой объединение нечетких отношений 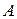 и и  на множестве на множестве  , если его функция принадлежности определяется выражением , если его функция принадлежности определяется выражением
 . .
Аналогично множество  является пересечением нечетких множеств является пересечением нечетких множеств 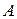 и и  , если , если
 . .
Пример 6. Даны отношения  и и  . Найти объединение и пересечение этих отношений. . Найти объединение и пересечение этих отношений.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.3
| 0.4
| 0.2
|
|
| 
| 0.3
|
| 0.7
|
| 
| 0.8
|
|
| 0.2
|
| 
| 0.1
| 0.8
|
|
| 
| 0.5
|
| 0.4
|
|
| 
| 0.6
| 0.9
| 0.3
| 0.2
| Результат:
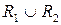
| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.3
| 0.4
| 0.7
|
|
| 
| 0.3
|
| 0.2
|
| 
| 0.8
|
|
|
|
| 
| 0.1
| 0.8
|
| 0.2
| 
| 0.6
| 0.9
| 0.4
| 0.2
|
| 
| 0.5
|
| 0.3
|
| Опр. 7. Нечеткое отношение  включает в себя (или содержит) нечеткое отношение включает в себя (или содержит) нечеткое отношение 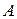 ( ( 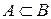 ), если для них выполняется соотношение ), если для них выполняется соотношение
 . .
Пример 7 Даны отношения  и и  . Проверить: . Проверить:  содержит содержит  ? ?

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.3
| 0.4
| 0.2
|
|
| 
| 0.4
| 0.4
| 0.2
| 0.1
| 
| 0.5
|
|
| 0.9
|
| 
| 0.5
|
|
|
| 
| 0.4
|
| 0.1
| 0.8
|
| 
| 0.5
| 0.1
| 0.2
| 0.9
| Ответ:  содержит содержит  . .
Задания:
Задача 1. Дано нечеткое отношение  в виде таблицы. Найти носитель в виде таблицы. Найти носитель  данного отношения (см. пример 5). данного отношения (см. пример 5).
Вариант 1.
|
| 
| 
| 
| 
| 
| 0.7
| 0.5
|
|
| 
|
| 0.8
|
| 0.75
| 
| 0.43
|
| 0.94
|
| Вариант 2.
|
| 
| 
| 
| 
| 
|
| 0.1
| 0.2
|
| 
| 0.3
|
| 0.4
| 0.5
| 
|
| 0.6
|
| 0.7
| Вариант 3.
|
| 
| 
| 
| 
| 
| 0.1
|
| 0.6
| 0.7
| 
|
| 0.4
| 0.5
|
| 
| 0.2
|
|
| 0.3
| Вариант 4.
|
| 
| 
| 
| 
| 
| 0.2
| 0.5
|
| 0.7
| 
|
|
| 0.4
| 0.9
| 
| 0.3
| 0.1
|
|
| Вариант 5.
|
| 
| 
| 
| 
| 
| 0.4
| 0.7
| 0.6
|
| 
| 0.9
|
|
| 0.3
| 
|
| 0.2
| 0.1
|
| Вариант 6.
|
| 
| 
| 
| 
| 
|
| 0.4
| 0.5
| 0.1
| 
|
|
| 0.2
| 0.7
| 
|
| 0.3
| 0.8
|
| Вариант 7.
|
| 
| 
| 
| 
| 
|
|
| 0.4
| 0.6
| 
| 0.1
|
|
| 0.2
| 
| 0.9
| 0.7
| 0.3
|
| Вариант 8.
|
| 
| 
| 
| 
| 
|
| 0.5
|
| 0.8
| 
|
| 0.4
| 0.7
|
| 
| 0.2
|
| 0.1
| 0.3
| Вариант 9.
|
| 
| 
| 
| 
| 
|
| 0.9
| 0.4
|
| 
| 0.3
|
|
| 0.97
| 
| 0.1
|
| 0.6
| 0.2
| Вариант 10.
|
| 
| 
| 
| 
| 
|
| 0.8
|
| 0.9
| 
| 0.2
|
| 0.5
| 0.1
| 
|
| 0.3
|
| 0.4
| Задача 2. Даны отношения  и и  . Найти объединение и пересечение этих отношений (см. пример 6). . Найти объединение и пересечение этих отношений (см. пример 6).
Вариант 1.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 0.1
| 0.2
| 0.3
|
| 
| 0.1
| 0.2
| 0.3
|
| 
| 0.5
| 0.4
|
| 0.7
|
| 
| 0.4
|
| 0.5
| 0.6
| 
| 0.6
|
|
| 0.8
|
| 
|
| 0.7
| 0.8
| 0.9
| Вариант 2.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.4
|
| 0.5
| 0.1
|
| 
| 0.9
|
| 0.8
| 0.7
| 
|
| 0.7
| 0.3
|
|
| 
| 0.4
| 0.5
| 0.6
|
| 
| 0.8
| 0.2
|
| 0.6
|
| 
| 0.3
| 0.2
|
| 0.1
| Вариант 3.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.3
| 0.8
|
|
|
| 
| 0.9
| 0.8
|
| 0.7
| 
| 0.7
|
| 0.6
| 0.4
|
| 
|
| 0.4
| 0.5
| 0.6
| 
|
| 0.5
| 0.1
| 0.2
|
| 
| 0.3
| 0.2
|
| 0.1
|
Вариант 4.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.6
|
| 0.7
|
|
| 
| 0.7
| 0.9
| 0.8
|
| 
| 0.8
| 0.1
|
| 0.5
|
| 
| 0.5
|
| 0.1
| 0.3
| 
| 0.2
|
| 0.4
| 0.3
|
| 
|
| 0.6
| 0.9
| 0.4
| Вариант 5.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 0.6
|
| 0.8
|
| 
| 0.3
|
| 0.4
|
| 
| 0.4
|
| 0.7
| 0.2
|
| 
| 0.2
| 0.7
| 0.5
| 0.9
| 
| 0.5
| 0.3
| 0.1
|
|
| 
| 0.8
| 0.1
|
| 0.6
| Вариант 6.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.8
| 0.7
| 0.5
|
|
| 
| 0.2
|
| 0.8
| 0.3
| 
|
| 0.2
| 0.6
| 0.3
|
| 
| 0.9
| 0.4
|
| 0.1
| 
| 0.1
|
| 0.4
|
|
| 
|
| 0.7
| 0.6
| 0.5
| Вариант 7.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 0.3
| 0.8
| 0.7
|
| 
|
| 0.3
| 0.4
|
| 
| 0.6
| 0.1
| 0.5
|
|
| 
| 0.8
| 0.1
|
| 0.2
| 
| 0.9
| 0.2
|
| 0.4
|
| 
| 0.6
| 0.9
| 0.5
| 0.7
| Вариант 8.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.8
|
| 0.3
| 0.1
|
| 
| 0.5
| 0.1
| 0.9
|
| 
|
| 0.7
| 0.5
| 0.8
|
| 
|
| 0.6
|
| 0.4
| 
| 0.6
| 0.4
| 0.2
|
|
| 
| 0.2
| 0.8
| 0.7
| 0.3
| Вариант 9.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
|
| 0.8
| 0.1
| 0.6
|
| 
|
| 0.7
| 0.1
| 0.6
| 
| 0.7
| 0.5
|
| 0.3
|
| 
| 0.2
| 0.5
|
| 0.9
| 
| 0.2
| 0.8
| 0.4
|
|
| 
| 0.4
| 0.3
| 0.8
|
| Вариант 10.

| 
| 
| 
| 
|
| 
| 
| 
| 
| 
| 
| 0.4
| 0.9
| 0.6
| 0.3
|
| 
| 0.8
|
| 0.6
| 0.2
| 
| 0.2
| 0.7
| 0.8
|
|
| 
| 0.3
| 0.1
| 0.9
|
| 
|
|
| 0.1
| 0.5
|
| 
|
| 0.7
| 0.5
| 0.4
| Задача 3. Даны отношения  и и  . Проверить: . Проверить:  содержит содержит  ? ?
Варианты взять из задачи № 2.
Нечеткие модели
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 на множестве
на множестве  называется некоторое подмножество декартова произведения
называется некоторое подмножество декартова произведения  .
. , которые связаны отношением
, которые связаны отношением  или
или  .
.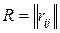 ,
,  ,
,  ,
,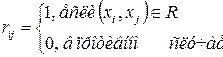

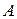 и
и  , множество
, множество  ,
, 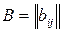 .
. , которое является объединением двух отношений:
, которое является объединением двух отношений:  .
.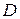 является пересечением отношений
является пересечением отношений 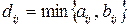 .
. и
и  выполняется условие
выполняется условие  .
.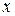 и
и  существует отношение
существует отношение 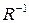 , что
, что 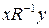 существует тогда и только тогда, когда
существует тогда и только тогда, когда  . Если при этом
. Если при этом 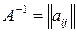 - матрицы этих отношений, то элементы этих матриц связаны соотношением:
- матрицы этих отношений, то элементы этих матриц связаны соотношением:  ,
,  .
.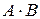 на декартовом произведении
на декартовом произведении  тогда и только тогда, когда существует такой
тогда и только тогда, когда существует такой 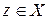 , для которого выполнены одновременно отношения
, для которого выполнены одновременно отношения  и
и  . При этом элементы матриц отношений связаны следующим образом:
. При этом элементы матриц отношений связаны следующим образом: .
.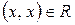 или
или  для любого
для любого  .
. (‘больше-равно’).
(‘больше-равно’). . В матрице рефлексивного отношения все диагональные элементы равны 1, а антирефлексивного – 0.
. В матрице рефлексивного отношения все диагональные элементы равны 1, а антирефлексивного – 0.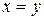 .
. .
. называется нечеткое подмножество декартова произведения
называется нечеткое подмножество декартова произведения  , которое характеризуется такой функцией принадлежности
, которое характеризуется такой функцией принадлежности  , что
, что  . Причем
. Причем  .
. -арное отношение есть нечеткое подмножество
-арное отношение есть нечеткое подмножество 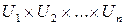 , причем:
, причем: .
.
 , где
, где  ;
;
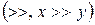 .
.
 из интервала
из интервала 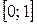 , связанные отношением
, связанные отношением  . Они образуют множество точек заштрихованной области, которые отделены четкой границей – диагональю от других точек.
. Они образуют множество точек заштрихованной области, которые отделены четкой границей – диагональю от других точек.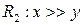 на единичном квадрате, убеждаемся, что существуют пары
на единичном квадрате, убеждаемся, что существуют пары  ), а также те, которые определенно не принадлежат
), а также те, которые определенно не принадлежат  ).
). ). Поэтому нечеткое множество
). Поэтому нечеткое множество  .
. ,
,  ,
, 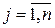 с элементами
с элементами  . Если
. Если  , то это означает, что степень выполнения отношения
, то это означает, что степень выполнения отношения 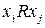 равна
равна  .
.
 . Отношение
. Отношение  можно задать функцией принадлежности
можно задать функцией принадлежности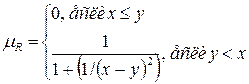
 ,
,  ,
, 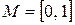 . Нечеткое отношение
. Нечеткое отношение 






 , при достаточно больших
, при достаточно больших  можно интерпретировать так: «
можно интерпретировать так: «  называется подмножество декартова произведения
называется подмножество декартова произведения  , определяемое как:
, определяемое как: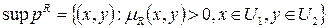
 .
.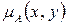 ,
,  . Тогда множество
. Тогда множество 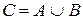 представляет собой объединение нечетких отношений
представляет собой объединение нечетких отношений  .
. является пересечением нечетких множеств
является пересечением нечетких множеств  .
.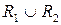

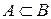 ), если для них выполняется соотношение
), если для них выполняется соотношение .
. данного отношения (см. пример 5).
данного отношения (см. пример 5).