
|
|
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций.Нормальное уравнение плоскости в векторной и координатной формах (вывод).
Положение плоскости в трехмерном пространстве будет вполне определено, если известно ее расстояние P от начала координат O, т.е. длина перпендикуляра ON, опущенного из точки O на плоскость, и единичный вектор  , перпендикулярный к плоскости. По условию, , перпендикулярный к плоскости. По условию,  . Для любой точки M(x,y,z), лежащей на плоскости, имеем (рисунок 4.11): . Для любой точки M(x,y,z), лежащей на плоскости, имеем (рисунок 4.11):
С другой стороны, по определению скалярного произведения двух векторов имеем:
Уравнение (4.36) называется векторным уравнением плоскости. Одновременно уравнение (4.36) называется нормальным уравнением плоскости. Пусть теперь единичный вектор
При этом уравнение (4.36) примет вид:
Уравнение (4.36) называется нормальным (нормированным) уравнением плоскости в координатной форме. Замечание: как и в случае нормального уравнения прямой, в рассматриваемом случае уравнение (4.37) можно получить, используя теорию проекций. 2. Общее уравнение плоскости Уравнение плоскости в отрезках.
Пусть плоскость не проходит через начало координат, а отсекает от осей координат соответственно отрезки a, b, c. Как видно из рисунка 4.10, плоскость проходит через точки M(a,0,0), N(0,b,0) и R(0,0,c). Рисунок 4.10Пусть общее уравнение плоскости имеет вид: Ax + By + Cz + D = 0 (4.31). Подставим в это уравнение координаты точек M, N и R, получим:
Так как плоскость не проходит через начало координат, то D≠ 0. Так как плоскость отсекает от осей координат ненулевые отрезки, то A≠ 0, B≠ 0, C≠ 0. Тогда из (4.34) имеем: Подставив эти значения в уравнение (4.31), получим: Так как D≠0, то все члены последнего равенства можно разделить на (-D). Получим:
Уравнение (4.35) и есть уравнение плоскости в отрезках. 3. Теоремы о пределах (вывод одной из них). Теорема 1. Для того, чтобы число A было пределом функции f(x) при x®a, необходимо и достаточно, чтобы эта функция была представлена в виде: f(x) = A+a(x), где a(x) – бесконечно малая функция. Теорема 2. Предел постоянной величины равен самой постоянной. Теорема 3. Если функция Теорема 4. Если функции
Доказательство. Ограничимся доказательством формулы (1). Пусть
Отсюда По свойству бесконечно малых (1) α(x) + β(x) – бесконечно малая, следовательно, по теореме (1):
Следствие 1. Если функция f(x) имеет предел при x → a, то:
Следствие 2. Постоянный множитель можно выносить за знак предела:
Теорема 5. Если для функций f(x), f1(x) и f2(x) в некоторой окружности точки a выполняется неравенство
4. Первый замечательный предел (вывод). Теорема. Доказательство. Возьмем круг единичного радиуса и положим Обозначим площади треугольника ОАВ через– S1, треугольника ОАС – S2, площадь сектора ОАВ – через S.
Неравенство (1) получено для
5.Производные элементарных функций (вывод одной из них).
Выведем формулу нахождения производной показательной функции Придавая аргументу
Переходим к пределу при
Правила дифференцирования суммы, произведения, частного (доказательство одного из них). Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций. Убедимся в этом для суммы двух функций (для большего числа слагаемых доказательство аналогичное). Пусть Отсюда, переходя к пределу при
2. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. Следствие1. Постоянный множитель можно выносить за знак производной: Следствие2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: 3. Производная частного двух дифференцируемых функций может быть найдена по формуле: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 или
или (4.36)
(4.36) образует с осями координат соответственно углы α, β, γ. Тогда
образует с осями координат соответственно углы α, β, γ. Тогда  . Далее, вектор
. Далее, вектор  . Тогда получим скалярное произведение векторов:
. Тогда получим скалярное произведение векторов: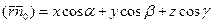
 (4.37)
(4.37)
 (4.34)
(4.34)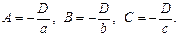
 .
. или
или  (4.35)
(4.35) ³0 (
³0 (  £0) для любых х в некоторой окрестности точки а, кроме быть может самой точки а, и в точке а имеет предел, то
£0) для любых х в некоторой окрестности точки а, кроме быть может самой точки а, и в точке а имеет предел, то 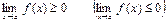
 и
и  имеют пределы при x®a, то при x®a имеют пределы их сумма
имеют пределы при x®a, то при x®a имеют пределы их сумма  произведение
произведение  и при условии, то
и при условии, то  частное
частное  причем
причем  (1)
(1) (2)
(2) (3)
(3) , тогда по теореме 1:
, тогда по теореме 1: где
где 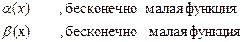
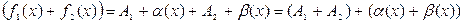
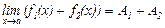 .
. , где n – натуральное число.
, где n – натуральное число. , c = const.
, c = const. , и
, и  , то
, то 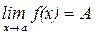

 (раскрывает неопределенность типа
(раскрывает неопределенность типа  ).
). . X – угол выраженный в радианах.
. X – угол выраженный в радианах.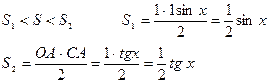
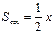


 однако cos x и
однако cos x и  функции четные ,т.к. cos (-x) = cos x.
функции четные ,т.к. cos (-x) = cos x. т.е. (1) справедливо и для
т.е. (1) справедливо и для 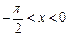 т.к.
т.к.  , то из (1) на основании теоремы 5 заключаем
, то из (1) на основании теоремы 5 заключаем  .
. 2.
2.  3.
3. 




 ,
,  :
: 
 ;
; 
 ;
;  2.
2. 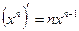 3.
3.  ;
;  4.
4.  ;
;  5.
5.  ;
;  6.
6.  ;
; 

 приращение
приращение  , находим для приращения функции
, находим для приращения функции  следующее значение:
следующее значение: (4.22). Делим на
(4.22). Делим на  (4.23)
(4.23) :
: , но
, но  . Поэтому
. Поэтому  (4.24). Итак
(4.24). Итак (4.25). В частности,
(4.25). В частности,  ).
). ; но тогда
; но тогда  . Деля на
. Деля на  .
. , находим (так как предел суммы равен сумме пределов):
, находим (так как предел суммы равен сумме пределов): или
или  .
. .
.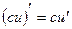 .
. .
. .
.