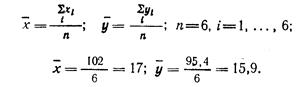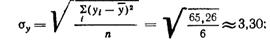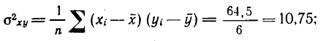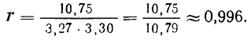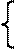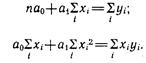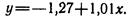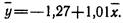|
|
МЕТОД КОРРЕЛЯЦИОННО-РЕГРЕССИОННОГО225-2008
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по изучению дисциплины "Методы моделирования производственных систем" и контрольные задания для студентов специальности 080502 "Экономика и управление на предприятии" заочной, вечерней форм обучения и экстерната
Воронеж 2008
Составитель: д-р экон. наук С.В. Амелин
УДК 658.512
Методические указания по изучению дисциплины "Методы моделирования производственных систем" и контрольные задания для студентов специальности 080502 "Экономика и управление на предприятии" заочной, вечерней форм обучения и экстерната / ГОУВПО "Воронежский государственный технический университет"; сост. С.В. Амелин. Воронеж, 2008. 39 с.
В методических указаниях приведены рабочая программа, вопросы для письменных ответов; варианты практических заданий и методические указания по их выполнению для студентов заочной, вечерней форм обучения и экстерната.
Табл. 6. Ил. 8. Библиогр.: 26 назв.
Рецензент канд. экон. наук, доц. Г.Н. Чернышова
Ответственный за выпуск зав. кафедрой д-р экон. наук, проф. О.Г. Туровец
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета ©ГОУВПО "Воронежский государственный технический университет", 2008 ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ Студенты должны ознакомится с программой и содержанием основных вопросов по дисциплине “Методы моделирования производственных систем”, внимательно изучить соответствующие методические указания и решение типовых задач. В процессе изучения дисциплины студенты письменно отвечают на вопросы. Выполняя контрольные задания, студенты должны показать ход решения, подробно изложить расчеты, расшифровать все используемые формулы, сделать краткие выводы. Изучая дисциплину “Методы моделирования производственных систем”, студенты выполняют тот вариант задания, номер которого соответствует последней цифре его шифра. Перед решением задачи необходимо ознакомиться с теоретическим материалом, соответствующего раздела дисциплины “Методы моделирования производственных систем”. ВОПРОСЫ ДЛЯ ПИСЬМЕННОГО ОТВЕТА 1. Как определяются понятия «модель» и «моделирование»? 2. Что собой представляет математическое моделирование производственных систем? 3. В чем заключается цель моделирования производственных систем? 4. В чем сущность системного подхода к моделированию производственных систем? 5. Что такое система и какие элементы составляют производственную систему? 6. В чём суть понятия «гомеостатическая система»? 7. Приведите основные этапы моделирования производственных систем. 8. Что называется гипотезой в моделировании систем? 9. Понятие аналогии в моделировании систем. 10. Раскройте содержание понятия «машинный эксперимент». 11. Какие существуют классификационные признаки видов моделирования систем? 12. Какие особенности характеризуют имитационное моделирование систем? 13. Чем определяется эффективность моделирования производственных систем на ЭВМ? 14. Что называется статической и динамической моделями производственной системы, и в каких случаях следует применять ту или иную модель? 15. В чем различие детерминированных и стохастических моделей производственных систем и когда применяются те или иные модели? 16. Что называется концептуальной моделью производственной системы? 17. Раскройте содержание понятия «черный ящик» при моделировании производственно-экономических систем? 18. Какова цель планирования машинных экспериментов? 19. Что называется полным и неполным факторным экспериментом? 20. Какие задачи можно решать на основе сетей Петри? 21. Что такое «переход» в сетях Петри и каковы правила срабатывания переходов? 22. В чем суть информационного подхода в моделировании производственных систем? 23. Что такое энтропия и как она изменяется при улучшении управляемости и организованности производственной системы? 24. Какие методы моделирования используются в перспективном планировании? 25. Какие методы моделирования используются в технико-экономическом управлении? 26. Какие методы моделирования используются в оперативном регулировании? 27. Какие методы моделирования используются при управлении вспомогательным производством? 28. Какие методы моделирования используются в управлении качеством продукции? 29. Какие методы моделирования используются в управлении НИР и ОКР? 30. Какие методы моделирования используются при технической подготовке производства? 31. Какие методы моделирования используются при оперативно-календарном планировании? 32. Какие методы моделирования используются в материально-техническом снабжении? 33. Какие методы моделирования используются в управлении кадрами? 34. Какие методы моделирования используются в управлении капитальным строительством? 35. Раскройте понятие «цели», дайте классификацию целей и каким образом можно применить моделирование при целепологании? 36. Раскройте содержание понятия «дерево целей». 37. В чем заключается сущность экспертных методов и какие задачи можно решать с их помощью? 38. Каким показателем определяется степень согласованности мнений экспертов и как его рассчитать? 39. Как подтвердить статистическую значимость показателя степени согласованности мнений экспертов? 40. Дайте определение понятию «структура» и какие методы можно использовать при моделировании структур производственных систем? 41. Раскройте содержание понятия «формализация производственно-экономических процессов и систем». 42. Какие критерии оптимальности используются при моделировании производственных систем? 43. Каковы различия между функциональной и корреляционной зависимостью? 44. Дайте определение понятиям «интерполяция», «аппроксимация» и «экстраполяция». 45. Приведите зависимости, используемые в экономике для аппроксимации опытных данных. 46. Какие задачи можно решать на основе корреляционно-регрессионного анализа? 47. В чем суть метода наименьших квадратов? 48. Как определяется, что показывает и для чего применяется коэффициент корреляции? 49. Что такое «тренд» и как это понятие используется в прогнозировании производственно-экономических процессов? 50. Дайте графическую интерпретацию и пояснения для коэффициентов линейного уравнения регрессии y =a0 +a1x. 51. Какие критерии оптимальности используются при моделировании структур производственных систем? 52. Раскройте понятие «обратная связь». Какая обратная связь применяется для стабилизации процесса, а какая для развития тенденции? Как смоделировать систему с обратной связью? 53. Что понимается под надёжностью производственной системы? Как определить надёжность системы, состоящей из последовательных и параллельно соединенных элементов? 54. Что понимается под параллельным и последовательным соединением элементов применительно к производственно-экономическим системам? 55. В чём суть метода анализа иерархий и назначение его использования? 56. Поясните суть принципа оптимальности в планировании и управлении с использованием моделей линейного программирования. 57. Сформулируйте общую постановку задачи линейного программирования и правила поиска оптимального решения графическим способом. 58. Каким образом проводится оценка адекватности и точности модели ? 59. Как применяется в моделировании метод Монте-Карло? 60. Какие языки имитационного моделирования вы знаете и в чем их отличия?
МОДЕЛИРОВАНИЕ СТРУКТУР ПРОИЗВОДСТВЕННЫХ СИСТЕМ При изучении методов моделирования структур производственных систем необходимо рассмотреть следующие вопросы: определение основных структурных характеристик; определение структурных параметров органов управления организации. При этом можно использовать следующую информацию. Моделирование формальной структуры ПС включает сбор информации, характеризующий её в статике (тип организационной структуры, распределение прав и обязанностей и т.п.), и изучение её в динамике (определение эффективности организационной структуры с позиций достижения конечных результатов деятельности). При моделировании организационной структуры большое значение имеет фиксирование формальных каналов коммуникаций, которые представляют интерес для рационального распределения функций и обязанностей в ходе подготовки и принятия решений. Необходимо изучать также неформальную структуру ПС. Сбор информации для моделирования ведется посредством наблюдения за групповыми и межличностными отношениями и их изменениями, проведения серий интервью, что дает возможность определить морально-психологический климат на предприятии. Информация собирается по подразделениям, отделам, у должностных лиц предприятия,- об их взаимодействии между собой, способах принятия и выполнения решений, их деятельность по обеспечению работоспособности предприятия. Информация для данной работы относится к «внутреннему» типу. Ее получение возможно частично из документов предприятия, а частично - в беседе с сотрудниками. Моделирование позволяет определять некоторые характеристики структуры ПС и давать им количественную оценку, оценивать качество структуры ПС и её элементов с позиций системного анализа, а также сравнивать различные варианты организационных структур между собой. Рассмотрим, например, линейно-функциональную структуру управления, в которой каждый структурный элемент (отдел, служба, производственное подразделение) выполняет конкретные задачи и обладает определенными правами и обязанностями.
Рис. 1. Организационная структура предприятия
Для проведения структурного анализа организационной структуры предприятия представим ее в виде графа G = {Х, U}, где Х - множество вершин (|Х| = n), соответствующее множеству структурных элементов; U - множество рёбер (|U| = m), соответствующее множеству связей между структурными элементами предприятия. Граф G, соответствующий данному предприятию, показан на рис. 5, где цифры обозначают: 1 - директор предприятия; 2 - зам. директора по производству; 3 - зам. директора по снабжению и сбыту; 4 - зам. директора по персоналу; 5 - главный бухгалтер; 6 - производственный отдел; 7 - производственные подразделения; 8 - отдел маркетинга; 9 - отдел материально-технического снабжения; 10 - отдел кадров; 11 - бухгалтерия.
Рис. 2. Структурный граф предприятия
1 - при наличии связи между элементами i и j, аij = 0 - при отсутствии связи.
Таблица 1 Матрица смежности
1. По матрице смежности определим ранг каждого элемента
где aij – элементы матрицы смежности, n – количество вершин (элементов) структуры. Например, r1 = 4 ∕20 = 0,2. Ранги структурных элементов приведены в последнем столбце табл. 1. Чем выше ранг элемента, тем более сильно он связан с другими элементами и тем более тяжёлыми будут последствия при потере качества его функционирования. В рассматриваемом случае наиболее высокий ранг (0,2) имеет первый элемент структуры (директор). 2. Проверим связность структуры. Для связных структур (не имеющих обрывов и висячих элементов) должно выполняться условие
где m – множество рёбер графа (½ от количества связей в матрице смежности). Правая часть неравенства определяет необходимое минимальное число связей в структуре графа, содержащего n вершин. Для нашего случая n (количество структурных элементов) равно 11 и условие (½)·20 = 11–1 выполняется, т.е. структура является связной. 3. Проведем оценку структурной избыточности R, отражающей превышение общего числа связей над минимально необходимым:
Данная характеристика является косвенной оценкой экономичности и надёжности исследуемой структуры и определяет принципиальную возможность функционирования и сохранения связей системы при отказе некоторых её элементов. Система с большей избыточностью R потенциально более надёжна, но менее экономична. Возможны три варианта: если R<0, то система несвязная; R = 0, система обладает минимальной избыточностью; R > 0, система имеет избыточность; чем выше R, тем выше избыточность. Для рассматриваемого случая R = [(½)·20∕ (11–1)] – 1 = 0, т.е. структура имеет минимальную избыточность. 4. Определим неравномерность распределения связей - Е. Данный показатель характеризует недоиспользование возможностей данной структуры, имеющей m рёбер и n вершин, в достижении максимальной связности. Величина Е определяется по формуле
где Для рассматриваемого случая Однако для сравнения различных структур по неравномерности связей используют относительную величину: Еотн= Е ∕ Еmax, где Еmах - максимальное значение неравномерности связей, которое достигается в системе, имеющей максимально возможное число вершин, имеющих одну связь. Величину Е определяют по эмпирической формуле
где y =m – n ; Для рассматриваемого случая y =10 – 11 = –1;
Тогда
Определим величину Е для рассматриваемого случая. Еотн = 3,41 ∕ 8,58 = 0,4. Величина Е для различных типов структур изменяется от 0 (для структур с равномерным распределением связей) до 1. В рассматриваемом случае распределение связей в структуре довольно равномерное. 5. Определим структурную компактность структуры Q, которая отражает общую структурную близость элементов между собой. Для этого используется формула
где dij - расстояние от элемента i до элемента j, т.е. минимальное число связей, соединяющих элементы i и j. Для определения величины общей структурной компактности построим матрицу расстояний D = ||dij|| - (табл. 2). По таблице определяем Q = 288. Таблица 2 Матрица расстояний D
Однако для количественной оценки структурной компактности и возможности объективного сравнения различных организационных структур чаще используют относительный показатель определяемый по формуле:
где Qmin = n ·(n –1) - минимальное значение компактности для структуры типа «полный граф» (каждый элемент соединен с каждым). Для нашей структуры Qmin = 11 · (11 –1) = 110. Тогда Qотн = 288 ∕110 –1 = 1,62. Структурную компактность можно характеризовать и другой характеристикой - диаметром структуры: d = mах dij, равным максимальному значению расстояния dij в матрице расстояний. Для рассматриваемой структуры d = 4. С увеличением Qотн и d увеличиваются средние временные задержки при обмене информацией между подразделениями, что вызывает снижение общей надёжности. С этой точки зрения, структура исследуемого предприятия имеет надёжность среднего уровня (максимальную надёжность имеет полный граф, для которого Qотн= 0, а d =1). 6. Для характеристики степени централизации системы используется показатель центральности структурного элемента:
который характеризует степень удаленности i-го элемента от других элементов структуры. Чем меньше удален i-й элемент от других, тем больше его центральность и тем большее количество связей осуществляется через него. В рассматриваемом случае наиболее центральным является первый элемент (директор), для которого Σdij = 16 = min, то есть он обладает максимальным коэффициентом центральности Zmах= 288 ∕ (2 · 16) = 9. Степень центральности в структуре в целом может быть охарактеризована индексом центральности:
Значение степени центральности находится в диапазоне 1≥δ≥0, при этом для структур с равномерным распределением связей δ = 0, для структур, имеющих максимальную степень централизации, δ = 1. Для рассматриваемого случая высокое значение степени центральности структуры (δ = 0,87) предъявляет высокие требования к пропускной способности центра (элемент 1), через который устанавливается большое число связей по приему и переработке информации, и надёжности его функционирования, так как отказ центрального элемента ведет к полному разрушению структуры. Данная методика оценки может быть использована при сравнительной оценке свойств структур ПС. С точки зрения топологии внутренних связей, выделяют следующие основные виды структур (рис. 6): а) последовательная; б) кольцевая; в) радиальная; г) древовидная; д) типа «полный граф»; е) несвязная. Рассмотрим применение количественных характеристик к анализу свойств этих структур. Результаты вычислений представлены в табл. 3. Таблица 3 Результаты сравнительного анализа
Рис. 3. Основные виды моделей структур
Из табл. 3 видно: 1) для несвязных структур R < 0; для структур без избы- точности (последовательное, радиальная, древовидная) R = 0; для структур с избыточностью по связям (кольцевая, полный граф) – R > 0; 2) наибольшую близость элементов (показатель Q) имеет структура типа «полный граф»; наименьшую - последовательная; радиальная и кольцевая структуры, неразличимые по показателю d, имеют различные значения Q; 3) радиальная и древовидная структуры, имеющие одинаковые или близкие значения R, Q, d, значительно отличаются по показателю δ, что соответствует физическому смыслу, ибо отход от полной централизации, характерной для радиальной структуры, ведет к большей равномерности распределения связей по элементам; 4) наивысшую неравномерность распределения связей (Е=1) имеет радиальная структура, а наименьшую (Е = 0) - кольцевая структура и полный граф. Анализируя значения структурных параметров, полученных в результате структурной диагностики, можно выявить основные недостатки структуры организации и внести некоторые коррективы в организационную структуру предприятия.
Задание. Рассмотрев предложенную организационную структуру проанализируйте её эффективность с использованием методов моделирования производственных систем
Варианты заданий:
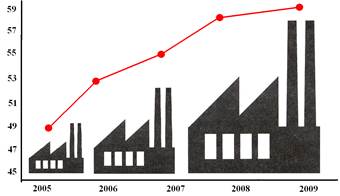
МЕТОД КОРРЕЛЯЦИОННО-РЕГРЕССИОННОГО АНАЛИЗА Метод корреляционного и регрессионного анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Теснота связи между изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэффициент корреляции. Одной из распространенных аналитических задач, решаемых с применением корреляционно метода, является задача на запуск-выпуск. Допустим, что имеются фактические данные о запуске и выпуске промышленных изделий (в тыс. шт.).
Требуется определить зависимость выпуска изделий в среднем от их запуска, составив соответствующее уравнение регрессии. По исходным данным построим в системе координат точки, соответствующие значениям переменных х и у. Проведем линию теоретической зависимости между показателями (рис.4).
Рис. 4. Линия регрессии Значения
Дальнейшим вычислениям придается табличная форма
Теснота связи между показателями запуска и выпуска измеряется коэффициентом корреляции, который исчисляется по формуле
Подставляя соответствующие значения, получим: выборочные средние квадратические отклонения
ковариация
парный коэффициент корреляции
Считая формулу связи линейной (у = а0 + а1х) определим зависимость выпуска промышленных изделий от их запуска. Для этого решается система нормальных уравнений:
Величины Σxi2 и Σxiyi представлены в следующей таблице
Значение а0 определяем из первого уравнения:
Подставляя найденное выражение а0 во второе уравнение, находим значение а1:
Итак, уравнение регрессии в окончательном виде получило следующий вид:
Проверка:
Коэффициент корреляции: Варианты заданий. По данным, представленным по вариантам, построить графическую зависимость между двумя показателями, определить уравнение регрессии и коэффициент корреляции. Проанализировать полученные результаты.
Вариант 1. Известны данные о количестве слесарей-ремонтников на машиностроительных заводах и данные о количестве станко-смен.
Вариант 2 В таблице приведены данные о численности работников по предприятиям.
Вариант 3 В таблице приведены данные анализа зависимости себестоимости 1 тонны угля от среднемесячной производительности труда рабочего на шахтах-комбинатах
Вариант 4 В таблице приведены данные о численности работников по предприятиям.
Вариант 5 Имеются данные по объему выпускаемой продукции и ее себестоимости.
Вариант 6 В таблице приведены данные о численности работников по предприятиям.
Вариант 7 В таблице приведены данные по выработке на одного работающего и фондовооружённость. Определить уравнение связи и корреляционное отношение.
Вариант 8 В таблице приведены данные о численности работников по предприятиям связи.
Вариант 9 Известны данные о количестве слесарей-ремонтников на машиностроительных заводах и данные о количестве единиц ремонтной сложности. Данные приведены в таблице.
Вариант 10. В таблице приведены данные о численности работников по предприятиям. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|


 Для описания графа G построим матрицу смежности (табл. 1), которая для неориентированного графа имеет вид А = ||аij||, где аij - элементы матрицы смежности, определяемые следующим образом:
Для описания графа G построим матрицу смежности (табл. 1), которая для неориентированного графа имеет вид А = ||аij||, где аij - элементы матрицы смежности, определяемые следующим образом: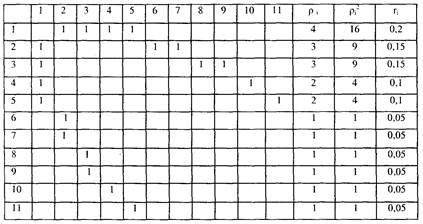


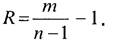

 - вес i-го элемента, или количество связей i- го элемента со всеми остальными.
- вес i-го элемента, или количество связей i- го элемента со всеми остальными.
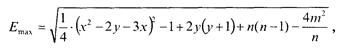
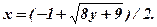

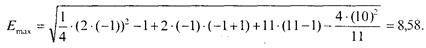



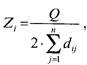






 и
и  определяются по формулам:
определяются по формулам: