
|
|
Безударное сжатие газа. Движение с однородной деформацией.
Задача о поршне, несмотря на относительную простоту, находит применение во многих проблемах, связанных с быстропротекающими процессами в сжимаемых средах. Так, например, движение среды, возникающее при взрыве, можно приближенно описывать, моделируя границу области, занятой продуктами взрыва, расширяющимся поршнем. Изучение установившегося гиперзвукового обтекания летательных аппаратов и других тонких тел с использованием «закона плоских сечений» [Ильюшин, Черный] сводится к рассмотрению нестационарного течения газа, вызванного расширяющимся цилиндрическим поршнем. Проблема осуществления быстрого и сильного сжатия некоторого материального объема также может рассматриваться с использованием решения газодинамической задачи о поршне. Подобные задачи актуальны, например, в связи с проблемой управляемого термоядерного синтеза. Для того, чтобы инициировать реакцию синтеза ядер, нужно сжать термоядерную «мишень» до очень высоких значений плотности при температуре в несколько миллионов градусов. Конечно, в указанных проблемах следует рассматривать сферический, цилиндрический или, вообще, неодномерный поршень. Для простоты, мы ограничимся изучением лишь задачи о плоском поршне. Следует отметить, однако, что многие качественные выводы могут быть перенесены с этого простейшего частного случая на более общие. Рассмотрим задачу о плоском поршне, который движется с нулевой начальной скоростью в сторону области, занятой однородным покоящимся газом. Исследуем случай, когда момент наступления градиентной катастрофы Как и для выдвигающегося из газа поршня, возникающее течение представляет собой простую волну (3.2). Однако теперь это будет волна сжатия (а не разрежения), в которой прямолинейные характеристики семейства C+ образуют сходящийся веер. В случае совершенного газа с постоянными теплоемкостями решение строится точно так же, как и в предыдущем параграфе: конкретный вид функции f(v) из (3.2) определяется законом движения поршня xП=xП(t) . Если провести огибающую L семейства прямолинейных C+- характеристик в плоскости (x; t) , то момент
Начиная с момента Особый интерес представляет случай, когда точка (
В этом случае имеем мгновенное "превращение" слабого разрыва (каким является фронт ВР) в сильный разрыв – ударную волну. Наглядно такой процесс иллюстрируется графиком зависимости давления p от координаты x в следующие друг за другом моменты времени (рис. ).
Подбирая нужным образом закон движения поршня xП(t) , можно добиться сколь угодно сильного сжатия газа в простой волне. Например, ситуации, показанной на рис. , отвечает сжатие в центрированной простой волне (с центром в точке Здесь мы имеет дело с безударным изоэнтропическим сжатием газа поршня [Овсянников].
Другой интересный пример безударного сжатия конечного объема газа до сколь угодно больших значений плотности и давления может быть описан в классе решений с однородной деформацией. [Седов "Методы подобия"]. В отличие от предыдущего рассмотрения, не будет предполагать постоянства плотности и давления в начальный момент времени. Движением с однородной деформацией в газовой динамике называют такое течение газа, в котором скорость является в любой момент времени линейной однородной функцией прямоугольных декартовых координат
Тогда тензор скоростей деформаций зависит только от времени и не зависит от координат частицы среды:
Если связь между эйлеровыми и лагранжевыми координатами имеет вид
то компоненты скорости определяется из равенств
где Тогда условие (5.1) выполняется, если положить
Рассмотрим частный случай – одномерное движение газа с однородной деформацией. Тогда матрица
Первый вариант соответствует движению газа с плоскими волнами ( ν=1 ), второй – движению с цилиндрическими волнами ( ν=2 ), третий – движению со сферическими волнами ( ν=3 ). Закон движения сплошной среды имеет в этом случае вид (x - эйлерова, ξ - лагранжева координата)
а скорость оказывается пропорциональной координате:
Запишем уравнение неразрывности в переменных Лагранжа [Седов]:
Учитывая, что в рассматриваемом случае
получаем
При непрерывном адиабатическом движении совершенного газа с показателем адиабаты γ значение отношения p/ργ в любой частице с течением времени не меняется. Поэтому давление может быть выражено в виде
Воспользуемся теперь уравнением импульсов (1.2). Сначала преобразуем участвующие в нем слагаемые:
В силу (1.2), получаем равенство
Разделяя переменные, приходим к системе
Интегрируя первое уравнение, получаем
Второе уравнение легко интегрируется, если обе его части умножить на
Извлекая квадратный корень и интегрируя еще раз, получаем в неявной форме зависимость R(t) :
Найденное частное решение уравнений газовой динамики содержит одну произвольную функцию лагранжевой координаты ρ0(ξ) и произвольные постоянные: p0(ξ0) , C , A , R0 . Этим решением может быть описан, например, разлет газового облака в вакуум либо процесс сжатия некоторого объема газа изменяющимся во времени внешним давлением. Первому случаю отвечает условие C < 0, A > 0, а второму - C > 0 . В частности, если положить ρ0(ξ)≡ρ0=const , то согласно (5.9) зависимость давления от координаты будет квадратичной:
При C > 0 давление растет с удалением от центра, а при C < 0 - падает и обращается в нуль, если Характер движения границы газового объема определяется уравнениями (5.3), (5.11), где нужно положить ξ= ξгр. . При разлете в вакуум скорость движения границы асимптотически (при t → ∞) стремится к постоянному значению Если конечный газовый объем сжимается из состояния покоя растущим во времени внешним давлением ( C > 0 ), то за время
где R0 - корень уравнения ЛИТЕРАТУРА 1. Черный Г.Г. Газовая динамика. – М.: Наука, 1988. 2. Овсянников Л.В. Лекции по основам газовой динамики. – Москва-Ижевск: Институт компьютерных исследований, 2003. 3. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика (в 10 т.). Т. VI. Гидродинамика. – М.: Наука, 1986. 4. Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений и их приложения к газовой динамике. – М.: Наука, 1978. 5. Седов Л.И. Методы подобия и размерности в механике. – М.: Наука, 1987. 6. Галин Г.Я., Голубятников А.Н., Каменярж Я.А. и др. Механика сплошных сред в задачах. В 2-х томах (Под ред. Эглит М.Э.) – М.: «Московский Лицей», 1996. 7. Уизем Дж. Линейные и нелинейные волны. – М.: Мир, 1977. 8. Колоколов И.В., Кузнецов Е.А., Мильштейн А.И. и др. Задачи по математическим методам физики. – М.: КомКнига, 2007. 9. Атанов Г.А. Газовая динамика. – К.: Выща шк., 1991. 10. Курант Р., Фридрихс К. Сверхзвуковое течение и ударные волны.- М.: Изд-во иностранной литературы, 1950. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 отличен от начального t0=0 .
отличен от начального t0=0 . точки на линии L с минимальной t-координатой (рис. ) [Черный; Ландау, Лифшиц].
точки на линии L с минимальной t-координатой (рис. ) [Черный; Ландау, Лифшиц].



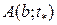 ) до бесконечного давления и бесконечной плотности газа, занимавшего первоначально область
) до бесконечного давления и бесконечной плотности газа, занимавшего первоначально область  .
.
 (5.1)
(5.1)
 i = 1, 2, 3, (5.2)
i = 1, 2, 3, (5.2)
 – элементы матрицы, обратной к
– элементы матрицы, обратной к  .
.
 представима в одной из трех форм
представима в одной из трех форм
 (5.3)
(5.3)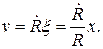 (5.4)
(5.4)

 (5.5)
(5.5) (5.6)
(5.6)

 (5.7)
(5.7) (5.8)
(5.8) (5.9)
(5.9) :
: (5.10)
(5.10) (5.11)
(5.11)
 (этому значению лагранжевой координаты отвечает граница между газом и вакуумом).
(этому значению лагранжевой координаты отвечает граница между газом и вакуумом). Это видно из (5.4), (5.10), поскольку ν(1-γ) < 0 и поэтому
Это видно из (5.4), (5.10), поскольку ν(1-γ) < 0 и поэтому  при R → ∞ .
при R → ∞ . ,
, =0 , все частицы оказываются в центре x=0 , а плотность и давление обращаются в бесконечность: происходит коллапс газового облака. В момент схлопывания внешнее давление тоже становится бесконечно большим.
=0 , все частицы оказываются в центре x=0 , а плотность и давление обращаются в бесконечность: происходит коллапс газового облака. В момент схлопывания внешнее давление тоже становится бесконечно большим.