
|
|
Применение дифференциала к приближенным вычислениям.
По аналогии с линеаризацией функции одной переменной можно при приближенном вычислении значений функции нескольких переменных, дифференцируемой в некоторой точке, заменять ее приращение дифференциалом. Таким образом, можно находить приближенное значение функции нескольких (например, двух) переменных по формуле:
где Пример. Вычислить приближенное значение Рассмотрим функцию
Дифференцирование сложных функций. Пусть аргументы функции z = f (x, y) являются, в свою очередь, функциями переменных u и v: x = x (u, v), y = y (u, v). Тогда функция f тоже есть функция от u и v. Выясним, как найти ее частные производные по аргументам u и v, не делая непосредственной подстановки z = f ( x(u, v), y(u, v)). При этом будем предполагать, что все рассматриваемые функции имеют частные производные по всем своим аргументам. Зададим аргументу u приращение Δ u, не изменяя аргумент v. Тогда
Если же задать приращение только аргументу v, получим: Разделим обе части равенства (2.7) на Δu, а равенства (2.8) – на Δv и перейдем к пределу соответственно при Δu→0 и Δv→0. Учтем при этом, что в силу непрерывности функций х и у
Рассмотрим некоторые частные случаи. Пусть x = x(t), y = y(t). Тогда функция f (x,y) является фактически функцией одной переменной t , и можно, используя формулы (2.9) и заменяя в них частные производные х и у по u и v на обычные производные по t (разумеется, при условии дифференцируемости функций x(t) и y(t) ) , получить выражение для
Предположим теперь, что в качестве t выступает переменная х, то есть х и у связаны соотношением у = у (х). При этом, как и в предыдущем случае, функция f является функцией одной переменной х. Используя формулу (2.10) при t = x и учитывая, что
Обратим внимание на то, что в этой формуле присутствуют две производные функции f по аргументу х: слева стоит так называемая полная производная, в отличие от частной, стоящей справа. Примеры. 1. Пусть z = xy, где x = u² + v, y = uv². Найдем
(В окончательный результат подставляем выражения для х и у как функций u и v). 2. Найдем полную производную функции z = sin (x + y²), где y = cos x.
Инвариантность формы дифференциала. Воспользовавшись формулами (2.5) и (2.9), выразим полный дифференциал функции z = f (x, y) , где x = x(u,v), y = y(u,v), через дифференциалы переменных u и v:
Следовательно, форма записи дифференциала сохраняется для аргументов u и v такой же, как и для функций этих аргументов х и у, то есть является инвариантной (неизменной).
Неявные функции, условия их существования. Дифференцирование неявных функций. Частные производные и дифференциалы высших порядков, их свойства.
Определение 3.1. Функция у от х, определяемая уравнением F (x, y) = 0 , (3.1) называется неявной функцией.
Конечно, далеко не каждое уравнение вида (3.1) определяет у как однозначную (и, тем более, непрерывную) функцию от х. Например, уравнение эллипса
задает у как двузначную функцию от х: Условия существования однозначной и непрерывной неявной функции определяются следующей теоремой: Теорема 3.1 (без доказательства). Пусть: 1) функция F (x,y) определена и непрерывна в некотором прямоугольнике 2) F (x0 , y0 ) = 0 ; 3) при постоянном х F (x,y) монотонно возрастает (или убывает) с возрастанием у. Тогда а) в некоторой окрестности точки (х0 , у0 ) уравнение (3.1) определяет у как однозначную функцию от х: y = f(x); б) при х = х0 эта функция принимает значение у0 : f (x0) = y0 ; в) функция f (x) непрерывна.
Найдем при выполнении указанных условий производную функции y = f (x) по х. Теорема 3.2. Пусть функция у от х задается неявно уравнением (3.1), где функция F (x,y) удовлетворяет условиям теоремы 3.1. Пусть, кроме того,
Пример. Найдем Тогда из формулы (3.2) получаем:
Производные и дифференциалы высших порядков. Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:
Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:
Определение 3.2. Частной производной n-го порядкафункции нескольких переменных называется первая производная от производной (n – 1)-го порядка.
Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например, Теорема 3.3. Если функция z = f (x,y) и ее частные производные
Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (2.6)
, (2.6)
 .
. и выберем х0 =1, у0 = 2. Тогда Δх = 1,02 – 1 = 0,02; Δу = 1,97 – 2 = -0,03. Найдем
и выберем х0 =1, у0 = 2. Тогда Δх = 1,02 – 1 = 0,02; Δу = 1,97 – 2 = -0,03. Найдем  ,
, Следовательно, учитывая, что f (1, 2) = 3, получим:
Следовательно, учитывая, что f (1, 2) = 3, получим:
 . (2.7)
. (2.7) . (2.8)
. (2.8) . Следовательно,
. Следовательно, (2.9)
(2.9) :
: (2.10)
(2.10) , получим, что
, получим, что . (2.11)
. (2.11) и
и  . Для этого предварительно вычислим частные производные трех заданных функций по каждому из своих аргументов:
. Для этого предварительно вычислим частные производные трех заданных функций по каждому из своих аргументов: Тогда из формулы (2.9) получим:
Тогда из формулы (2.9) получим: 

 (2.12)
(2.12)
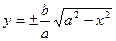 для
для 
 с центром в точке (х0 , у0 );
с центром в точке (х0 , у0 ); - непрерывные функции в некоторой области D, содержащей точку (х,у), координаты которой удовлетворяют уравнению (3.1), причем в этой точке
- непрерывные функции в некоторой области D, содержащей точку (х,у), координаты которой удовлетворяют уравнению (3.1), причем в этой точке  . Тогда функция у от х имеет производную
. Тогда функция у от х имеет производную (3.2)
(3.2) , если
, если  . Найдем
. Найдем  ,
,  .
. .
.
 ). Докажем это утверждение.
). Докажем это утверждение. определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке
определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке