
|
|
Свойства пределов и непрерывных функций.Геометрическое изображение функции двух переменных.
Рассмотрим функцию z = f(x,y), (1.1) определенную в некоторой области М на плоскости Оху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где
z = f(x,y)
Линии и поверхности уровня.
Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня. Пример. Найдем линии уровня для поверхности z = 4 – x² - y². Их уравнения имеют вид x² + y² = 4 – c (c=const) – уравнения концентрических окружностей с центром в начале координат и с радиусами
Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня. Пример. Для функции u = 3x + 5y – 7z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y – 7z –12 + с = 0.
Предел и непрерывность функции нескольких переменных.
Введем понятие δ-окрестности точки М0 (х0 , у0) на плоскости Оху как круга радиуса δ с центром в данной точке. Аналогично можно определить δ-окрестность в трехмерном пространстве как шар радиуса δ с центром в точке М0 (х0 , у0 , z0). Для n-мерного пространства будем называть δ-окрестностью точки М0 множество точек М с координатами
где Определение 1.4. Число А называется пределом функции нескольких переменных f Обозначения: Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри δ-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых повторных пределов, получаемых последовательными предельными переходами по каждому аргументу в отдельности. Примеры. 1. Покажем, что функция 2. Найдем повторные пределы функции
Замечание. Можно доказать, что из существования предела в данной точке в обычном смысле и существования в этой точке пределов по отдельным аргументам следует существование и равенство повторных пределов. Обратное утверждение неверно.
Определение 1.5. Функция f Если ввести обозначения
Определение 1.6. Внутренняя точка М0 области определения функции z = f (M) называется точкой разрыва функции, если в этой точке не выполняются условия (1.2), (1.3). Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве линииили поверхности разрыва. Примеры. 1. Функция z = x² + y² непрерывна в любой точке плоскости Оху. Действительно, 2. Единственной точкой разрыва функции 3. Для функции
Свойства пределов и непрерывных функций.
Так как определения предела и непрерывности для функции нескольких переменных практически совпадает с соответствующими определениями для функции одной переменной, то для функций нескольких переменных сохраняются все свойства пределов и непрерывных функций, доказанные в первой части курса, а именно: 1) Если существуют 2) Если 3) Если функции f(M) и g(M) непрерывны в точке М0, то в этой точке непрерывны и функции f(M) + g(M), kf(M), f(M)•g(M), f(M)/g(M) (если g(M0) ≠ 0). 4) Если функции
5) Функция 6) Если функция 7) Если функция
Частные производные. Рассмотрим изменение функции Определение 1.7. Частной производной функции Обозначения: Таким образом, частная производная функции нескольких переменных определяется фактически как производная функции одной переменной – хi. Поэтому для нее справедливы все свойства производных, доказанные для функции одной переменной. Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными. Примеры. 1. z = 2x² + 3xy –12y² + 5x – 4y +2, 2. z = xy, 3.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.
, является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.




 z
z 
 M y
M y

 Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n-мерном пространстве», хотя изобразить подобную поверхность невозможно.
Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n-мерном пространстве», хотя изобразить подобную поверхность невозможно. . Например, при с=0 получаем окружность x² + y² = 4 .
. Например, при с=0 получаем окружность x² + y² = 4 . , удовлетворяющими условию
, удовлетворяющими условию
 - координаты точки М0. Иногда это множество называют «шаром» в n-мерном пространстве.
- координаты точки М0. Иногда это множество называют «шаром» в n-мерном пространстве.
 такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0.
такое, что | f(M) – A| < ε для любой точки М из δ-окрестности М0. .
.
 не имеет предела при М→О(0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой
не имеет предела при М→О(0,0). Действительно, если в качестве линии, по которой точка М приближается к началу координат, выбрать прямую у = х, то на этой прямой  . Если же траекторией движения считать прямую у = 2х, то
. Если же траекторией движения считать прямую у = 2х, то 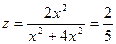 . Следовательно, предел в точке (0,0) не существует.
. Следовательно, предел в точке (0,0) не существует. при х→0, у→0.
при х→0, у→0. 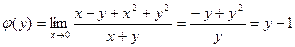 ,
,  . Если же произвести предельные переходы в обратном порядке, получим:
. Если же произвести предельные переходы в обратном порядке, получим: 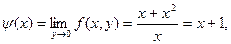
 Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле).
Таким образом, повторные пределы оказались различными (откуда следует, конечно, что функция не имеет в точке (0,0) предела в обычном смысле). (1.2)
(1.2) , то условие (1.2) можно переписать в форме
, то условие (1.2) можно переписать в форме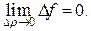 (1.3)
(1.3) , поэтому
, поэтому  .
. является точка (0,0).
является точка (0,0). то существуют и
то существуют и 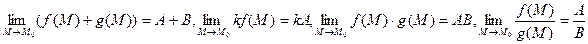 (если
(если  ).
).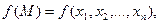 а
а  и для любого i существуют пределы
и для любого i существуют пределы  и существует
и существует  , где М0
, где М0  при
при  , где
, где 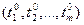 - координаты точки Р0.
- координаты точки Р0. непрерывны в точке Р0
непрерывны в точке Р0  непрерывна в точке М0
непрерывна в точке М0  , то сложная функция
, то сложная функция .
. .
. .
.

