
|
|
Вычисление предела функции методом непосредственной подстановкиПримеры: 1. Найти Решение: 1 способ. Применяя теоремы о пределах с последующей подстановкой предельного значения x=1 запишем:
2 способ. Поскольку исходная функция есть алгебраическая сумма элементарных функций, непрерывных в области определения, а, следовательно, и при x=1, то согласно определению непрерывности функции
Ответ: 2. Найти Решение: При x→3 числитель дроби стремится к числу 4, а знаменатель к числу 2.
Следовательно, применяя теоремы о пределах с последующей подстановкой предельного значения x=3 можно записать
Ответ: 2 3. Найти Решение: При x→2 числитель дроби стремится к 0, а знаменатель к числу 10
Следовательно, применяя теоремы о пределах с последующей подстановкой предельного значения x=2 можно записать
Ответ: 0 III. МЕТОДЫ РАСКРЫТИЯ НЕОПРЕДЕЛЕННОСТЕЙ
При решении заданий на вычисление предела функции одной переменной встречаются различные виды неопределенностей. А именно: неопределенность вида Различные виды неопределенностей имеют свои методы раскрытия. 3.1. Неопределенность вида Разложение числителя и знаменателя на множители с последующим сокращением Примеры: 1. Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Для квадратного трёхчлена Где Для 3x2+x-4 получим:
Для
Тогда
Ответ: -7 2. Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Для квадратного трёхчлена:
где Для
Числитель разложим на множители следующим образом: Тогда Ответ: 3. Найти Решение: При непосредственной подстановке предельного значения x=3 числитель и знаменатель обращаются в нуль
Имеем неопределённость вида Для квадратного трёхчлена
где Для
Знаменатель разложим по формуле
Для Тогда Ответ:
Деление многочлена на многочлен 1. Найти Решение:
2x²-2x 3x²-3 -(2x²-2x) -(3x²-3x)
0 3x-3 -(3x-3)
Разложим числитель и знаменатель на множители и сократим дробь:
Вычислим предел:
Ответ: Устранение иррациональных разностей домножением на сопряженное выражение Примеры: 1. Найти Решение: При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида А затем при наличии общего множителя сократим на него дробь.
2. Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида
3. Найти Решение: При непосредственной подстановке предельного значения x=0 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида
Ответ: Замена переменной Пример: Найти Решение: При непосредственной подстановке предельного значения x=1 числитель и знаменатель обращаются в нуль.
Имеем неопределённость вида Затем после преобразований сократим дробь на общий множитель.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
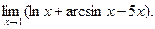
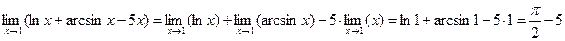
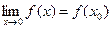 имеем
имеем



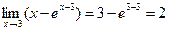

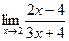



 ,
, 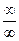 ,
, 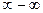 ,
,  ,
, 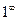 .
.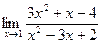
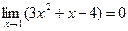
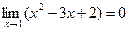

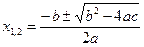


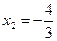
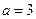
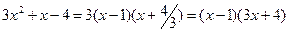
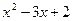 получим:
получим: 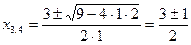
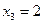
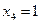
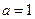

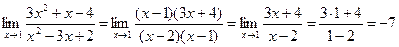
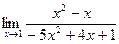


 получим:
получим: 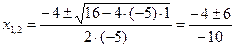
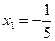
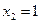


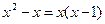

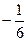
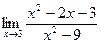
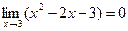
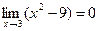
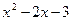 получим:
получим: 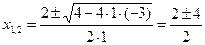
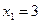
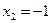
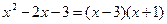
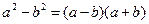
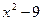 получим:
получим: 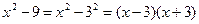
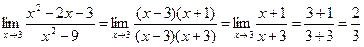
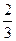
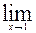
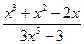
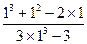 =
= 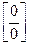 -неопределенность, для раскрытия требуется дробь сократить.
-неопределенность, для раскрытия требуется дробь сократить. Так как x=1 – корень многочленов, то многочлены кратны одночлену (x – 1):
Так как x=1 – корень многочленов, то многочлены кратны одночлену (x – 1):
 -(x³-x²) x²+2x -(3x³-3x²) 3x²+3x+3
-(x³-x²) x²+2x -(3x³-3x²) 3x²+3x+3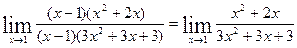
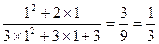 .
.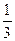


 для раскрытия неопределённости домножим числитель и знаменатель на сопряжённый двучлен
для раскрытия неопределённости домножим числитель и знаменатель на сопряжённый двучлен 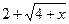 ,
,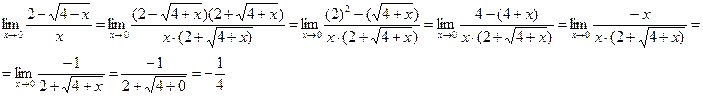 Ответ:
Ответ: 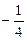
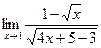
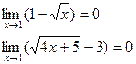
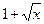 и
и 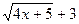 , а затем при наличии общего множителя сократим на него дробь
, а затем при наличии общего множителя сократим на него дробь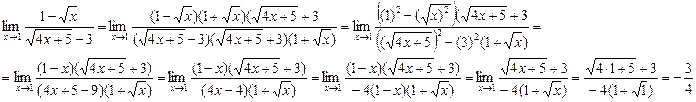 Ответ:
Ответ: 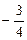

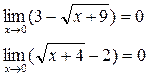
 и
и 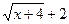 , а затем при наличии общего множителя сократим на него дробь.
, а затем при наличии общего множителя сократим на него дробь.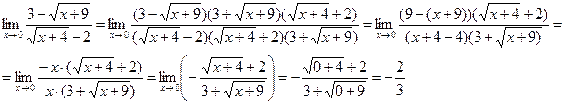




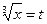 (x=t3). Тогда при
(x=t3). Тогда при 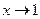
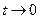 .
.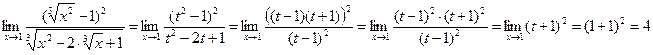 Ответ: 4
Ответ: 4