
|
|
Изложите вывод уравнений Лагранжа II рода в случае потенциального поля сил. Что такое функция Лагранжа.Если силы пот.: Ф-ция, равная разности кин. и пот. энергий механической системы, наз. ф-цией Лагранжа, или кинетическим потенциалом: Основы теории малых колебаний около положения устойчивого равновесия. Сформулировать теорему Лагранжа–Дирихле. - Механическая система может совершать малые колебания только около положения устойчивого равновесия.
- Положение системы называется положением равновесия, если в начальный момент времени система была приведена в это положение при нулевых скоростях и всё время остаётся в этом положении.
- Положение равновесия системы бывает: устойчивым, неустойчивым, безразличным.
- Под устойчивостью мех. сист. подразумевается такое ее свойство, когда все величины, определяющие ее состояние, при малых возмущениях остаются вблизи тех их значений, которые характеризуют невозмущенное состояние системы.
Л-Д: Если в некотором положении консервативной механической системы потенциальная энергия имеет строгий минимум, то это положение является положением устойчивого равновесия системы.
Доказать приближенную формулу кинетической энергия системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия. Система, на которую наложены голономные, идеальные удерживающие и стационарные связи, состоит из N материальных точек и движется около положения устойчивого равновесия системы, где Кинетическая энергия системы: Радиус-вектор Разложим функцию A(q) в окрестности положения равновесия (
Все величины вычислены при
Доказать приближенную формулу потенциальной энергия системы с одной степенью свободы при малых отклонениях от положения устойчивого равновесия. Система, на которую наложены голономные, идеальные удерживающие и стационарные связи, состоит из N материальных точек и движется около положения устойчивого равновесия системы, где Разложим потенциальную энергию в степенной ряд в окрестности положения равновесия
1-ый член в разложении (1) равен нулю, так как потенциальная энергия в положении равновесия равна нулю. 2-ой член в этом разложении равен обобщенной силе, которая в положении равновесия также равна нулю. В силу малости колебаний потенциальная энергия должна содержать члены не выше II порядка. Тогда: Коэфф. при второй степени обобщенной координаты обозначим через «с» - обобщенный коэфф. жесткости. С учетом введенного обозначения:
Вывести дифференциальное уравнение свободных колебаний механической системы с одной степенью свободы. Изложить его решение. Дать определение изохронизма свободных колебаний. - Определяем положение системы обобщенной координатой q, при равновесии Уравнение Лагранжа II рода: Так как равновесие устойчиво, а возмущения малы, для Т и П воспользуемся выражениями: Подставляя (2) в уравнение (1), получим:
Характеристическое уравнение:
Постоянные Частным решением уравнения (3), которое соотв. начальным условиям будет: Приведем решение к амплитудной форме: - Величина периода, как и круговая частота, не зависят от начальных условий, а определяются только свойствами колеблющейся системы, то есть коэффициентом инерции и коэффициентом жесткости. Независимость периода и частоты колебаний от начальных условий называется изохронностью колебаний. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
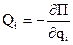 (
(  ), ур-я Лагранжа примут вид:
), ур-я Лагранжа примут вид: 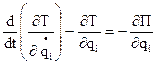 (
(  (
( 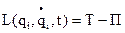 (
(  (
(  .
.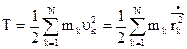 .
. каждой точки системы зависит только от обобщенной координаты q(t):
каждой точки системы зависит только от обобщенной координаты q(t):  .
.  , следовательно, кинетическая энергия равна:
, следовательно, кинетическая энергия равна:  (1).
(1).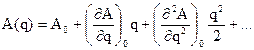 (2).
(2). , то в разложении (2) удержим только первый постоянный член, который обозначим «a». Приближенное выражение кинетической энергии:
, то в разложении (2) удержим только первый постоянный член, который обозначим «a». Приближенное выражение кинетической энергии:  . «а» - коэфф. инерции.
. «а» - коэфф. инерции. 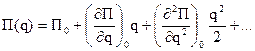 (1).
(1). .
. .
. (1).
(1).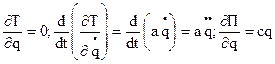 (2).
(2).
 , где:
, где:  = const, круговая или циклическая частота, которая имеет размерность угловой скорости (
= const, круговая или циклическая частота, которая имеет размерность угловой скорости ( 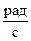 ).
).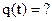
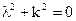
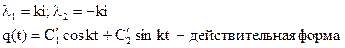
 и
и 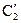 определяем из начальных условий:
определяем из начальных условий: 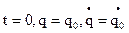 .
. .
.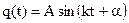 - закон движения системы.
- закон движения системы.