
|
|
Сформулируйте принцип возможных перемещений и докажите его необходимость.Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю. Доказательство необходимости: Система мат. точек, удовл. принципу возможных перемещений, наход. в равновесии. Докажем, что выполн. равенство: Просуммирует по k и раскроем скобки:
Сформулируйте принцип возможных перемещений и докажите его достаточность. Для равновесия механической системы, на которую наложены голономные, стационарные, удерживающие и идеальные связи, необходимо и достаточно, чтобы сумма работ всех активных сил, приложенных к точкам системы, на любом возможном перемещении системы равнялась нулю. Доказательство достаточности: Выполняется равенство От противного: (1) выполняется, но система в равновесии не находиться. Это означает, что система под действием активных сил и сил реакций за малый промежуток времени совершит некоторое действ. перемещ. На этом действ. перемещ. Докажите условия равновесия механической системы в обобщенных координатах. На систему из N материальных точек наложены связи, удовл. принципу возможных перемещений. Запишем: Изложите вывод принципа Даламбера–Лагранжа (общего уравнения динамики), сформулируйте его и запишите соответствующие формулы в векторной и аналитической формах. На голономную систему наложены удерживающие и идеальные связи. Применим к системе принцип Даламбера. Такая система сил, будет удовлетворять условию: Зафиксируем время и сообщим точкам возможные перемещ. При любом движении механической системы с идеальными и удерживающими связями в каждый данный момент сумма возможных работ всех активных сил и сил инерции на любом возможном перемещении равна нулю. В проекциях на декартовы оси координат:
Запишите уравнения Лагранжа II рода. Изложите последовательность действий при решении задач аналитической динамики с помощью уравнений Лагранжа II рода.
3N - число координат у N точек системы в пространстве. s - количество связей, нахоженных на систему. n=3N-s - число обобщ. координат определяющих положение системы (если связи голономные и удерживающие, то n - количество степеней свободы системы). 1) определить число степеней свободы механической системы и выбрать удобные обобщ. координаты; 2) вычислить Т системы в ее абсолютном движении и выразить эту энергию через обобщ. координаты и обобщ. скорости; 3) изобразить действующие на систему активные силы и силы трения, составить выражения для работы этих сил на возможном перемещ. и из этого выражения определить обобщ. силы соотв. выбранным обобщ. координатам; 4) вычислить производные, входящие в уравнения Лагранжа; 5) подставить все вычисленные величины в уравнения Лагранжа; 6) найти решения получившихся ДУ, соотв. заданным начальным условиям. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Если система в равновесии => любая точка системы в равновесии. Сумма активных сил
. Если система в равновесии => любая точка системы в равновесии. Сумма активных сил  и реакций связи
и реакций связи  , прилож. к каждой точке системы, должна быть равна нулю:
, прилож. к каждой точке системы, должна быть равна нулю:  ,
,  . Из этого следует, что и работа этих сил на любом возможном перемещении
. Из этого следует, что и работа этих сил на любом возможном перемещении  также равна нулю:
также равна нулю:  ,
,  .
.  в силу идеальности связей =>
в силу идеальности связей =>  равнодействующая сил
равнодействующая сил  ,
, 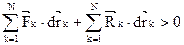 (2). В случае стационарных связей действ. перемещ. совпадают с одним из возможных, то есть
(2). В случае стационарных связей действ. перемещ. совпадают с одним из возможных, то есть  . Из (2) получим:
. Из (2) получим:  .
.  , что противоречит условию (1). *достаточность доказана*
, что противоречит условию (1). *достаточность доказана* , а радиус-вектор
, а радиус-вектор  , k-ой точки:
, k-ой точки:  . Возможное перемещ. каждой точки:
. Возможное перемещ. каждой точки:  (2). Подставим (2) в (1):
(2). Подставим (2) в (1):  , отсюда получим:
, отсюда получим:  (3). Вариации обобщ. координат
(3). Вариации обобщ. координат  независимы друг от друга => (3) выполнится, когда все обобщенные силы
независимы друг от друга => (3) выполнится, когда все обобщенные силы  равны нулю. Условие равновесия голономной системы в обобщ. коорд.:
равны нулю. Условие равновесия голономной системы в обобщ. коорд.:  .
. ,
,  . Умножим (1) скалярно на
. Умножим (1) скалярно на  .
. 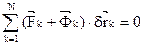 ;
; 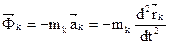 , и окончательно:
, и окончательно: 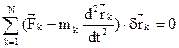
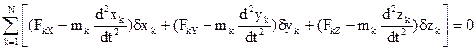
 , (
, (  )
)