
|
|
Рассмотреть решение задачи о падении тела в сопротивляющейся среде. Как определить критическую скорость падения.Тело массой m движется вниз без начальной скорости из начала координат О. Ось Ох вертикально вниз. На тело действует сила тяжести Дайте определение механической системы. Центр масс системы. Классификация сил действующих на систему. Запишите дифференциальные уравнения движения системы. Механической системой материальных точек, или просто системой, в механике называется совокупность взаимодействующих между собой материальных точек.
Центр масс системы - это такая точка, относительно которой статический момент массы равен нулю: Силы: заданные силы (выражения которых в зависимости от t, скоростей и координат точек известны) и реакции связи (не известные до исследования системы). С другой стороны: внешние (силы взаимод. между точками системы и точками, не принадлеж. системе) и внутренние (силы взаимод. между точками, принадлеж. данной системе).
Дать определение моментов инерции. Доказать связь между полярным и осевыми моментами инерции. Что такое радиус инерции. Какая ось называется главной центральной осью тела. - Полярным моментом инерции - Осевым моментом инерции материальной точки М относительно оси Оl называется произведение массы точки m на квадрат расстояние h до оси Оl: - Моменты инерции материальной точки относительно декартовых осей: Перепишем: Сложим, левые и правые части (1): - Точка находиться в плоскости xOy, моменты инерции материальной точки относительно осей х и y равны: - Момент инерции тела относительно оси Оl: - Если оба центробежных момента инерции, содерж. в индексах значок некоторой коорд. оси равны нулю, то эта ось - главная осью инерции тела. Например: Доказать формулы для вычисления моментов инерции прямолинейного тонкого стержня и прямоугольной пластины.
Стержень массой М - материальный прямолинейный отрезок АВ длиной l. Вычислим момент инерции этого стержня относительно оси Аy Тогда:
Линейная плотность стержня: Момент инерции стержня относительно центра масс С вычисляется аналогично. Пределы в этом случае надо брать от
ПРЯМОУГОЛЬНИК
Момент инерции всего прямоугольника: Аналогично относительно оси х:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
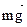 , напр. вниз, и сила сопротивления
, напр. вниз, и сила сопротивления 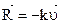 , напр. вверх, тогда ДУ движения тела:
, напр. вверх, тогда ДУ движения тела:  . Начальные условия при t = 0:
. Начальные условия при t = 0: 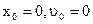 . Разделяем переменные:
. Разделяем переменные:  . Интегрир:
. Интегрир: 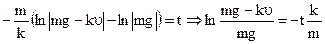
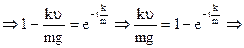
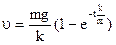 - закон изменения скорости. При
- закон изменения скорости. При  ,
,  . По истечении t движение становиться равномерным, то есть,
. По истечении t движение становиться равномерным, то есть,  к постоянной величине:
к постоянной величине:  .
. Центром масс механической системы называется геометрическая точка С, положение которой относительно выбранной системы координат определяется радиус-вектором
Центром масс механической системы называется геометрическая точка С, положение которой относительно выбранной системы координат определяется радиус-вектором 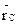 .
.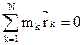 .
. (k = 1, 2, ..., N) система N таких уравнений называется ДУ движения механической системы в векторной форме. Если спроецировать уравнения на оси координат, то получим 3N ДУ.
(k = 1, 2, ..., N) система N таких уравнений называется ДУ движения механической системы в векторной форме. Если спроецировать уравнения на оси координат, то получим 3N ДУ.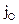 материальной точки М называется произведение массы m этой точки на квадрат расстояния r до точки О (полюса):
материальной точки М называется произведение массы m этой точки на квадрат расстояния r до точки О (полюса): 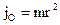 .
.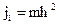 .
. .
.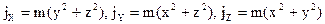 (1). Момент инерции точки относительно начала координат равен:
(1). Момент инерции точки относительно начала координат равен: 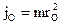 , перепишем:
, перепишем: 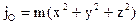 (2).
(2).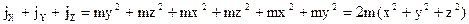 . С учётом (2):
. С учётом (2):  .
. . Перепишем:
. Перепишем: 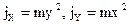 (3). Момент инерции точки относительно начала координат равен:
(3). Момент инерции точки относительно начала координат равен:  (4). Сложим, левые и правые части (3):
(4). Сложим, левые и правые части (3): 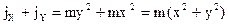 . С учётом (4):
. С учётом (4):  .
. .
.  - радиус инерции тела относительно данной оси:
- радиус инерции тела относительно данной оси: 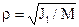 . Радиус инерции - расстояние от оси до точки, в которой нужно сосредоточить всю m тела, чтобы момент инерции массы был равен моменту инерции тела относительно данной оси.
. Радиус инерции - расстояние от оси до точки, в которой нужно сосредоточить всю m тела, чтобы момент инерции массы был равен моменту инерции тела относительно данной оси. , то z - главная ось инерции. Если эта ось проходит через центр масс тела, то она называется главной центральной осью инерции.
, то z - главная ось инерции. Если эта ось проходит через центр масс тела, то она называется главной центральной осью инерции.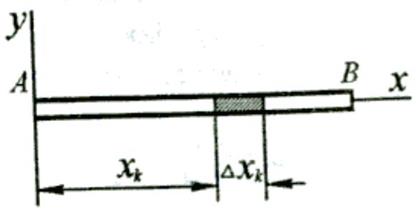 СТЕРЖЕНЬ
СТЕРЖЕНЬ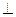 АВ. Разобьем стержень на бесконечно малые отрезки
АВ. Разобьем стержень на бесконечно малые отрезки  . Расстояние от
. Расстояние от 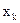 , а его массу -
, а его массу - 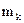 .
.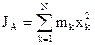 .
.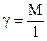 (кг/м). Масса
(кг/м). Масса 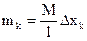 . Стержень однородный, тогда:
. Стержень однородный, тогда: 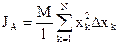 . Предел этой суммы - определённый интеграл по х в пределах от 0 до l:
. Предел этой суммы - определённый интеграл по х в пределах от 0 до l:  .
. . В результате:
. В результате:  .
.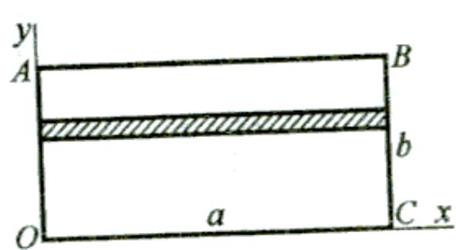 Тонкая однородная пластина ОАВС со сторонами а и b и массой М. Вычислим момент инерции относительно оси y (стороны ОА). Разобьем площадь ОАВС прямыми, параллельными оси х, на бесконечно узкие полоски. Масса полоски -
Тонкая однородная пластина ОАВС со сторонами а и b и массой М. Вычислим момент инерции относительно оси y (стороны ОА). Разобьем площадь ОАВС прямыми, параллельными оси х, на бесконечно узкие полоски. Масса полоски -  .
.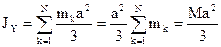 .
.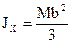 . Для момента инерции ОАВС относительно вершины О на основании связи полярного и осевых моментов, имеем:
. Для момента инерции ОАВС относительно вершины О на основании связи полярного и осевых моментов, имеем:  .
.