Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от координаты точки.
Сформулируйте математическую постановку и изложите решение двух основных задач динамики точки.
Первая: Зная закон движения материальной точки массы m, найти равнодействующую всех сил  , действующих на точку в каждый данный момент. , действующих на точку в каждый данный момент.
Движение точки задано координатным способом, т.е.  (1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат: (1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:  . Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы . Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы  , мы будем знать ее модуль и направление в каждый момент времени t. , мы будем знать ее модуль и направление в каждый момент времени t.
Вторая: По заданной силе  , действующей на материальную точку массы m, требуется определить закон движения точки. Сила , действующей на материальную точку массы m, требуется определить закон движения точки. Сила  и ее проекции могут зависеть от координат, скорости и времени. Запишем ДУ движения точки: и ее проекции могут зависеть от координат, скорости и времени. Запишем ДУ движения точки:

Решение сводиться к интегрированию системы трех ДУ второго порядка. Общее решение этой системы будет содержать 6 произвольных постоянных:
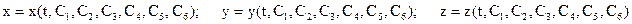
Константы найдём из начальных условий:  при при  . .
Вывести закон движения материальной точки, брошенной под углом к горизонту.
Материальная точка М массой m, брошена с поверхности под углом  к горизонту с начальной скоростью к горизонту с начальной скоростью  . Начальные условия (t = 0): . Начальные условия (t = 0):  (1). (1).
Единственной силой, является сила тяжести:  , направленная вниз. Проекции этой силы на оси координат: , направленная вниз. Проекции этой силы на оси координат:  . ДУ движения точки: . ДУ движения точки:  . .
Проинтегрируем ДУ движения точки:  (2) (2)
Интегрируем еще раз:  (3). (3).
Для определения постоянных  воспользуемся начальными условиями. воспользуемся начальными условиями.
Поставим начальные условия в (2) и в (3): 
Подставим постоянные в (3):  - закон движения точки. - закон движения точки.
Доказать необходимое и достаточное условия прямолинейного движения материальной точки и записать дифференциальное уравнение её прямолинейного движения.
ДУ свободной материальной точки в проекциях на декартовы оси координат:
 (1) (1)
Точка движется по прямой (ось Ох). Уравнения прямолинейной траектории точки: y = 0, z = 0 (2), следовательно, на основании (1):  (3). Равенства (3) означают, что если точка движется прямолинейно, то равнодействующая сил имеет постоянное направление и совпадающее с прямой, вдоль которой движется точка, то есть в осью Ох. Необходимое условие (3) не является достаточным. При условиях (3) уравнения (1) примут вид: (3). Равенства (3) означают, что если точка движется прямолинейно, то равнодействующая сил имеет постоянное направление и совпадающее с прямой, вдоль которой движется точка, то есть в осью Ох. Необходимое условие (3) не является достаточным. При условиях (3) уравнения (1) примут вид:  . Интегрируем: . Интегрируем:  . Ещё раз: . Ещё раз:  (4). Для опр. постоянных, восп. нач. усл. (t = 0): (4). Для опр. постоянных, восп. нач. усл. (t = 0):  . Постоянные: . Постоянные:  . Подставим постоянные в (4): . Подставим постоянные в (4):  (5). Из (5) видно, что траектория движения точки будет прямой, когда: (5). Из (5) видно, что траектория движения точки будет прямой, когда:  (6). Из равенств (3) и (6) следует, что свободная точка движется по прямой траектории, когда сила, приложенная к точке, имеет постоянное направление и начальная скорость точки параллельная этому направлению. (6). Из равенств (3) и (6) следует, что свободная точка движется по прямой траектории, когда сила, приложенная к точке, имеет постоянное направление и начальная скорость точки параллельная этому направлению.
 - ДУ прямолинейного движения свободной материальной точки. - ДУ прямолинейного движения свободной материальной точки.
Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от времени.
Мат. точка массой m движется вдоль оси Ох под действием  . ДУ прямолинейного движения: . ДУ прямолинейного движения: 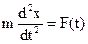 или или  , где , где  - проекция - проекция  на ось Ох. на ось Ох.
Разделяем переменные и интегрируем:  . Получим: . Получим: 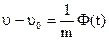 . Далее заменяя . Далее заменяя  , получаем: , получаем:  . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем:  . Получим: . Получим:  . Преобразуем: . Преобразуем:  - закон прямолин. движения точки. - закон прямолин. движения точки.
Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от скорости.
- Мат. точка массой m движется вдоль оси Ох под действием  . ДУ прямолин. движения: . ДУ прямолин. движения:  или или  , где , где  - проекция - проекция  на ось Ох. на ось Ох.
Разделяем переменные и интегрируем:  . Получим: . Получим: 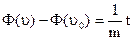 . Выразим . Выразим  , как функцию t: , как функцию t:  . Заменяя . Заменяя  , получаем: , получаем:  . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем:  . Получим: . Получим:  . Преобразуем: . Преобразуем:  - закон прямолинейного движения точки. - закон прямолинейного движения точки.
- Если после интегрирования  нельзя выразить как функцию t, то вводят замену: нельзя выразить как функцию t, то вводят замену:  . ДУ прямолинейного движения: . ДУ прямолинейного движения: 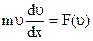 . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем:  . Получим: . Получим:  . Выразим . Выразим  , как функцию х: , как функцию х:  . Заменяя . Заменяя  , получаем: , получаем:  . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем:  . Получим: . Получим:  . Выразим х, как функцию t: . Выразим х, как функцию t:  - закон прямолинейного движения точки. - закон прямолинейного движения точки.
Изложить последовательность интегрирования дифференциального уравнения прямолинейного движения точки в случае, когда сила зависит только от координаты точки.
Мат. точка массой m движется вдоль оси Ох под действием  . ДУ прямолинейного движения: . ДУ прямолинейного движения:  или или  , где , где  - проекция - проекция  на ось Ох. на ось Ох.
Исключаем t:  . Получим: . Получим:  . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем:  . Получим: . Получим:  . Выразим . Выразим  , как функцию х: , как функцию х:  . Заменяя . Заменяя  , получаем: , получаем:  . Разделяем переменные и интегрируем: . Разделяем переменные и интегрируем:  . Получим: . Получим:  . Выразим х, как функцию t: . Выразим х, как функцию t:  - закон прямолинейного движения точки. - закон прямолинейного движения точки.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , действующих на точку в каждый данный момент.
, действующих на точку в каждый данный момент. (1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:
(1). Определив проекции ускорения из уравнений (1), запишем ДУ движения точки в проекциях на декартовы оси координат:  . Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы
. Решение сводиться к двукратному дифференцированию закона движения точки. Определив три проекции силы 
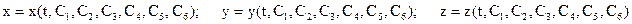
 при
при  .
. к горизонту с начальной скоростью
к горизонту с начальной скоростью  . Начальные условия (t = 0):
. Начальные условия (t = 0):  (1).
(1). , направленная вниз. Проекции этой силы на оси координат:
, направленная вниз. Проекции этой силы на оси координат:  . ДУ движения точки:
. ДУ движения точки:  .
. (2)
(2) (3).
(3). воспользуемся начальными условиями.
воспользуемся начальными условиями.
 - закон движения точки.
- закон движения точки. (3). Равенства (3) означают, что если точка движется прямолинейно, то равнодействующая сил имеет постоянное направление и совпадающее с прямой, вдоль которой движется точка, то есть в осью Ох. Необходимое условие (3) не является достаточным. При условиях (3) уравнения (1) примут вид:
(3). Равенства (3) означают, что если точка движется прямолинейно, то равнодействующая сил имеет постоянное направление и совпадающее с прямой, вдоль которой движется точка, то есть в осью Ох. Необходимое условие (3) не является достаточным. При условиях (3) уравнения (1) примут вид:  . Интегрируем:
. Интегрируем:  . Ещё раз:
. Ещё раз:  (4). Для опр. постоянных, восп. нач. усл. (t = 0):
(4). Для опр. постоянных, восп. нач. усл. (t = 0):  . Постоянные:
. Постоянные:  . Подставим постоянные в (4):
. Подставим постоянные в (4):  (5). Из (5) видно, что траектория движения точки будет прямой, когда:
(5). Из (5) видно, что траектория движения точки будет прямой, когда:  (6). Из равенств (3) и (6) следует, что свободная точка движется по прямой траектории, когда сила, приложенная к точке, имеет постоянное направление и начальная скорость точки параллельная этому направлению.
(6). Из равенств (3) и (6) следует, что свободная точка движется по прямой траектории, когда сила, приложенная к точке, имеет постоянное направление и начальная скорость точки параллельная этому направлению. - ДУ прямолинейного движения свободной материальной точки.
- ДУ прямолинейного движения свободной материальной точки. . ДУ прямолинейного движения:
. ДУ прямолинейного движения: 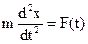 или
или  , где
, где  - проекция
- проекция  на ось Ох.
на ось Ох. . Получим:
. Получим: 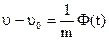 . Далее заменяя
. Далее заменяя  , получаем:
, получаем:  . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:  . Получим:
. Получим:  . Преобразуем:
. Преобразуем:  - закон прямолин. движения точки.
- закон прямолин. движения точки. . ДУ прямолин. движения:
. ДУ прямолин. движения:  или
или  , где
, где  . Получим:
. Получим: 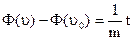 . Выразим
. Выразим  . Заменяя
. Заменяя  . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:  . Получим:
. Получим:  . Преобразуем:
. Преобразуем:  - закон прямолинейного движения точки.
- закон прямолинейного движения точки. . ДУ прямолинейного движения:
. ДУ прямолинейного движения: 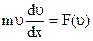 . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:  . Получим:
. Получим:  . Выразим
. Выразим  . Заменяя
. Заменяя  . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:  . Получим:
. Получим:  . Выразим х, как функцию t:
. Выразим х, как функцию t:  - закон прямолинейного движения точки.
- закон прямолинейного движения точки. . ДУ прямолинейного движения:
. ДУ прямолинейного движения:  или
или  , где
, где  . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:  . Получим:
. Получим:  . Выразим
. Выразим  . Заменяя
. Заменяя  - закон прямолинейного движения точки.
- закон прямолинейного движения точки.