
|
|
Введение в аналитическую механику. Понятие о числе степеней свободы. Уравнения связей.Числом степеней свободы ps называется число независимых перемещений, которые может совершать исследуемый объект. Например, у свободной материальной точки число степеней свободы равно трем Из-за наличия связей, ограничивающих перемещение исследуемого объекта, материальные точки, входящие в него, могут двигаться только по вполне определенным кривым в пространстве. Так, если движение материальной точки ограничено невесомым стержнем, то она может двигаться только по окружности, радиус которой равен длине стержня. Уравнения кривых, по которым вынуждены двигаться материальные точки, называются уравнениями связей. Эти уравнения могут иметь вид:
Здесь: k-индекс материальной точки;i-индекс вида связи. Если механическая система состоит только из материальных точек, то число степеней свободы этой системы можно определить как разность между общим числом степеней свободы материальных точек, предполагая их свободными, и числом уравнений связей, то есть
Для определения числа степеней свободы механических систем, состоящих из тел (механизмов и машин), существуют специальные методы, которые предлагаются в теории механизмов и машин. Однако в любом случае число степеней свободы механической системы равно числу дополнительных связей, которые надо наложить на механическую систему, чтобы она потеряла способность двигаться.
30.Понятие о возможных перемещениях, обобщенных координатах, вариациях обобщенных координат. Возможными перемещениями материальных точек называются воображаемые, бесконечно малые перемещения этих точек, допускаемые связями. В отличие от действительных перемещений Независимые переменные, с помощью которых можно однозначно определить состояние (координаты, скорость, ускорение) механической системы, называются обобщенными координатами. Они могут быть линейными, т.е. измеряться в единицах длины, и угловыми, измеряемыми как правило в радианах. Обобщенные координаты обозначаются Воображаемые бесконечно малые изменения обобщенных координат, допускаемые связями, называются вариациями обобщенных координат.
1) 2) 3) 4) 5) Число степеней свободы такого механизма по формуле (1):
Координаты, определяющие положение материальных точек механической системы, всегда можно представить в виде зависимости от обобщенных координат. Поэтому и уравнения связей, в которые входят координаты материальных точек, также могут быть представлены в виде функций только от обобщенных координат и времени. За обобщенную координату для кривошипно-шатунного механизма можно принять одну угловую переменную 1) 2) 3) 4) 5) 6) Возможные перемещения точек механизма:
Причем полный набор возможных перемещений для одного варианта имеет вид Всегда можно выразить возможные перемещения через вариации обобщенных координат. Пусть положение к-ой материальной точки определяется с помощью радиус-вектора
Действительное изменение радиус-вектора
При решении практических задач зависимость возможных перемещений от вариаций обобщенных координат можно найти:1)с помощью уравнений связей, 2)из кинематических соображений, за исключением некоторых случаев,3)а также иногда из геометрических рассуждений. Для приведенного выше механизма использование уравнений связей дает следующие зависимости:
31. Классификация связей. Если в уравнении связи не присутствует явно время, то такая связь называется стационарной, а если оно присутствует, то- нестационарной. Пример стационарной связи: При этом материальная должна всегда находиться на окружности с постоянным радиусом и эта окружность не изменяет своего положения в пространстве. Если уравнение связи представляет собой строгое равенство, то такая связь называется удерживающей, а если неравенство, то - неудерживающей. Равенство (1) представляет собой уравнение удерживающей связи. Уравнение неудерживающей связи имеет вид
Этот вид связи (гибкая нить) позволяет находиться материальной точке на окружности радиусом Если уравнение связи можно проинтегрировать или оно содержит только координаты материальных точек, то такая связь называется голономной. Если уравнение связи представляет собой дифференциальное уравнение, аналитическое решение которого пока невозможно найти, то такая связь называется неголономной. Равенство (1) представляет собой уравнение голономной связи. Если работа реакции связи на любом перемещении равна нулю, то такая связь называется идеальной, а иначе - неидеальной. При наличии неидеальных связей их надо отбрасывать, заменив реакциями и эти реакции включать в число внешних сил. 32. Работа силы на возможном перемещении.
Правую часть этого выражения можно выразить несколькими способами, а именно, раскрыв скалярное произведение и учитывая, что
(здесь Если скалярное произведение (1) представить в аналитическом виде, то (3). Кроме этого длину элементарной дуги (4). Здесь t-тангенциальная ось, Если сила Если сила 33. Принцип возможных перемещений. Принцип возможных перемещений утверждает, что: «Для равновесия механической системы с удерживающими идеальными стационарными связями необходимо и достаточно, чтобы: 1) сумма элементарных работ всех активных сил, приложенных к системе, на ее любом возможном перемещении равнялась нулю, то есть ; (1) 2) В начальный момент времени скорости всех материальных точек системы были равны нулю ( Доказательство: Необходимость. Пусть механическая система находится в равновесии. Следовательно,
Так как связи идеальные, то . Это соответствует условию (1) теоремы, что и доказывает справедливость утверждения принципа возможных перемещений. Достаточность. Пусть выполняются условия (1) и (2), то есть
Докажем, что механическая система находится в равновесии. По определению идеальности связей Поэтому Так как по основному закону динамики
Здесь С учетом этого Принцип возможных перемещений справедлив и при движении материальных точек и тел механической системы с постоянными скоростями. Примечание. Направление возможных перемещений определяется направлением скоростей, которые могли бы иметь точки и тела при их движении.
Пример №1. Необходимо определить модуль момента М пары сил, который необходимо приложить к шкиву «3» для равномерного подъема груза 1весом 900 Н. радиусы шкивов: Решение: Эта механическая система имеет число степеней свободы Тогда Вариация обобщенной координаты Так как
Принцип возможных перемещений для этой механической системы имеет вид:
Знаки работ определены, исходя из направлений силовых воздействий и возможных перемещений. Из равенства (1) имеем Пример 2.
Домкрат, изображенный на рисунке имеет размеры АО=ОВ=СЕ=ЕD=l, СВ=АD=2l. Определить необходимый шаг винта (h), если усилия приложенные к рукоятке Р=80 Н, а масса поднимаемого груза m=1000 кг. Расстояние от рукоятки до оси винта равно 20 см. Стержни AD, BC соединены шарнирно посередине. Решение. Механическая система находится в равновесии, поэтому можно применить принцип возможных перемещений для решения поставленной задачи. Число степеней свободы Рs=1. Обобщенная координата q=α. Зависимости возможных перемещений от вариации обобщенной координаты найдем с помощью уравнений связи:
Возможные перемещения:
Зависимость между перемещениями
Принцип возможных перемещений для данной задачи имеет вид:
Здесь Тогда отсюда При
34. Принцип возможных перемещений в обобщенных координатах. Понятие об обобщенной силе. Принцип возможных перемещений в обычном виде представляется формулой
Ранее было доказано, что возможное перемещение
Если подставить выражение (2) в формулу (1), то
Изменив порядок суммирования, получим
Здесь обобщенная сила
Если обобщенная координата имеет размерность длины, то обобщенная сила имеет размерность силы. Если обобщенная координата угловая, то обобщенная сила имеет размерность момента силы. Принцип возможных размещений в обобщенных координатах утверждает, что для равновесия механической системы необходимо и достаточно, чтобы обобщенные силы, соответствующие всем обобщенным координатам были равны нулю, то есть Доказательство. Принцип возможных перемещений
Это возможно при линейной независимости обобщенных координат только в случае, если Методы определения обобщенных сил. Существуют два довольно простых метода определения обобщенных сил. Первый метод можно применять для любых сил, а второй – только для консервативных. Первый метод состоит из выполнения следующих действий: Предполагаются постоянными все обобщенные координаты за исключением той координаты, для которой необходимо найти обобщенную силу, т. е.
Задают вариацию Находят зависимости возможных перемещений от одной вариации
Находят чему равна сумма работ активных сил на возможных перемещениях их точек приложения
Так как все вариации
Для всех Второй метод определения обобщенных сил можно применять только для консервативных сил В этом случае В этом случае полный дифференциал этой функции
Тогда
Сравнивая левую и правую части этого выражения, получим
Для всех Здесь П – потенциальная энергия (П=U). Пример.
Определить условия, при которых механическая система, изображенная на рисунке, находится в равновесии, если: блоки 4, 5, 6 и трос, связывающий грузы и блоки невесомые; наклонные поверхности гладкие; известны радиусы блоков r5=r, r6=R и углы α, β; блоки 5 и 6 не связаны между собой. Решение. Так как требуется установить условие равновесия этой механической системы, необходимо применить принцип возможных перемещений в обобщенных координатах. Число степеней свободы в данной механической системе ps=2. Следовательно необходимы две обобщенные координаты q1 и q2, определяющие положение грузов «1» и «2». Положение груза «3» однозначно определяется положением центра (т. О1) блока «4» с помощью координаты «y», которая зависит от обобщенных координат q1 и q2. Эту зависимость можно установить с помощью уравнения связи. Одной из связей этой механической системы является гибкая нерастяжимая нить, длина которой
Здесь b – длина нити на перегибах является постоянной величиной. Из этого равенства очевидно, что
Чтобы выяснить математический смысл обобщенных сил применим принцип возможных перемещений в обычном виде. Так как число степеней свободы ps=2, можем задать два независимых возможных перемещения, за которые возьмем
Принцип возможных перемещений
Здесь Принцип возможных перемещений в обобщенных координатах утверждает, что для равновесия данной механической системы необходимо и достаточно, чтобы обобщенные силы Q1=0 и Q2=0. Теперь эти обобщенные силы найдем с помощью первого метода. Чтобы найти Q1 выполним следующие условия: потребуем, чтобы зададим возможные перемещения грузу «1» -
С учетом того, сто в данном случае соотношение между скоростями точно такие же, как соотношения между перемещениями получим
определим сумму работ всех активных сил G1, G2, G3 на возможных перемещениях точек их приложения
определим обобщенную силу Q1 по формуле
Рассуждая аналогично изложенному выше, найдем что
что совпадает с полученным ранее результатом. Условия равновесия Q1=0 и Q2=0 в данном случае имеют вид:
Силы
Силовая функция равна работе сил поля при перемещении механической системы из начального положения q10, q20 =0, показанного пунктирной линией, в конечное, т. е.
Поэтому
тогда что так же совпадает с полученным ранее результатом. 35. Общее уравнение динамики. Общее уравнение динамики позволяет получать дифференциальные уравнения движения механической системы. Это уравнение получено последовательным применением принципа Даламбера и принципа возможных перемещений. Для механической системы принцип Даламбера можно представить следующим равенством
Здесь Если умножить скалярно все равенства (1) на возможное перемещение
Для голономных стационарных удерживающих связей
Здесь Равенство (3) получило название общего уравнения механики. Оно утверждает, что «сумма работ активных сил и сил инерции на возможном перемещении точек их приложения равна нулю». При решении задач равенство (3) можно представить в виде следующих формул:
Общее уравнение механики можно дописать так же для обобщенных координат. Для этого в выражение (4) надо подставить
Здесь
Тогда равенство (6) принимает вид
Из-за линейной независимости вариаций обобщенных координат нулю должно быть равно выражение в скобках, т. е. Итак, в обобщенных координатах общее уравнение динамики утвердает, что «сумма обобщенных сил активных сил и сил инерции должна быть равна нулю для всех Пример 1.
Дано: m1=3m, m2=m, m3=m, Решение. Эта механическая система имеет одну степень свободы. За обобщенную координату примем переменную, определяющую положение груза 1 – S1. Ускорения груза 1 «a1» и центра масс тела 3 «aC3» определим с помощью общего уравнения механики.
Чтобы составить его последовательно применим сначала принцип Даламбера, а затем принцип возможных перемещений, задав возможное перемещение грузу «1». В соответствии с принципом Даламбера: к телу «1», которое двигается поступательно, приложим только главный вектор сил инерции
К телу «2», которое совершает вращательное движение вокруг главной центральной оси инерции, приложим только главный момент сил инерции Теперь зададим возможное перемещение механической системы. Направление возможного перемещения тела «1» -
Из этих соотношений следуют зависимости между возможными перемещениями:
Дифференцируя выражение (2), найдем зависимости между ускорениями, которые необходимы для определения главных векторов и главных моментов сил инерции.
Поэтому
Тело «2» вращается вокруг главной центральной оси инерции и известен радиус инерции
Тело «3» двигается плоскопараллельно и представляет собой однородный диск. Поэтому
С учетом найденных моментов инерции
Главные векторы активные силы реакции связей Сумма работ активных сил на возможных перемещениях их точек приложения
Здесь
Работа реакций связей на возможных перемещениях их точек приложения
Тогда работа активных сил на возможных перемещениях их точек приложения
Сумма работ сил инерции на возможных перемещениях их точек приложения
Здесь:
Тогда сумма работ сил инерции на возможных перемещениях их точек приложений
Подставляя найденные суммы работ (3) и (4) в общее уравнение механики (1), получим
Откуда найдем 36. Уравнение Лагранжа II-го рода. Уравнение Лагранжа II-го рода рационально применять дифференциальные уравнения движения механической системы. Преимуществом этих уравнений является то, что число дифференциальных уравнений, определяющих движение исследуемой механической системы равно числу степеней свободы этой системы и не зависит от количества материальных точек и тел, входящих в неё. Уравнения Лагранжа II-го рода имеют следующий вид
Здесь: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а для твердого тела, совершающего вращательное движение, число степеней свободы равно единице
, а для твердого тела, совершающего вращательное движение, число степеней свободы равно единице 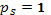 .
. ;
;  ;
;  .
.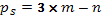 или
или  (1) при движении в плоскости
(1) при движении в плоскости возможные перемещения обозначаются символами
возможные перемещения обозначаются символами  .
. , при чем число обобщенных координат всегда равно числу степеней свободы, то есть
, при чем число обобщенных координат всегда равно числу степеней свободы, то есть  .
. Рассмотрим кривошипно-шатунный механизм, изображенный на рисунке. Здесь ОА=r, АВ= e. Будем предполагать, что данный механизм состоит из трех материальных точек О, А, В, связанных между собой невесомыми стержнями ОА, АВ. При этом перемещение всего механизма ограничено неподвижной шарнирной опорой в точке О и гладкой поверхностью, совпадающей с осью Оx. При таких связях их уравнения имеют вид:
Рассмотрим кривошипно-шатунный механизм, изображенный на рисунке. Здесь ОА=r, АВ= e. Будем предполагать, что данный механизм состоит из трех материальных точек О, А, В, связанных между собой невесомыми стержнями ОА, АВ. При этом перемещение всего механизма ограничено неподвижной шарнирной опорой в точке О и гладкой поверхностью, совпадающей с осью Оx. При таких связях их уравнения имеют вид: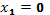 ;
; ;
; ;
;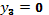 ;
; .
.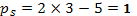 .
. , определяющую положение кривошипа, а следовательно и положение всего механизма. Тогда в уравнениях связей будет только одна переменная. Например, для рассматриваемого механизма:
, определяющую положение кривошипа, а следовательно и положение всего механизма. Тогда в уравнениях связей будет только одна переменная. Например, для рассматриваемого механизма: ;
;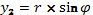 ;
; .
. или
или 
 ;
; 
 , а для другого варианта . При этом совершенно очевидно, что действительные перемещения принадлежат множеству возможных перемещений , то есть
, а для другого варианта . При этом совершенно очевидно, что действительные перемещения принадлежат множеству возможных перемещений , то есть  ,
,  ,
, 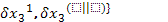 . Этому набору возможных перемещений соответствует набор вариаций обобщенной координаты .
. Этому набору возможных перемещений соответствует набор вариаций обобщенной координаты . , где
, где  , независящего явно от времени
, независящего явно от времени .
.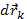 - это одно из возможных его изменений, то есть
- это одно из возможных его изменений, то есть  и по индукции
и по индукции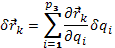 (2).
(2).
 (1).
(1). .
.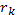 и внутри ее.
и внутри ее. Обозначим работу силы
Обозначим работу силы 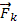 на ее возможном перемещении
на ее возможном перемещении  как δАк . Эту работу, по аналогии с элементарной работой силы на действительном перемещении -
как δАк . Эту работу, по аналогии с элементарной работой силы на действительном перемещении - 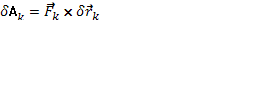 (1).
(1). , получим:
, получим: (2).
(2). - длина траектории, по которой может двигаться точка приложения силы)
- длина траектории, по которой может двигаться точка приложения силы) . С учетом этого элементарная работа силы на возможном перемещении:
. С учетом этого элементарная работа силы на возможном перемещении: , СМ=ρ.
, СМ=ρ. )».
)». для всех
для всех  . Здесь
. Здесь  реакции связей. Если задать механической системе возможное перемещение, то
реакции связей. Если задать механической системе возможное перемещение, то .
. , а следовательно выполняется условие, что
, а следовательно выполняется условие, что ;
;  .
.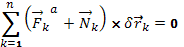 .
. , то можно записать, что
, то можно записать, что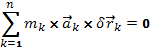 . (2)
. (2) , но
, но  , так как
, так как  (
(  ). С учетом этого
). С учетом этого  (
(  направлены по
направлены по 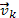 , следовательно – по
, следовательно – по  при отсутствии
при отсутствии 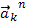 ), b – коэффициент пропорциональности.
), b – коэффициент пропорциональности.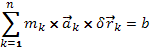
 будет иметь место, только в случае, когда
будет иметь место, только в случае, когда 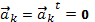 . Следовательно, выполняется условие равновесия механической системы
. Следовательно, выполняется условие равновесия механической системы  для всех
для всех 
 .
. =?. За обобщенную координату «ρ» возьмем угол поворота шкива «3» -
=?. За обобщенную координату «ρ» возьмем угол поворота шкива «3» - 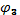 (
(  ).
).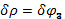 .
. показана на расчетной схеме. Зависимости возможных перемещений от вариации обобщенной координаты найдем из кинематических зависимостей.
показана на расчетной схеме. Зависимости возможных перемещений от вариации обобщенной координаты найдем из кинематических зависимостей. , то
, то  , откуда
, откуда  ,
, . Поэтому
. Поэтому 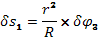 .
. или
или  (1)
(1) (Н×м).
(Н×м).
 ;
; 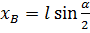 ;
;  .
.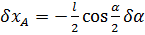 ;
;  ;
;  .
. и
и 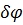 найдем из свойства винтовой передачи за один оборот винта (на угол 2π) гайка переместится на шаг (h) винта. Поэтому справедлива зависимость
найдем из свойства винтовой передачи за один оборот винта (на угол 2π) гайка переместится на шаг (h) винта. Поэтому справедлива зависимость 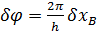 или
или
 .
.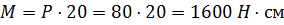 .
. ,
, .
.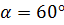 найдем
найдем .
. . (1)
. (1) может быть выражено в виде следующей зависимости от вариаций обобщенных координат
может быть выражено в виде следующей зависимости от вариаций обобщенных координат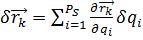 (2)
(2) .
. (3)
(3) или
или
 , для всех
, для всех  .
. т. е.
т. е.
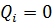 для всех
для всех  ,
,  ,
,
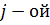 обобщенной координате
обобщенной координате  , полагая остальные вариации равными нулю (
, полагая остальные вариации равными нулю (  для всех
для всех 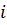 перечисленных выше).
перечисленных выше).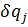 ,
,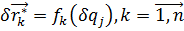
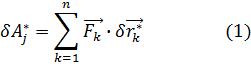
 , выраженная через обобщенные силы имеет вид
, выраженная через обобщенные силы имеет вид  , откуда
, откуда
 .
. .
. ,
,  ,
, 
 так же можно представить в виде функции обобщенных координат
так же можно представить в виде функции обобщенных координат  , где
, где 
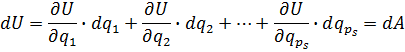





 . Возможное перемещение точки приложения силы тяжести
. Возможное перемещение точки приложения силы тяжести  груза «3» -
груза «3» -  выразим с помощью уравнения связи
выразим с помощью уравнения связи
 в данном случае записывается в следующем виде
в данном случае записывается в следующем виде


 имеют смысл множителей, стоящих при вариации обобщенных координат в выражении для принципа возможных перемещений.
имеют смысл множителей, стоящих при вариации обобщенных координат в выражении для принципа возможных перемещений. это равносильно прекращению движения груза «2». Тогда точка р1 становится мгновенным центром скоростей для блока «3»;
это равносильно прекращению движения груза «2». Тогда точка р1 становится мгновенным центром скоростей для блока «3»; и выразим возможное перемещение
и выразим возможное перемещение 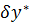 только через
только через 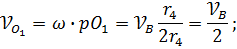
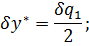

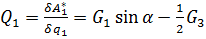 .
.

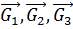 являются силами поля тяжести, т. е. они являются консервативными. Поэтому обобщенные силы можно определить и вторым способом, т. е. по формулам
являются силами поля тяжести, т. е. они являются консервативными. Поэтому обобщенные силы можно определить и вторым способом, т. е. по формулам

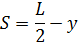
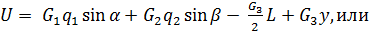

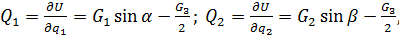
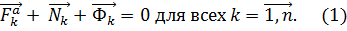
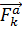 – активная сила,
– активная сила,  - реакция связи,
- реакция связи,  – сила инерции.
– сила инерции.
 С учетом этого равенство (2) приобретает вид
С учетом этого равенство (2) приобретает вид

 - работа активной силы на возможном перемещении ее точки приложения;
- работа активной силы на возможном перемещении ее точки приложения; 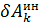 - работа силы инерции на возможном перемещении точки приложения этой силы.
- работа силы инерции на возможном перемещении точки приложения этой силы.


 и поменять порядок суммирования. В результате получим
и поменять порядок суммирования. В результате получим
 – обобщенная сила активных сил (эта обобщенная сила уже встречалась в принципе возможных переменных для обобщенных координат);
– обобщенная сила активных сил (эта обобщенная сила уже встречалась в принципе возможных переменных для обобщенных координат);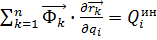 - обобщенная сила сил инерции.
- обобщенная сила сил инерции.
 для всех
для всех 

 r2=r=0,4 м, R3=2r,
r2=r=0,4 м, R3=2r,  f=0,1,
f=0,1,  =0,001 см, t=0,
=0,001 см, t=0, 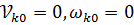 . Определить a1, aC3.
. Определить a1, aC3.
 . Ускорение
. Ускорение 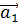 направим вниз по наклонной плоскости. Если окажется, что направление ускорения
направим вниз по наклонной плоскости. Если окажется, что направление ускорения  , направив его в сторону, противоположную угловому ускорению
, направив его в сторону, противоположную угловому ускорению  , направление которого должно соответствовать направлению ускорения груза 1
, направление которого должно соответствовать направлению ускорения груза 1  и главный момент сил инерции
и главный момент сил инерции  , направив его в сторону противоположную угловому ускорению
, направив его в сторону противоположную угловому ускорению  . Направления углового ускорения
. Направления углового ускорения 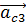 должны соответствовать направлению ускорения
должны соответствовать направлению ускорения  и
и  указывают, что эти векторы должны быть направлены в противоположную сторону соответствующих ускорений.
указывают, что эти векторы должны быть направлены в противоположную сторону соответствующих ускорений. возьмем в соответствие с направлением ускорения
возьмем в соответствие с направлением ускорения 
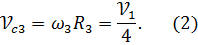



 , поэтому
, поэтому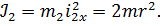

 главные моменты сил инерции определяются по формулам
главные моменты сил инерции определяются по формулам
 показаны на расчетной схеме. Противоположно соответствующим ускорениям
показаны на расчетной схеме. Противоположно соответствующим ускорениям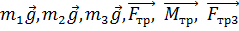 ,
, показаны на расчетной схеме.
показаны на расчетной схеме.
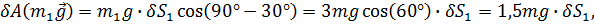
 так как точка С2 неподвижная,
так как точка С2 неподвижная,


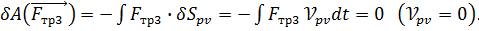
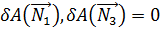 , т. к.
, т. к.  перпендикулярны соответствующим перемещениям.
перпендикулярны соответствующим перемещениям. , т. к. т. С2 неподвижная.
, т. к. т. С2 неподвижная.

 ,
, ,
,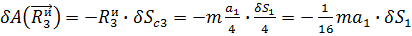 ,
, .
. . (4)
. (4)
 .
.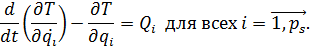
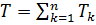 - кинетическая энергия механической системы;
- кинетическая энергия механической системы;  - обобщенная скорость;
- обобщенная скорость;  - обобщенная координата;
- обобщенная координата; 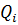 - обобщенная сила;
- обобщенная сила;  – частная производная от кинетической энергии механической системы по обобщенной скорости;
– частная производная от кинетической энергии механической системы по обобщенной скорости;  - частная производная от кинетической энергии механической системы по обобщенной координате;
- частная производная от кинетической энергии механической системы по обобщенной координате;  - полная производная по времени от выражения в скобках.
- полная производная по времени от выражения в скобках.