
|
|
Потенциальное силовое поле.Силовое поле- это область физического пространства, в каждой точке которой действуют силы, зависящие явно только от координат, определяющих положение исследуемого объекта и времени. Если силы поля явно от времени не зависят, то они называются консервативными, силовое поле, в котором действует только такие силы, называется силовым потенциальным полем. Дальше пойдет речь о таких полях, где проекция сил поля на оси декартовой системы координат не зависят явно от времени: Структуру силового поля можно выявить с помощью силовых линий, дифференциальные уравнения которых имеют вид:
Признаком существования силового поля является наличие такой функции
и выполнение требований, чтобы:
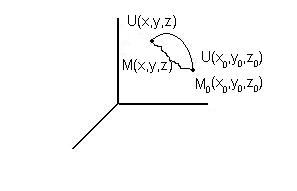
Действительно, если силовое поле существует, то существует и силовая функция Силовая функция потенциального силового поля является функцией нескольких переменных. Поэтому полный дифференциал этой функции, если она не зависит от времени явно, имеет вид или окончательно то есть дифференциал силовой функции равен элементарной работе силы тока. Равенство (2) может быть использовано для нахождения силовой функции с точностью до постоянного интегрирования, потому, что интегрируя равенство (2), получим
или окончательно 1. Если равенство (3) положить А=0, то получим уравнение поверхности, при перемещении исследуемого объекта по которой силы поля не будут совершать работу. Такие поверхности называются поверхностями уровня. 2. Если материальная точка движется в силовом потенциальном поле, то работа силы поля не зависит от траектории движения этой точки. 3. Если материальная точка движется в силовом потенциальном поле по замкнутой траектории и возвращается в первоначальное положение, то работа силы поля на таком перемещении этой точки равно нулю, то есть
4. Сила поля совершает работу только при переходе материальной точки с одной поверхности уровня на другую. 5. Сила поля всегда направлена по главной нормали к поверхности уровня, так как Здесь дифференциал 6. Сила поля всегда направлена в сторону возрастания силовой функции Так силовая функция определяется равенством
то есть силовую функцию можно определить как работу, выполненную силой поля, при перемещении исследуемого объекта из положения, где силовая функция принята равной нулю, в произвольное положение. Кроме силовой функции встречаются понятие потенциальной энергии, как работа силы поля при мысленном перемещении исследуемого объекта из произвольного положения в положение, где потенциальная энергия была принята нулю. Из этого определения следует, что потенциальная энергия П равна силовой функции с обратным знаком, то есть В качестве особого положения механической системы, где силовая функция U и потенциальная энергия “П” равны нулю, рационально принимать или начальное положение механической системы, или положение её устойчивого равновесия, если такое положение имеется. Под положением устойчивого равновесия механической системы следует понимать такое ее положение, в которое она возвращается под действием сил поля, после прекращения действия других сил или иных причин, из-за которых механическая система покинула это свое положение устойчивого равновесия. Примеры силовых потенциальных полей. 1. Поле силы тяжести Сила тяжести является частным случаем силы гравитации в условиях планеты Земля. Хотя сила тяжести имеет постоянную величину и направление (область действия силы тяжести не соответствует определению силового поля), все-таки можно говорить о поле силы тяжести, как о частном случае поля гравитации. Проекции силы тяжести на оси системы координат Декарта:
Поверхностями уровня будут z=const, то есть плоскости ”П” параллельные координатной плоскости xOy.
2. Поле центральной силы
Проекции центральной силы на координатные оси Тогда
Полагая 3. Поле силы гравитации Силу гравитации представим в следующем виде
С учетом этого Интегрируя выражение В данном случае поверхности уровня представляют собой сферы, центры которых совпадают с центром куда направлена сила гравитации (с началом отсчета системы координат).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
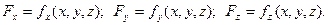
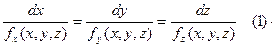
 , частные производные от которой по координатам будут равны проекциям сил на соответствующие оси, то есть
, частные производные от которой по координатам будут равны проекциям сил на соответствующие оси, то есть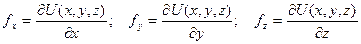
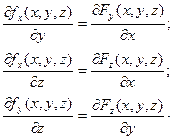
 и аналогично для остальных равенств.
и аналогично для остальных равенств.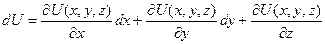
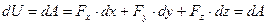 (2),
(2),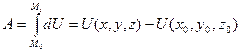
 (3).
(3).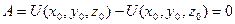
 (4)
(4) радиус-вектора
радиус-вектора  , определяющее положение материальной точки, которая перемещается по поверхности уровня, направлен всегда по касательной к этой поверхности. Равенство (4) выполняется, если
, определяющее положение материальной точки, которая перемещается по поверхности уровня, направлен всегда по касательной к этой поверхности. Равенство (4) выполняется, если 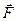 перпендикулярна дифференциалу
перпендикулярна дифференциалу  и А>0 (см. формулу 3), но
и А>0 (см. формулу 3), но  только в том случае, когда направление силы
только в том случае, когда направление силы 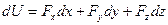 с точностью до постоянной интегрирования, то можно за счет выбора этой постоянной интегрирования всегда сделать так, чтобы в особом положении механической системы силовая функция
с точностью до постоянной интегрирования, то можно за счет выбора этой постоянной интегрирования всегда сделать так, чтобы в особом положении механической системы силовая функция  обратилась в нуль, то есть
обратилась в нуль, то есть  . Тогда получим, что
. Тогда получим, что ,
, .
. , поэтому
, поэтому  , откуда интегрируя, получим
, откуда интегрируя, получим  , где С- постоянная интегрирования.
, где С- постоянная интегрирования.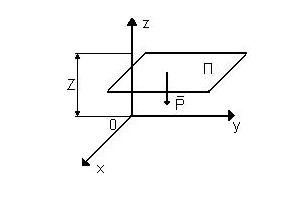
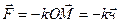 , где
, где  , x,y,z- координаты точки M, к- коэффициент пропорциональности.
, x,y,z- координаты точки M, к- коэффициент пропорциональности.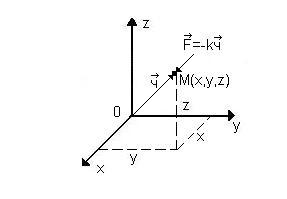
 .
. . Дифференциал от функции
. Дифференциал от функции 
 , следовательно
, следовательно  , откуда интегрируя, получаем:
, откуда интегрируя, получаем: и
и  .
. , получим уравнение поверхности уровня:
, получим уравнение поверхности уровня:  , то есть уравнение сферы, центр симметрии которой совпадает с началом отсчета координат (с центром, в которой направлена сила
, то есть уравнение сферы, центр симметрии которой совпадает с началом отсчета координат (с центром, в которой направлена сила  ).
). (см. работу силы гравитации). Её проекции на координатные оси равны:
(см. работу силы гравитации). Её проекции на координатные оси равны: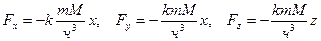 .
.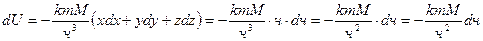 .
. , получим
, получим  .
.