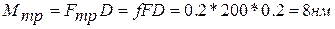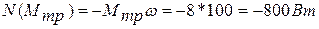|
|
Работы сил, вычисляемые непосредственно по заданным силам и перемещениям.1. Работа силы тяжести
Для вычисления ее работы используем формулу (3)
2. Работа центральной силы
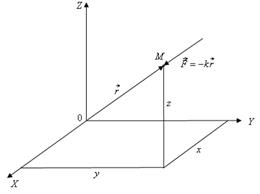
Рассмотрим случай, когда центр (т.О) куда направлена сила совпадает с началом отсчета радиус-вектора
Чтобы избавиться от символов векторных величин используем равенство Тогда элементарная работа силы Интегрируя получим Сила упругости
пружины (
3. Работа силы гравитации Величина силы гравитации определяется по формуле Проекции этой силы на оси координат Элементарная работа такой силы по формуле (3).
Интегрируя, получим Для постоянных сил и моментов пар сил формулы (6) и (8) принимают вид
Необходимо учитывать, что работа силы может быть: - больше нуля, если направление силы соответствует направлению перемещения, которое и указывается направлением скорости - меньше нуля, если направление силы не соответствует направлению перемещения; - равно нулю, если сила перпендикулярна к направлению перемещения Теорема о работе равнодействующей и главного вектора Равнодействующая
Теорема о работе равнодействующей и главного вектора утверждает, что: «Работа равнодействующей/главного вектора системы сил равна алгебраической сумме работ всех сил, входящих в эту систему.» Доказательство Умножив скалярно левые и правые части векторных равенств на дифференциал (
Работа и мощность произвольной системы сил, действующих на твердое тело Пусть на свободное твердое тело действует произвольная система сил
где Сначала найдем мощность одной k-ой силы
Здесь Окончательно имеем
Элементарная работа всех сил, действующих на твердое тело:
то есть элементарная работа всех сил, действующих на твердое тело, равна сумме элементарных работ главного вектора и проекции главного момента на мгновенную ось вращения (ρ). Мощность всех сил: Если тело двигается поступательно, то ω=0, dφ = ωdt = 0
Если тело вращается вокруг неподвижной оси, то выбрав за полюс т.О, лежащую на этой оси, получим: где φ-ось вращения тела. Интегрируя, найдем Если тело движется плоско-параллельно, то
Пример 1.
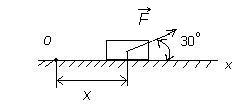
На тело действует сила F = 4x3 , которая направлена по отношению к оси Ох под постоянным углом α = 30о. Необходимо опредлить работу этой силы при перемещении тела из положения с координатой х0 = 0 в положение с координатой х1=1м.
Решение: Работа переменной силы:
Пример 2.
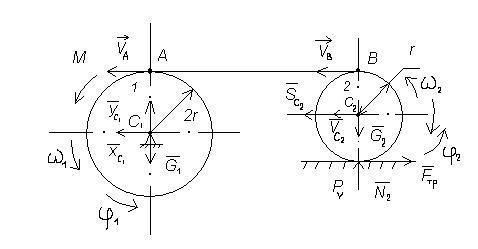
К барабану «1» приложена пара сил с постоянным моментом М = 10н.м. Цилиндр «2» массой m2 = 10 кг катится без скольжения по неподвижной шероховатой поверхности. Коэффициент трения качения δ = 0,01 м. Необходимо определить работу всех сил, действующих на эту механическую систему при повороте барабана «1» на N1 = 10 оборотов. Решение: Силы, действующие на данную механическую систему показаны на рисунке:
М – пара сил,
Направление перемещение указывается скоростями. Чтобы найти соотношения между перемещениями, найдем сначала соотношения между скоростями:
откуда ω2=ω1. Здесь Рv – мгновенный центр скоростей для тела «2», которое движется плоско-параллельно, РvВ – расстояние от мгновенного центра скоростей Рv до точки В. Скорость т.С2 : Соотношение между перемещениями точно такие же, как и между скоростями (за исключением случая колебаний). Это легко показать, например:
и интегрируя, получим Работа всех сил, действующих на механическую систему, равна сумме работ каждой из сил, то есть для данной механической системы:
Работы
Определим чему равна работа силы трения Fтр, приложенной в мгновенном центре скоростей.
(υPv=0 по определению мгновенного центра скоростей) Работа момента пары сил:
Момент трения: Работа от момента трения:
(ускорение земного притяжения g приняли равным 10м/с2) Таким образом:
Пример 3.
К диску диаметром D=0,2м, который вращается с угловой скоростью ω=100с-1, прижимаются две колодки с силой F=200Н. Необходимо определить мощность силы трения, если коэффициент трения скольжения тормозных колодок о диск f=0,2. Решение: Силы трения
Так как Мтр=const, мощность этого момента трения определим по формуле:
Знак минус появился из-за того, что Мтр направлен противоположно ω.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 .
.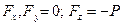
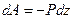
 , где
, где  может быть положительной и отрицательной, поэтому
может быть положительной и отрицательной, поэтому  .
. .
.
 . Тогда при
. Тогда при  по формуле (3) имеем
по формуле (3) имеем .
. и найдем дифференциалы левой и правой частей
и найдем дифференциалы левой и правой частей  или
или  , откуда
, откуда  .
.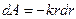
 .
. представляет собой частный случай центральной силы. Пусть она всегда будет направлена по оси X
представляет собой частный случай центральной силы. Пусть она всегда будет направлена по оси X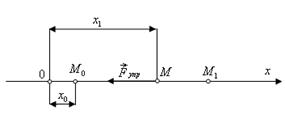
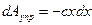
 . Если за начало отсчета принять точку (10), в которой
. Если за начало отсчета принять точку (10), в которой  и она совпадет с начальным положением материальной точки, то
и она совпадет с начальным положением материальной точки, то  и
и  - приобретает смысл полной деформации
- приобретает смысл полной деформации ). Тогда работа силы упругости может быть выражена формулой
). Тогда работа силы упругости может быть выражена формулой . Следует учесть, что x1 может оказаться x0 и тогда работа от силы упругости будет положительной.
. Следует учесть, что x1 может оказаться x0 и тогда работа от силы упругости будет положительной. . Здесь k – гравитационная постоянная; m1, m2 – массы тел; r – кратчайшее расстояние между телами. Принимая во внимание, что сила гравитации
. Здесь k – гравитационная постоянная; m1, m2 – массы тел; r – кратчайшее расстояние между телами. Принимая во внимание, что сила гравитации  направлена всегда противоположно радиус-вектору, запишем ее так
направлена всегда противоположно радиус-вектору, запишем ее так  .
. ;
;  ;
;  .
.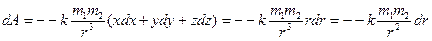
 .
. и
и  .
. ;
; и главный вектор
и главный вектор  системы сил определяются одинаково
системы сил определяются одинаково (1)
(1) ) радиус-вектора, определяющего положение точки приложения равнодействующей/центра приведения главного вектора, получим
) радиус-вектора, определяющего положение точки приложения равнодействующей/центра приведения главного вектора, получим или
или  , а интегрируя, получим
, а интегрируя, получим  . Аналогично для главного вектора
. Аналогично для главного вектора  .
. . Выберем в теле т.О за полюс. Тогда абсолютная скорость k-ой точки тела
. Выберем в теле т.О за полюс. Тогда абсолютная скорость k-ой точки тела ,
, - угловая скорость вращения тела вокруг мгновенной оси Р, проходящей через полюс т.О;
- угловая скорость вращения тела вокруг мгновенной оси Р, проходящей через полюс т.О;  - радиус-вектор определяющий положение k-ой силы.
- радиус-вектор определяющий положение k-ой силы. .
.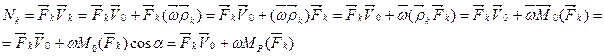
 - момент силы
- момент силы  относительно мгновенной оси Р.
относительно мгновенной оси Р. , откуда находим
, откуда находим  или
или .
.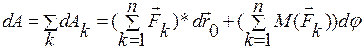 или
или , где
, где - главный вектор сил
- главный вектор сил - проекция главного момента сил системы на ось ρ, происходящей через полюс (центр приведения) т.О. Тогда:
- проекция главного момента сил системы на ось ρ, происходящей через полюс (центр приведения) т.О. Тогда: ,
, .
. ;
; 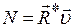
 и тогда
и тогда  и
и  ,
, , а при Мρ = const,
, а при Мρ = const, 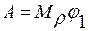
 ,
, .
.
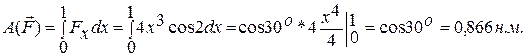
 силы тяжести тел «1» и «2»
силы тяжести тел «1» и «2» - момент трения качения, который должен быть направлен противоположно угловой скорости тела «2»,
- момент трения качения, который должен быть направлен противоположно угловой скорости тела «2», реакция неподвижной опоры,
реакция неподвижной опоры, - реакция поверхности, направленная по главной нормали к поверхности (N2=G2)
- реакция поверхности, направленная по главной нормали к поверхности (N2=G2) сила трения, причем Fтр=fтр качN2 не известна по величине.
сила трения, причем Fтр=fтр качN2 не известна по величине.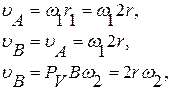
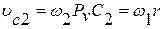
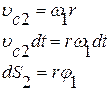
 , таким образом φ2=φ1 (т.к. ω2=ω1)
, таким образом φ2=φ1 (т.к. ω2=ω1)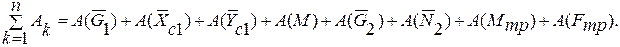
 , так как точка приложения этих сил неподвижная.
, так как точка приложения этих сил неподвижная. , так как перемещение точек приложения этих сил перпендикулярны силам.
, так как перемещение точек приложения этих сил перпендикулярны силам.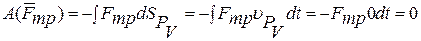
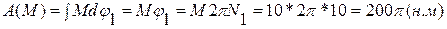
 .
.
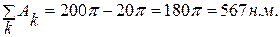
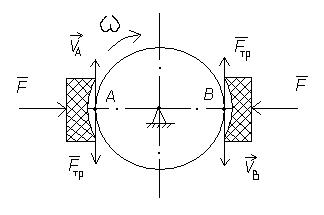
 между колодками и диком показаны на рисунке. Они направлены противоположно скоростям в точках их приложения и образуют пару сил с моментом:
между колодками и диком показаны на рисунке. Они направлены противоположно скоростям в точках их приложения и образуют пару сил с моментом: