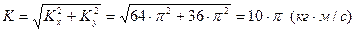|
|
СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ О ДВИЖЕНИИ ЦЕНТРА МАСС1. Если главный вектор внешних сил, действующих на механическую систему равен нулю
Если 2. Если проекция главного вектора внешних сил на какую – либо ось равна нулю, то в направлении этой оси центр масс механической системы или не двигается или двигается с постоянной скоростью
Если Пример 1. Дано: Центр масс колеса – С движется по окружности радиуса R=2м. Согласно закону
рис 7. Решение:Так как траектория движения центра масс колеса известны, то для определения главного вектора внешних сил рационально использовать теорему о движении центра масс в проекциях на оси естественной системы координат Тогда При t=1с Пример 2. Дана: Определите координату центра масс кривошинно - шатунного механизма в указанном положении на чертеже, если масс кривошинна ОА m1 = 8 кг, масса шатуна АВ m2 = 16кг, и масса ползуна «В» m3 = 4кг, длина шатуна
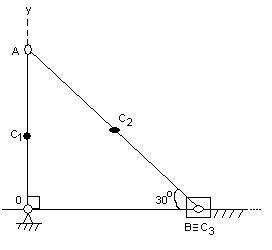
рис 8. Решение: Координату центра масс xc , этого механизма надо определять по формуле : Здесь масса механизма Координаты центров масс тел :
Тогда Пример 3. Дано: Тело 1 массой m1 = 4кг может двигаться по горизонтальной направляющей. На какое расстояние переместиться тело, когда однородный стержень 2 массой m2 = 2 кг и длиной L = 0,6м , опускаясь под действием сил тяжести займет вертикальное положение. В начальный момент данная механическая система находиться в покое.
рис 9. Решение: Покажем внешние силы Теорема о движении центра масс в проекции на ось Х в данном случае имеет вид:
Интегрируя дважды это дифференциальное уравнение, получим где Определим постоянные интегрирования по начальным условиям: Откуда С1 = 0 и При движении стержня 2 из горизонтального положения в вертикальное, вид теоремы о движении центра масс в проекции на ось Х (уравнение (1)) не изменяется. Следовательно, координата центра масс xc остается постоянной. Поэтому при перемещении центра масс стержня вниз и влево координата центра масс первого тела должна переместиться вправо. Новое положение механической системы также покажем на рисунке, причем Тогда 10. ПОНЯТИЕ О КОЛИЧЕСТВЕ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ Количество движения материальной точки это вектор направлений по вектору скорости и определяемый по формуле:
рис 10. Здесь Если материальная точка совершает сложные движения, то ее абсолютная скорость Тогда количество движений материальной точки :
то есть, оно равно векторной сумме количеств переносного Пример Дано: Для момента времени t1=1c необходимо определить количество движений тела 2 массой m2 = 1кг, если оно движеться по отношению к телу 1 согласно закону
рис 11. Решение: Тело 2 совершает сложное движение, которое состоит из переносного поступательного движения в направлении оси по закону xe(t) и относительного прямолинейного движения по закону Sr(t). Найдем переносную и относительную скорости: Причем Векторы количеств движения
Векторное равенство
Величину количества движения тела 2 найдем по теореме Пифагора:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , то центр масс этой системы или не двигается, или двигается прямолинейно с постоянной скоростью.
, то центр масс этой системы или не двигается, или двигается прямолинейно с постоянной скоростью.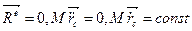
 , то
, то 
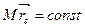
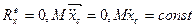
 , то
, то 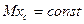
 .Определить при t = 1с модуль главного вектора внешних сил, приложенных к колесу, если его масса m = 20кг
.Определить при t = 1с модуль главного вектора внешних сил, приложенных к колесу, если его масса m = 20кг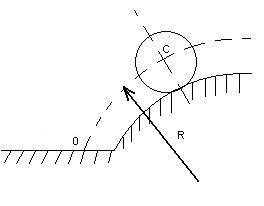


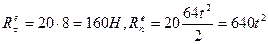
 , а
, а 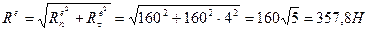
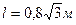
 .
.
 ,
,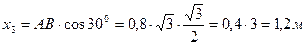
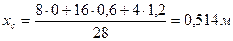
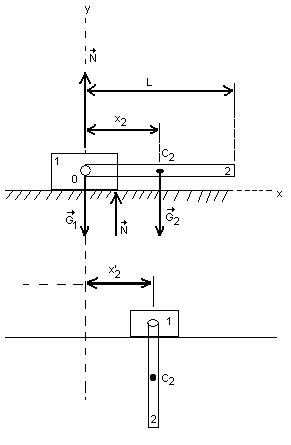
 , действующие на исследуемую механическую систему, которые должны быть изложены в центрах тяжести соответствующих тел и направлены вертикально, то есть перпендикулярно оси ОХ. Кроме этих активных сил на данную механическую систему действует еще реакция гладкой поверхности
, действующие на исследуемую механическую систему, которые должны быть изложены в центрах тяжести соответствующих тел и направлены вертикально, то есть перпендикулярно оси ОХ. Кроме этих активных сил на данную механическую систему действует еще реакция гладкой поверхности  , также перпендикулярная оси «х».
, также перпендикулярная оси «х». (1)
(1) ,
,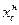 - начальное положение центра масс.
- начальное положение центра масс. .
.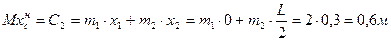
 , где S - перемещение груза 1.
, где S - перемещение груза 1. , приравняем начальное
, приравняем начальное  и конечное положение
и конечное положение  , получим равенство
, получим равенство  , откуда
, откуда 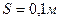
 (1)
(1)
 - скорость материальной точки по отношению к неподвижной системе отсчета, то есть это абсолютная скорость.
- скорость материальной точки по отношению к неподвижной системе отсчета, то есть это абсолютная скорость.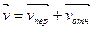
 (2)
(2) и относительного
и относительного  движений.
движений.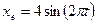

 , При
, При 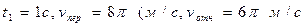
 направлена параллельно оси 0x, а
направлена параллельно оси 0x, а  по прямой ОА вверх.
по прямой ОА вверх. и
и  направлены по соответствующим скоростям. Величины этих векторов при t1=1c
направлены по соответствующим скоростям. Величины этих векторов при t1=1c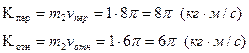
 можно спроектировать на координатные оси
можно спроектировать на координатные оси