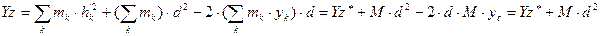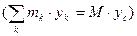|
|
СВОЙСТВА ГЛАВНЫХ ОСЕЙ ИНЕРЦИИПонятие о центре масс механической системы. Центр масс механической системы (т. С)– это геометрическая точка в пространстве, положение которой определяется по формулам:
Здесь
Следует отметить, что понятие центра масс механической системы является более общим, чем понятие центра тяжести, так как центр масс существует для любой механической системы, в то время как понятие центра тяжести может быть употреблено только в пределах планеты Земля. Также существенным различием является то, что центр масс механической системы может изменять свое положение по отношению к элементам системы, а центр тяжести не может изменять своего положения по отношению к отдельным частям тела. Однако следует помнить, что понятия центра тяжести и центра масс совпадают для твердого тела, если твердое тело рассматривать как неизменяемую механическую систему.
Инерционные параметры твердого тела и механической системы. При поступательном движении твердого тела мерой инерционных свойств является его масса. При поступательном движении твердого тела и при движении механической системы мерой их инерционных свойств являются также моменты инерции. Наиболее часто используются понятия момента инерции относительно полюса– полярный момент инерции (Jo), момента инерции относительно оси–осевой момент инерции (Jx , Jy , Jz) и центробежные моменты инерции (Jxy , Jxz , Jyz). Если механическая система представляет собой совокупность конечного числа взаимосвязанных материальных точек, то моменты инерции определяются по следующим формулам:
Здесь L–ось, относительно которой определяется момент инерции (может быть Для определения моментов инерции твердого тела используются следующие формулы:
Здесь
Моменты инерции относительно начала отсчета и осей декартовой системы координат.
Изобразим k–ую материальную точку в произвольном положении. Ее положение в пространстве определяется с помощью радиус–вектора ( Тогда полярный момент:
Осевой момент инерции Аналогично для других координатных осей
Если сложить осевые моменты инерции, то получим
Момент инерции относительно оси, проходящей в заданном направлении.
Здесь Момент инерции
но
Тогда
Используя формулу
Оси инерции x1,y1,z1, относительно которых центробежные моменты инерции ЭЛЛИПСОИД ИНЕРЦИИ Если взять какую- либо точку 0 на теле и ось OL, проходящую через эту точку 0, то можно определить момент инерции относительно этой оси – YOL. При изменении направления оси OL (cos
где
Это уравнение замкнутой поверхности второго порядка. Для главной центральной оси инерции x1y1z1 равенство (3) имеет вид
Если ввести обозначения СВОЙСТВА ГЛАВНЫХ ОСЕЙ ИНЕРЦИИ Теорема 1. Если механическая система ( твердое тело) имеет ось материальной симметрии, то эта ось является главной центрально осью инерции. Теорема 2. Если механическая система имеет относительно материальной симметрии, то любая ось, перпендикулярная к этой плоскости является главной (но не центральной) осью инерции. Теорема 3. Центральные моменты инерции, имеющие хотя бы один индекс главной оси инерции, равен нулю. Теорема 4. Для любой точки, лежащей на главной центральной оси инерции, главные оси инерции, параллельны соответствующим главным центральным осям инерции.
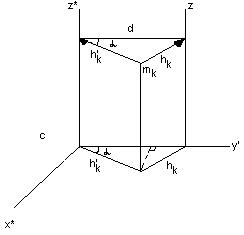
рис 1. Здесь Cx2, Cy1 2, Cz2 – главные центральные оси инерции. Главные оси инерции 0x1 || Cx1*, 0y1 || Cy1*, 0z1 || Cz* Теорема 5. (Теорема Шнейнера – Гюйгенса) Момент инерции Yz механической системы (твердого тела) относительно центральной оси, параллельной данной, и произведение массы – М механической системы на кратчайшие расстояния между осями «d» в квадрате Доказательство:
Рис 2. Пусть 0z – произвольная ось инерции, 0z* - центральной оси инерции.
здесь
Так как yc = 0 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (1)
, (1) (2)
(2) –радиус–векторы, определяющие соответственно положение центра масс механической системы (т. С) и положение материальных точек или центры тяжести k–ых тел механической системы;
–радиус–векторы, определяющие соответственно положение центра масс механической системы (т. С) и положение материальных точек или центры тяжести k–ых тел механической системы; –координаты, определяющие положение центра масс механической системы;
–координаты, определяющие положение центра масс механической системы; –координаты, определяющие положение материальных точек или центры тяжести тел механической системы;
–координаты, определяющие положение материальных точек или центры тяжести тел механической системы; –масса материальной точки или тела;
–масса материальной точки или тела; –масса всей механической системы
–масса всей механической системы 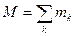 .
.
 ).
).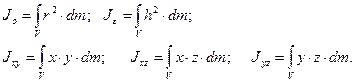
 – символ интегрирования по объему.
– символ интегрирования по объему.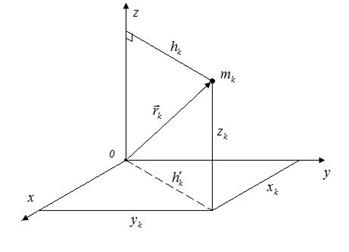
 ) и трех координат (
) и трех координат ( 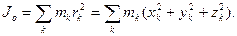

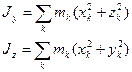
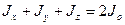 .
.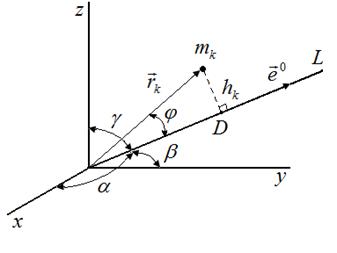
 – направляющие углы,
– направляющие углы, 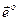 – орт оси
– орт оси 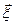
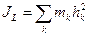 ,
, , где
, где 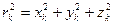
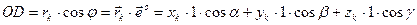
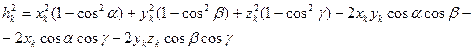
 , чтобы избавиться от выражений в скобках.
, чтобы избавиться от выражений в скобках. равны нулю, называются главными осями инерции. Если ось инерции проходит через центр масс механической системы (центр тяжести тела) , но она называется центральной осью инерции. Главная ось инерции, проходящая через центр масс, называется главной центральной осью инерции.
равны нулю, называются главными осями инерции. Если ось инерции проходит через центр масс механической системы (центр тяжести тела) , но она называется центральной осью инерции. Главная ось инерции, проходящая через центр масс, называется главной центральной осью инерции. , cos
, cos  , cos
, cos  в формуле (1)) будет изменяться момент инерции YOL=Y. Отложим на оси OL отрезок прямой OM= r =
в формуле (1)) будет изменяться момент инерции YOL=Y. Отложим на оси OL отрезок прямой OM= r =  . Построим систему координат 0x1y1z1 . Обозначим координаты точки М через x1y1z1 , так как точка М принадлежит прямой OL, то
. Построим систему координат 0x1y1z1 . Обозначим координаты точки М через x1y1z1 , так как точка М принадлежит прямой OL, то ,
,  ,
,  ,
, (3)
(3)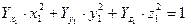 (4)
(4) то равенство (4) можно записать следующим образом
то равенство (4) можно записать следующим образом  что соответствует каноническому уравнению эллипсоида. Поэтому поверхность, соответствующая равенствам (1) и (2) получила название эллипсоида инерции. Для эллипсоида инерции главные оси инерции являются осями симметрии. Моменты инерции относительно этих осей имеют экстремальные значения.
что соответствует каноническому уравнению эллипсоида. Поэтому поверхность, соответствующая равенствам (1) и (2) получила название эллипсоида инерции. Для эллипсоида инерции главные оси инерции являются осями симметрии. Моменты инерции относительно этих осей имеют экстремальные значения.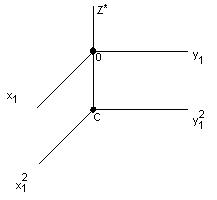
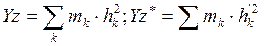
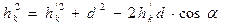 ;
; получаем
получаем  ;
;