Результаты ЕГЭ по математике выпускников 2014 года

XXIV гимназическая научно-практическая конференция

Секция «Физмат»

Решение стереометрических задач повышенной сложности

Домнышев Андрей Алексеевич

МБ НОУ «Гимназия №62»,

11 «А» класс

Научный руководитель:

Матысон Надежда Николаевна,

учитель математики МБ НОУ «Гимназия №62»

г. Новокузнецк, 2016 год

Содержание

1. ВВЕДЕНИЕ ...…………………………………………………………..………3

2. ОСНОВНАЯ ЧАСТЬ...…………………………………………………………4

2.1. Исследование результатов экзаменов прошлых лет………...……....4

2.2. Классификация стереометрических задач повышенной

сложности в задании №14…………………………………………...….…7

2.3. Алгоритм решения задач традиционным и

координатно-векторным методом……...…………………………………9

2.4 Решение задач различными методами………………………………11

3.ЗАКЛЮЧЕНИЕ…………………………………………..……………………14

4. Список использованных источников информации ………………………...15

5. Приложения…………………………………………………………………...16

ВВЕДЕНИЕ

Школьный курс геометрии состоит из двух частей: планиметрии и стереометрии. В планиметрии изучаются свойства геометрических фигур в плоскости. Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Именно при изучении и решении задач второго раздела у учащихся возникают определённые затруднения. Решение стереометрических задач, кроме знания теории, требует хорошо развитого пространственного и творческого мышления. Актуальность исследования стереометрических задач подкрепляется и тем, что с таким типом задач столкнутся одиннадцатиклассники на государственной итоговой аттестации.

В течение всей старшей школы идёт интенсивная подготовка учащихся к сдаче государственной итоговой аттестации в формате единого государственного экзамена. Двумя обязательными предметами являются математика и русский язык. С 2015 года произошло разделение экзамена по математике на базовый и профильный уровни. В зависимости от специальности, на которую абитуриенты планируют поступить, они выбирают уровень. Для большинства учащихся нашей гимназии приоритетный уровень – профильный.

За задание №14 (С2) профильного уровня ЕГЭ по математике можно получить 2 первичных балла. Первичные баллы переводятся в тестовые (проценты) по специальной шкале (см. приложение). Задание №14 не является заданием повышенной сложности (оно является всего лишь седьмым заданием из двенадцати второй части ЕГЭ по математике) и является доступным большинству школьников. Актуальность исследования подтверждается также тем, что при правильном выполнении первых четырнадцати заданий ЕГЭ по математике, учащийся набирает достаточное количество баллов для оценки «5». Так как задание №14 является менее трудным, чем последующие задания, то для многих сдающих профильный уровень это задание является единственной возможностью получить пятёрку за экзамен по математике.

С чего начать выполнение задания №14, какие методы решения существуют, какой теоретический материал нужно использовать – эти вопросы будут рассмотрены в данной работе.

Объект исследования:стереометрические задачи повышенной сложности.

Предмет исследования:задания №14 (С2) ЕГЭ по математике.

Цель работы: сделать задание №14 (С2) ЕГЭ по математике доступным для большинства школьников.

Задачи:

§ Исследовать результаты экзаменов выпускников прошлых лет;

§ Исследовать текущий уровень возможности учащихся выполнять задание №14 (С2) в гимназии;

§ Узнать о возможных методах решения задания №14 (С2);

§ Составить алгоритм выполнения задания №14 (С2);

§ Подобрать теоретический материал для решения задания №14 (С2);

§ Научиться использовать полученные знания на практике;

§ Помочь учащимся воспользоваться результатами исследовательской работы для подготовки к ЕГЭ.

Методы, использованные в работе: исследование, сравнение, изучение, обобщение, классификация, анкетирование, анализ.

Основные этапы:

1) Постановка целей и задач;

2) Исследование объекта путём анкетирования;

3) Сбор сведений об объекте исследования с помощью различных источников;

4) Обобщение полученных сведений;

5) Подведение итогов;

6) Составления справочника для учащихся.

ОСНОВНАЯ ЧАСТЬ

Исследование результатов экзаменов прошлых лет

Для получения более объективной картины анализа выполнения задания №14 необходимо проанализировать результаты ЕГЭ по математике нескольких предыдущих выпусков и их динамику. Помимо задания №14 2 первичных балла можно получить за задания №13 и №15. Задание №16 также является геометрическим (раздел планиметрия). Таким образом были проанализированы результаты выпусков 2013, 2014 и 2015 годов по заданиям С1, С2, С3 и С4.

Результаты ЕГЭ по математике выпускников 2013 года

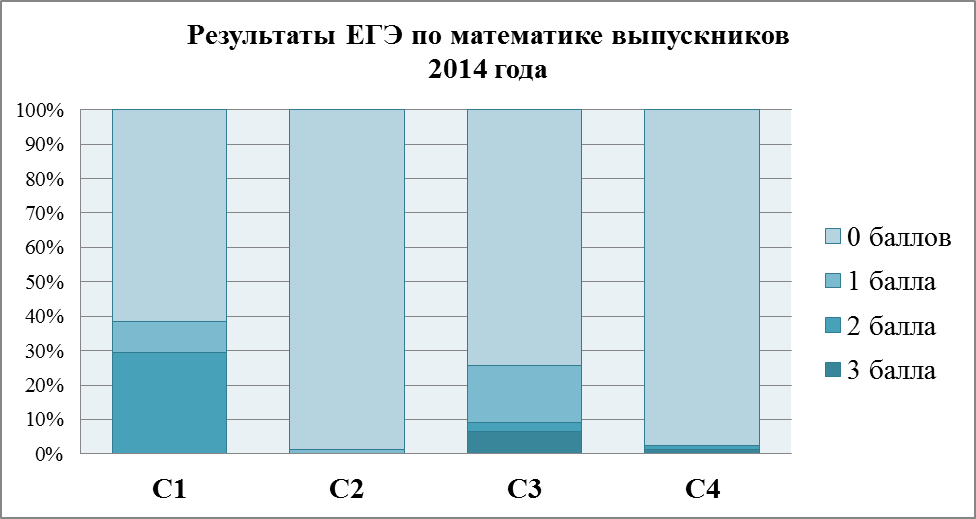
Результаты ЕГЭ по математике выпускников 2014 года

Не нашли, что искали? Воспользуйтесь поиском по сайту: