
|
|
Вынужденные колебания. Резонанс.Виды дифференциальных уравнений. Интеграл дифференциального уравнения. Общий интеграл. Интегральная кривая.
Задача Коши. Существование и единственность решения.
Простейшие ОДУ первого порядка, разрешенные относительно производной.
Уравнения с разделяющимися переменными.
5. Уравнения вида
Однородное уравнение.
Уравнение в полных дифференциалах.
Уравнение, допускающее интегрирующий множитель
P(x,y)dx + Q(x,y)dy = 0 Если
μ(х,у)P(x,y)dx + μ(х,у)Q(x,y)dy = 0, так чтобы выполнялось условие Эйлера:
Далее
Линейные обыкновенные дифференциальные уравнения первого порядка. Метод Лагранжа.
Уравнение Бернулли.
Уравнение Риккати.
Уравнение Лагранжа.
Уравнение Клеро.
Дифференциальные уравнения порядка выше первого. Случаи понижения по
Случай 3:
Пример:
15. Линейные дифференциальные уравнения n‑го порядка. Вронскиан. Фундаментальная система решений.
Однородные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение.
Линейные неоднородные уравнения. Отыскание частного решения в случае уравнения с квазиполиномом. 18. Линейные неоднородные уравнения. Отыскание частного решения методом вариации произвольных постоянных.
Одномерное движение. Гармонические колебания. Колебания груза на пружине. Колебания математического маятника (случай чисто гармонических колебаний). Одномерное движение.В этом случае уравнение движения можно проинтегрировать до конца и выразить ответ чеpезинтегpал, или, как говоpят в квадратурах. Легче всего это сделать, воспользовавшись законом сохранения энергии
Поскольку кинетическая энергия всегда положительна, то неравенство Ниже, на pис. 7, показан пример. Согласно этому пpимеpу, движение может происходить лишь на конечном отрезке xA< x <xB, что соответствует финитному движению и в полубесконечном интервале . В последнем случае движение инфинитно, так как частица может уходить на бесконечность. Точки xA, xB и xC называют точками остановки, поскольку скорость в них обращается в нуль.
Рис. 7. Гpаницы движения в одномеpном случае. Hайдемтепеpь зависимость кооpдинаты x от вpемени t. Для этого выразим из уравнения (25) скорость
Это есть дифференциальное уравнение с разделяющими переменными, которое можно легко проинтегрировать (то есть pешить):
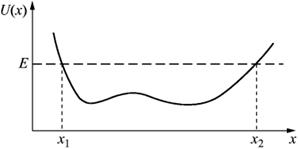
Рис. 8. Пеpиодическое движение. В случае финитного движения, которое мы сейчас рассмотрим, можно вычислить период движения как функцию энергии системы E (см. pис. 8): где x1 и x2 — точки поворота, где скорость обращается в нуль, то есть E = U(x). Применим теперь эту формулу в качестве примера для движения в поле
В этом случае
Рис. 9. Движение в квадpатичном потенциале. Гаpмонические колебания.
Введем тепеpь новую переменную интегрирования Тогда
то есть в этом случае получается известная формула для периода колебаний грузика на пружине, который не зависит от энергии (так называемые гармонические колебания). Во всех остальных случаях период колебаний зависит от энергии системы (ангармонические колебания).
Затухающие колебания. Декремент затухания. Случай апериодического движения.
Вынужденные колебания. Резонанс. Дифференциальное уравнение вынужденных колебаний (механических) и его решение по гармоническому закону:
Эту систему можно представить в виде:
Система обыкновенных дифференциальных уравнений вида
где aij(x) и bi (x) — известные, а yj (x) — неизвестные функции, (i = 1,2, … ,n, j = 1,2, n) называется линейной системой дифференциальных уравнений. При описании линейных систем дифференциальных уравнений удобнее пользоваться векторной (матричной) формой записи. Обозначим
Тогда линейная система дифференциальных уравнений в векторной (матричной) форме записывается в виде Y' = A(x)Y + b(x) или, что то же самое, в виде:
Если A(x) и b(x) непрерывны на отрезке [a, b] , то какова бы ни была начальная точка (x0, Y0) из Rn + 1, задача Коши Y' = A(x)Y + b(x), Y(x0) = Y0,имеет единственное на [a,b] решение Y = Y(x) Важно отметить, что для линейной системы дифференциальных уравнений разрешимость задачи Коши глобальная: решение существует всюду, где непрерывны коэффициенты и неоднородность системы. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|














 ,
,  .
.




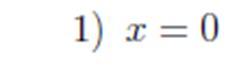











 домножим на μ(х,у):
домножим на μ(х,у):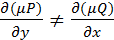

 ð
ð 


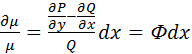 , Ф=ф(х).
, Ф=ф(х).


 подставляется в
подставляется в 











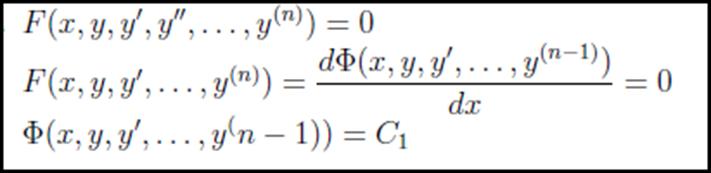

























 (25)
(25) (26) определяет классически доступные области движения (границы движения) в одномерном случае. Другими словами, движение может происходить лишь в областях пространства, где E > U(x).
(26) определяет классически доступные области движения (границы движения) в одномерном случае. Другими словами, движение может происходить лишь в областях пространства, где E > U(x).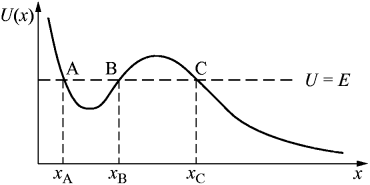
 (27)
(27) (28)
(28)
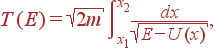 (29)
(29) (30)
(30) (см. pис. 9), поэтому
(см. pис. 9), поэтому


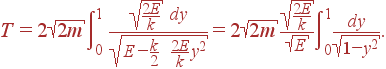
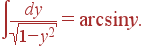
















 При рассмотрении механических колебаний, то роль X(t) играет внешняя вынуждающая сила
При рассмотрении механических колебаний, то роль X(t) играет внешняя вынуждающая сила  (1) С учетом (1) закон движения для пружинного маятника запишется как
(1) С учетом (1) закон движения для пружинного маятника запишется как  Используя формулу для циклической частоты свободных незатухающих колебаний прижинного маятника и (10) предыдущего раздела, получим уравнение
Используя формулу для циклической частоты свободных незатухающих колебаний прижинного маятника и (10) предыдущего раздела, получим уравнение  (2) Колебания, которые возникают под действием внешней периодически изменяющейся силы называются соответственно вынужденными механическими колебаниями. Уравнения (2) и (4) приведем к линейному неоднородному дифференциальному уравнению
(2) Колебания, которые возникают под действием внешней периодически изменяющейся силы называются соответственно вынужденными механическими колебаниями. Уравнения (2) и (4) приведем к линейному неоднородному дифференциальному уравнению  (5)Решение уравнения (5) будет равно сумме общего решения (5) однородного уравнения (1) и частного решения неоднородного уравнения. Частное решение ищем в комплексной форме. Заменим правую часть уравнения (5) на комплексную переменную х0eiωt :
(5)Решение уравнения (5) будет равно сумме общего решения (5) однородного уравнения (1) и частного решения неоднородного уравнения. Частное решение ищем в комплексной форме. Заменим правую часть уравнения (5) на комплексную переменную х0eiωt :  (6) Частное решение данного уравнения будем искать
(6) Частное решение данного уравнения будем искать  Подставляя выражение для s и его производных (
Подставляя выражение для s и его производных ( 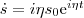 и
и  ) в выражение (6), найдем
) в выражение (6), найдем  (7) Поскольку это равенство должно быть верным для всех моментов времени, то время t из него должно исключаться. Значит η=ω. Учитывая это, из формулы (7) найдем величину s0 и умножим ее числитель и знаменатель на (ω02 - ω2 - 2iδω)
(7) Поскольку это равенство должно быть верным для всех моментов времени, то время t из него должно исключаться. Значит η=ω. Учитывая это, из формулы (7) найдем величину s0 и умножим ее числитель и знаменатель на (ω02 - ω2 - 2iδω) Это комплексное число представим в экспоненциальной форме:
Это комплексное число представим в экспоненциальной форме:  где
где 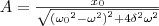 (8)
(8) 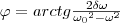 (9)
(9)  Его вещественная часть, которая является решением уравнения (5), равна
Его вещественная часть, которая является решением уравнения (5), равна  (10) где А и φ определяются соответственно формулами (8) и (9). Следовательно, частное решение неоднородного уравнения (5) равно
(10) где А и φ определяются соответственно формулами (8) и (9). Следовательно, частное решение неоднородного уравнения (5) равно 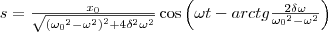 Решение уравнения (5) есть сумма общего решения однородного уравнения
Решение уравнения (5) есть сумма общего решения однородного уравнения 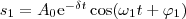 (12)
(12) 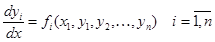 1)Система такого вида называется нормальной системой дифференциальных уравнений (СНДУ). Для нормальной системы дифференциальных уравнений можно сформулировать теорему о существовании и единственности такую же, как и для дифференциального уравнения.Теорема. Если функции
1)Система такого вида называется нормальной системой дифференциальных уравнений (СНДУ). Для нормальной системы дифференциальных уравнений можно сформулировать теорему о существовании и единственности такую же, как и для дифференциального уравнения.Теорема. Если функции  определены и непрерывны на открытом множестве
определены и непрерывны на открытом множестве  , а соответствующие частные производные
, а соответствующие частные производные  тоже непрерывны на
тоже непрерывны на 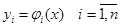 (2) а при наличии начальных условий
(2) а при наличии начальных условий  (3) это решение будет единственным.
(3) это решение будет единственным. (4)
(4)

 Матрица A называется матрицей системы, а вектор–функция b(x) — неоднородностью системы.Система Y' = A(x)Y + b(x) называется неоднородной линейной системой дифференциальных уравнений, а система Y' = A(x)Y— однородной линейной системой. Справедлива следующая теорема существования и единственности решения задачи Коши для линейной системы дифференциальных уравнений.
Матрица A называется матрицей системы, а вектор–функция b(x) — неоднородностью системы.Система Y' = A(x)Y + b(x) называется неоднородной линейной системой дифференциальных уравнений, а система Y' = A(x)Y— однородной линейной системой. Справедлива следующая теорема существования и единственности решения задачи Коши для линейной системы дифференциальных уравнений.