
|
|
Моделирование сезонной составляющей при помощи фиктивных переменных.Сезонная составляющая - некоторая периодическая функция времени с периодом в один год. Рассмотрим популярную в эконометрике периодическую функцию дискретного времени с периодом τ. Уравнение этой функции: S(t+τ)=S(t) S(t)=
Поясним смысл этих переменных на примере квартальных данных(когда τ=4). d1={1- для первого квартала, 0- для других кварталов}; d2={1- для второго квартала, 0 - для других кварталов}; d3={1- для третьего квартала, 0 - для других кварталов}
При помощи модели (*) можно моделировать не только сезонную составляющую, но и влияние на соответствующую эндогенную переменную качественного фактора, который способен находиться в одном из τ состояний. Состояние этого фактора, при котором все фиктивные переменные равны 0 называется базовым.(В нашем примере- это четвертый квартал года ) Регрессионная зависимость случайных переменных. Функция регрессии, стандартные модели функции регрессии. Модели, в состав которых входят случайные возмущения, отражающие воздействие на эндогенные переменные неучтенных факторов принято называть эконометрическими (регрессионными). В общем случае структурная форма эконометрической модели имеет вид: F( Структурная форма: А Приведенная форма модели в общем случае имеет вид:
Этапы построения эконометрических моделей: 1.Спецификация модели 2.Сбор и проверка статистической информации 3.Оценивание модели 4.Проверка адекватности ЛММР
Объясняющие переменные Схема Гаусса–Маркова (на примере модели Оукена). Модель Оукена: t=1,2,... где wt - темп прироста безработицы в году t, yt - темп роста ВВП
Пусть в рамках исследуемой модели величины связаны следующим образом:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова ( где
Оценку вектора обозначим где f(· , ·) – символ процедуры. Данная процедура именуется линейной относительно вектора
Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные статистические процедуры. Требования к наилучшей статистической процедуре. Пусть имеется выборка
значений переменных x и y модели
Данная выборка получена на этапе наблюдения и предназначена для оценивания параметров модели
В рамках данной модели величины (*) связаны следующей СЛОУ:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова. Вот компактная запись этой схемы где
Наконец, Оценку вектора обозначим где f(· , ·) – символ процедуры. Данная процедура именуется линейной относительно вектора
Класс таких всевозможных линейных процедур оценивания по исходной выборке вектора Наилучшая процедура f*(· , ·) из выбранного класса процедур F должна генерировать оценку
21. Теорема Гаусса-Маркова: выражение вектора оценок коэффициентов Если справедливы все предпосылки теорему Гаусса-Маркова, тогда имеет место утверждение А: Доказательство: Шаг 1. Шаг 2.
22. Теорема Гаусса-Маркова: выражение Cov( Одним из утверждений Гаусса-Маркова является утверждение D:
Обоснование. Пусть выполнены все предпосылки теоремы Гаусса-Маркова. Тогда ковариационная матрица вектора случайных остатков в уравнениях наблюдений является диагональной и конкретно скалярной: Видим, что оценки коэффициентов модели являются линейным преобразованием вектора Из вида вектора
23. Теорема Гаусса-Маркова: предпосылки и свойство наименьших квадратов Рассмотрим уравнения наблюдений вида Предпосылки теоремы Гаусса-Маркова для данных уравнений: 1. Ожидаемые значения случайных возмущений равны нулю: E(u1)=…=E(un)=0. 2. Дисперсии случайных остатков одинаковые и не зависят от объясняющих переменных: Var(u1)=…=Var(un)= 3. Случайные остатки в уравнениях наблюдений попарно некоррелированы: 4. Значения объясняющих переменных не коррелированы со значениями случайных возмущений: Cov(xij,ui)=0. Тогда выполняются необходимые утверждения (не все, только те, которые требуются в вопросе): А: С. Оценки, вычисленные в А, обладают замечательным свойством наименьших квадратов, то есть
24. Теорема Гаусса-Маркова: выражение Представим ситуацию, когда предпосылка 2 теоремы Гаусса-Маркова о гомоскедастичности случайного остатка не выполнена, то есть дисперсия зависит от объясняющих переменных, а остаток гетероскедастичен. В таком случае оценки параметров модели утрачивают свое свойство оптимальности (свойство минимальных дисперсий). Для построения оптимальной процедуры оценивания модели с гетероскедастичным остатком потребуется модель гетероскедастичности остатка, вот простейший вид такой модели: В этой модели присутствуют две константы – положительная константа Если в модели веса воспользоваться моделью гетероскедастичности, то вес случайного остатка будет вычисляться по вышеуказанному правилу. В выражении веса константа

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (t)+
(t)+  (t)+…+
(t)+…+  (t) (*)
(t) (*) ,…
,… 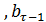 - коэффициенты
- коэффициенты (t),…,
(t),…,  (t)-функции времени, которые в данной ситуации имеют смысл индикаторов сезонов (конкретно кварталов) и служат примером фиктивных переменных (переменные, значения которых выбираются исследователями по договоренности)
(t)-функции времени, которые в данной ситуации имеют смысл индикаторов сезонов (конкретно кварталов) и служат примером фиктивных переменных (переменные, значения которых выбираются исследователями по договоренности) ,
,  )=
)= 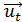
 =
= 
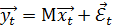

 в общем случае не зависят от случайного остатка
в общем случае не зависят от случайного остатка  . Данная модель является базовой моделью эконометрики, потому что к такому виду может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения.
. Данная модель является базовой моделью эконометрики, потому что к такому виду может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения.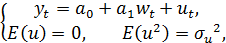
 , причём
, причём 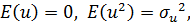
 ). Вот компактная запись этой схемы
). Вот компактная запись этой схемы 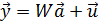
 - вектор известных значений эндогенной переменной yt модели;
- вектор известных значений эндогенной переменной yt модели; - вектор неизвестных значений случайных возмущений ut;
- вектор неизвестных значений случайных возмущений ut; - матрица известных значений предопределенной переменной wt модели, расширенная столбцом единиц;
- матрица известных значений предопределенной переменной wt модели, расширенная столбцом единиц; – вектор неизвестных коэффициентов уравнения модели.
– вектор неизвестных коэффициентов уравнения модели. . Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим:
. Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим: 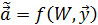
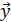 значений эндогенной переменной yt, если:
значений эндогенной переменной yt, если:  .
. , где матрица коэффициентов, зависящих только от выборочных значений W предопределенной переменной wt
, где матрица коэффициентов, зависящих только от выборочных значений W предопределенной переменной wt
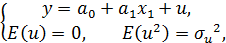
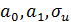
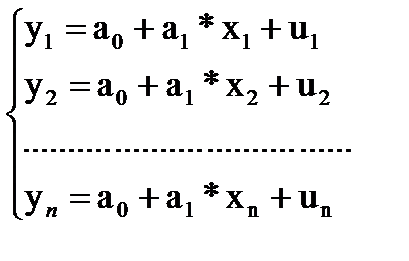
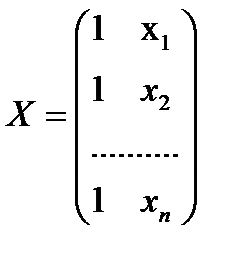 - матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0);
- матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0);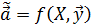
 .
. обозначим символом F.
обозначим символом F. , которая обладает одновременно двумя свойствами: ожидаемая оценка параметра совпадает с истинным значением
, которая обладает одновременно двумя свойствами: ожидаемая оценка параметра совпадает с истинным значением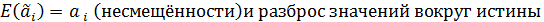
 , i=0,1 (эффективности).
, i=0,1 (эффективности). и доказательство их несмещённости.
и доказательство их несмещённости. – оптимальная линейная процедура оценивания коэффициентов функции регрессии. Докажем, что имеет место свойство несмещенности оценок коэффициентов, то есть
– оптимальная линейная процедура оценивания коэффициентов функции регрессии. Докажем, что имеет место свойство несмещенности оценок коэффициентов, то есть  .
. .
. , ч.т.д.
, ч.т.д. , где
, где  – диагональный элемент матрицы
– диагональный элемент матрицы  . В матричном виде можно представить так (так показано в учебнике)
. В матричном виде можно представить так (так показано в учебнике)  .
. где I – единичная матрица. Теперь обратимся к утверждению А теоремы Гаусса-Маркова:
где I – единичная матрица. Теперь обратимся к утверждению А теоремы Гаусса-Маркова:  . Это значит, что мы можем воспользоваться теоремой Фишера при расчете ковариационной матрицы:
. Это значит, что мы можем воспользоваться теоремой Фишера при расчете ковариационной матрицы:  , где
, где  . С учетом вида матрица А и выполненных действий, мы пришли к исходному виду ковариационной матрицы вектора
. С учетом вида матрица А и выполненных действий, мы пришли к исходному виду ковариационной матрицы вектора  .
.
 -> min.
-> min. .
. .
. . Именно это свойство является причиной общепринятого названия процедуры А – МНК.
. Именно это свойство является причиной общепринятого названия процедуры А – МНК.  .
. .
. и показатель степени λ. Параметр λ подбирается в итоге проведения теста Голдфилда-Квандта из множества значений ±0,5, ±1, ±2 так, чтобы тест Голдфилда-Квандта просигнализировал о гомоскедастичности остатка в преобразованной ЛММР. (Заметим, что если остаток λ=0, то остаток в модели гомоскедастичен и константа
и показатель степени λ. Параметр λ подбирается в итоге проведения теста Голдфилда-Квандта из множества значений ±0,5, ±1, ±2 так, чтобы тест Голдфилда-Квандта просигнализировал о гомоскедастичности остатка в преобразованной ЛММР. (Заметим, что если остаток λ=0, то остаток в модели гомоскедастичен и константа  ).
).  .
.