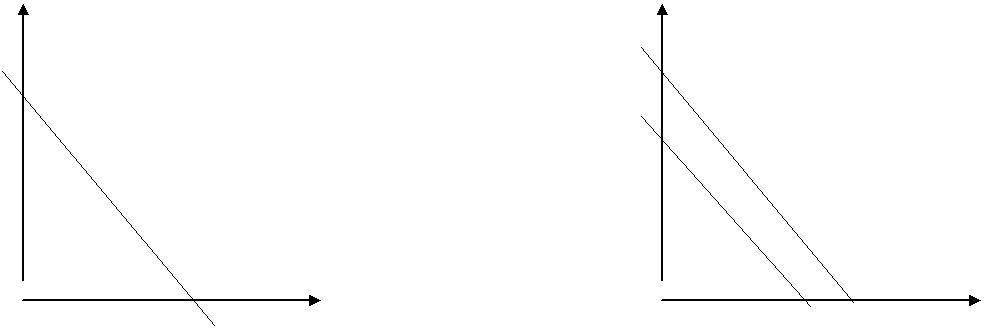|
|
Выбор лотерей при их распределении
Как группе индивидуумов следует выбирать из лотерей, когда имеется возможность распределения риска? Пусть двум участникам нужно сделать выбор из двух лотерей l′ и l′′.
При многократных принятиях решения точка с неоптимальна по Парето, т.к. предпочтительнее использовать рандомизированную процедуру. Эта рандомизированная процедура имеет совместную оценку посредине между a и b, и поэтому оба участника предпочтут ее точке с.
Аналогично на рис.15. в не существует никакого совместно приемлемого распределения l′ или l′′, однако, рандомизируя между точками a и b можно получить совместно приемлемое распределение, использующее l′ и l′′.
Рассмотрим теперь частный случай двух участников с экспоненциальными функциями полезности с параметрами с1 и с2. Выше мы показали, что оптимальное по Парето распределение любой лотереи l включает в себя побочный платеж b и распределение лотереи на пропорциональные доли: ρ1=с1/(c1+c2), ρ2=c2/(c1+c2). Пусть ρ1l и ρ2l означает доли лотереи l,предназначенные индивидуумам 1 и 2 соответственно. Тогда:
участнику 1 предназначается [ - b+лотерея ρ1l]; участнику 2 предназначается [ +b+лотерея ρ2l]. Отсюда45
БДЭ1([ - b+лотерея ρ1l])= - b+a1, где а1=БДЭ1(ρ1l); БДЭ2([ +b+лотерея ρ2l])= +b+a2, где а2=БДЭ2(ρ2l).
Таким образом, пара БДЭ для этого разбиения равна ( - b+a1, +b+a2). Поскольку b можно выбрать произвольно (это зависит от выбора оптимальной по Парето точки на контуре, с помощью λ1, λ2 >0, λ1 +λ2 =1),то пара ( - b+a1, b+a 2 ) “заметает”целую прямую,которая изображена на рис.16. БДЭ2 БДЭ2
(0, а1+а2) (0, а1+а2)
(0, a1+a2)
• ( - b+a1, b+a2) • (a1, a2)
(a +a , 0) (a +a , 0) (a +a , 0) БДЭ1 БДЭ1 Рис.16 Рис.17 Предположим, у участников есть выбор между лотереями l′ и l′′. Соответствующие прямые изображены на рис.17. В этом конкретном случае, очевидно, никогда не оптимально выбирать лотерею l′, если доступна l′′.
Таким образом можно заключить, что если мы можем выбирать между лотереями, то нам следует выбрать так, чтобы максимизировать показатель БДЭ1(ρ1l)+БДЭ2(ρ2l).
45 Как известно [9], экспоненциальная функция полезности обладает тем свойством, что при увеличении всех платежей лотереи на некоторую постоянную БДЭ новой лотереи увеличивается по сравнению с БДЭ старой на ту же величину .
где БДЭ*(l) есть БДЭ лотереи l, определенный для функции полезности u*(x)=1 - exp( - x/c*), где с*=с1+с2. Д о к а з а т е л ь с т в о. Пусть l - лотерея, у которой выигрыш х является случайной величиной. Сначала мы покажем, что если функция полезности индивидуума равна u(x)=1 - e-x/c, то БДЭ лотереи ρl,
где М - как обычно, оператор математического ожидания. Чтобы доказать это, положим БДЭ(ρl)=d, тогда по определению 1 - e-d/c = M(1 - e-ρx/c) = 1 - M(e-ρx/c). Отсюда получаем формулу (10). С помощью формулы (10), и заметив, что ρ1/c1 = ρ2/c2 = 1/(c1+c2)=1/c*, получаем БДЭ1(ρ1l) = - c1 log((M(exp( - ρ1x/c1))) =- c1 log(M(exp( - x/c*))), БДЭ2(ρ2l) = - c2 log(M(exp( - ρ2x/c2))) = -c2 log(M(exp( - x/c*))). Складывая, получаем БДЭ1(ρ1l)+БДЭ2(ρ2l) = - c* log(M(exp( - x/c*))), и, с учетом (10), правая часть этого выражения равняется БДЭ*(l). Таким образом, если допустимо распределение риска и если у участников 1 и 2 экспоненциальные функции распределения с параметрами с1 и с2 соответственно, то уместно производить выбор между лотереями, используя групповую экспоненциальную функцию полезности u* с параметром с*=с1+ с2. Этот результат не зависит ни от того, рассматриваем ли мы задачу в виде задачи торга или образования синдиката, ни от выбора пары (λ1 ,λ 2 ), которая задает точку на границе. Более того, этот результат обобщается на случай более чем 2-х участников. Например, если у 10-ти индивидуумов экспоненциальные функции полезности с одинаковым параметром с=1000, то им следует всем вместе вести себя как единственному участнику с экспоненциальной полезностью с параметром с*=10000 (его поведение близко к поведению объективиста,см.п.3.4.).
В частном случае, когда лотерея l дает неизвестный платеж, который распределен нормально с математическим ожиданием μ и стандартным отклонением σ , можно показать, что БДЭ лотереи ρl для экспоненциальной функции полезности с параметром с равняется БДЭ(ρl)=ρμ -(ρσ )2/(2c), следовательно БДЭ1(ρ1l)+БДЭ2(ρ2l)=[ ρ1μ - (ρ1σ )2/(2c1)]+[ ρ2μ - (ρ2σ )2/(2c2)]= μ - σ2/(2c*).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Две кривые, обозначенные на рис.15 А′ и А′′ - это оптимальные по Парето границы для лотерей l′ и l′′ соответственно. Из рис.15.а видно, что l′′ лучше чем l′. Для рис.15.б в общем случае нельзя сказать, что лучше. Однако, если выбор производит участник 1 с возможностью предложить долю 2 (случай синдиката), то он мог бы выбрать l′ и разбить ее так, чтобы получить точку а; если однако 2 - основной участник, принимающий решение, то он мог бы выбрать l′′ и распределить ее так, чтобы получить b.
Две кривые, обозначенные на рис.15 А′ и А′′ - это оптимальные по Парето границы для лотерей l′ и l′′ соответственно. Из рис.15.а видно, что l′′ лучше чем l′. Для рис.15.б в общем случае нельзя сказать, что лучше. Однако, если выбор производит участник 1 с возможностью предложить долю 2 (случай синдиката), то он мог бы выбрать l′ и разбить ее так, чтобы получить точку а; если однако 2 - основной участник, принимающий решение, то он мог бы выбрать l′′ и распределить ее так, чтобы получить b.