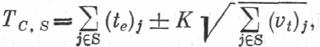Задачи распределения и добавления ресурсов

Задачами распределения ресурсов, по существу, являются задачи определения сроков исполнения проекта, при которых возможно либо выравнивание потребности в ресурсах при соблюдении ограничений на длительность выполнения проекта, либо минимизация длительности выполнения проекта при ограничениях на трудовые ресурсы, либо минимизация общей стоимости ресурсов и штрафов за задержку выполнения проекта.

Выравнивание использования ресурсов.Предположим,что для выполнения каждой из работ1-3, 1 -5, 1-2 и 2-4 (рис.)требуется один исполнитель,который будет занят полный рабочий день.Вместе стем имеются только два исполнителя. Ограничение , накладываемое на трудовые ресурсы (два исполнителя), может быть удовлетворено без продления времени завершения проекта, если задержать на 8 ед. времени начало работы 1-3 (оно может быть задержано до 14 ед. времени без задержки завершения проекта). Другой возможный вариант состоит в выполнении каждой из работ 1-3 и 1- 2 с меньшей скоростью ( например, соответствующей половине возможностей человека) при условии, что время их завершения увеличится вдвое.

Сокращение кратчайшего пути.Не менее важная роль отводится резервному времени присокращении длительности критического пути (путей) . Предположим, что допускается перемещение исполнителей работ 1-3 и 1-2 на работу 1-5 (рис. ). В результате этого произошла бы задержка работ 1-3 и 1-2, тогда как продолжительность работы 1-5 на критическом пути сократилась.Оптимальноерешение достигается либо когда ни один исполнитель не может быть перемещен на другую работу, так как все резервное время ликвидировано, либо когда нельзя больше сократить критический путь за счет перераспределения ресурсов с работы, имеющей резерв времени, на критическую.

Использование дополнительных ресурсов.Единственный способ сокращения критическогопути, после того как перераспределение всех ресурсов между работами, имеющими резервное время, и работами критического пути уже выполнено, заключается в использовании дополнительных ресурсов. Выполнение некоторых работ критического пути, по-видимому, может быть ускорено путем увеличения общего бюджета, например путем привлечения дополнительных ресурсов из внешних по отношению к данному проекту источников.

Предположим, что некоторая конкретная работа критического пути, которая в нормальных условиях стоит С_п и занимает t_n ед. времени, может быть выполнена за t_i времени при стоимости С_i, где t_i< t_n иC_i >С_п. Используя приращения стоимости,т.е. C = C_i— С_п, можно получить кусочно-линейную аппроксимацию функции С = f(t), которая обычно имеет наклон вправо (уменьшение t с увеличением С).

Анализ основывался на величине средней стоимости сокращения длительности работ на единицу

сокращение длительности проекта на единицу при минимальном увеличении общих прямых затрат.

Поскольку сокращение длительности проекта приводит к уменьшению косвенных затрат на проект, этот процесс обычно продолжается до тех пор, пока сумма изменяющихся в противоположных

направлениях прямых и косвенных затрат не достигнет минимума, который определяет оптимальный (относительно общих затрат) график выполнения проекта.

Комплексные проекты

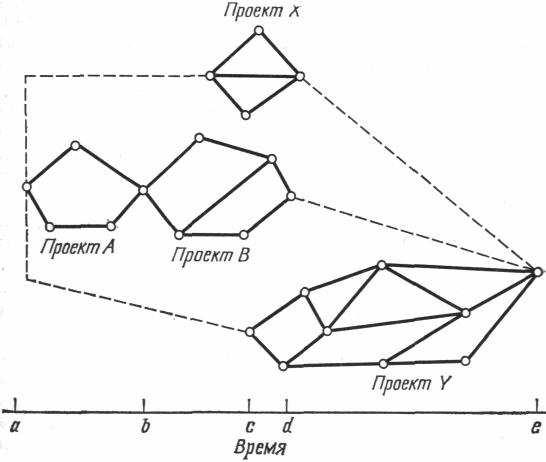
Рассмотренные выше сетевые методы могут быть применены к планированию нескольких проектов, руководство которыми осуществляется одной организацией. Рассмотрим, например, пор-тфель из четырех проектов (рис. ). Как видно из рисунка, проект А должен быть завершен до того, как сможет начаться проект В ( например, проект А должен произвести сырье для проекта В). Проект X и проект Y могут начаться и закончиться в любое время в интервале между моментами а и е. Таким образом, пунктирные линии на рис. отображают лишь фиктивные зависимости и служат для того, чтобы указать общий диапазон времени для всех четырех проектов. Резервное время для отдельных проектов, образующееся за счет этих фиктивных работ, можно использовать так же, как фиктивные работы в сетях для автономного проекта.

Рис. Сетевой график для комплексной программы

Предположим, например, что проекты В и X используют одни и те же ресурсы и что потребность в этих ресурсах превышает их наличие в случае необходимости одновременной реализации проектов В и X. Из рис. видно, что начало проекта X можно задержать до момента d, сосредоточив все ресурсы полностью на проекте В. После того как проект В будет завершен, эти ресурсы можно будет использовать для выполнения проекта X.

Другая возможность состоит в том, чтобы оба проекта использовали эти ресурсы с пониженной интенсивностью и при этом оба проекта будут задерживаться (на столько, чтобы не выйти за пределы момента е). Процедуры ускорения выполнения работ за счет повышения затрат, описанные ранее, могут быть применимы и к отдельным проектам. Таким образом, методы сетевого планирования для комплексных проектов полностью аналогичны сетевым методам, применяемым для отдельных проектов.

Вообще говоря, последовательные изменения в сетевых графиках проектов позволят руководителям на уровне проекта и на уровне отдела создавать интегрированные планы . Руководитель каждого проекта может представить на рассмотрение оптимальный сетевой график. Эти графики могут быть затем объединены в одну сеть комплексного проекта [65], на основе чего разработано несколько графиков для комплексного проекта при различных предположениях относительно приоритетов, ресурсов и т. д.

Стохастические подходы

Часто возникает необходимость оценить вероятность того, будет ли отдельная работа, некоторая совокупность работ или проект в целом закончены к определенному сроку. Подобная формулировка задачи, которая была основой при первоначальной разработке метода ПЕРТ, предполагает использование трех видов оценок длительности каждой работы в сети: t₀ — оптимистической оценки длительности, t_m — модальной оценки, т. е. оценки наиболее вероятной длительности, и t_p —

пессимистической оценки длительности. Предполагается, что гипотетическое распределение фактической длительности выполнения работы описывается β-распределением. Математическое ожидание t_e и дисперсия v_t для β-распределения, определяющиеся выражениями t_e = (t₀ + 4t_m + t_p)/6, v_t = [(t_p

— t₀)/6]² , могут быть вычислены для каждой работы сети. В этом случае ожидаемое время завершения Т_е всего проекта находится как сумма величин t_e (которые аналогичны длительностям работ прииспользовании метода критического пути) для работ, составляющих путь наибольшей длины через сеть. Далее для любого подмножества критических работ S могут быть вычислены доверительные границы длительности по следующей формуле (которая основана на центральной предельной теореме для суммы независимых случайных величин):

где К — константа, зависящая от степени достоверности (К = 3 для степени достоверности 99,7%, К = 2 для степени достоверности95%и т.д.).Обычно«оптимальным»считается такой план выполненияпроекта , для которого Т_cs≤ DC_s , где DC — желательный срок завершения множества работ S. Для сетевых графиков, которые не удовлетворяют этому критерию, можно прибегнуть к перераспределению ресурсов с ненапряженных работ на критический путь, к увеличению затрат или более радикальным способам перепланировки проекта, пока не будет удовлетворено требование по этому критерию.

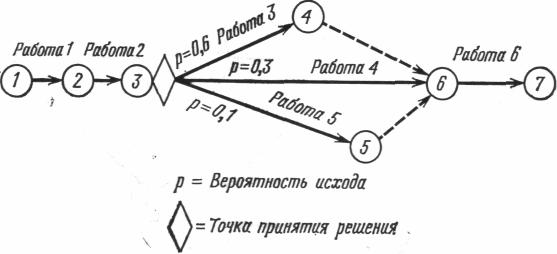
Многие проекты часто подвержены действию случайных факторов, т. е. состав работ, выполняемых после завершения некоторого этапа, может изменяться в зависимости от некоторых условий. Задачи этого типа можно изобразить с помощью сетей типа дерева с точками принятия решений (рис. ).

Заметим, что резервы времени 4-6 и 5-6 являются условными: если в узле 3 получен результат такой, что выбирается работа 3 или работа 5, то весь проект сокращается на соответствующую одному из имеющихся резервов величину. Все прочие расчеты сети производятся так же, как описано ранее, за исключением того, что результаты этих вычислений должны учитывать вероятность соответствующего результата. Например, на рис. 9 ожидаемое время завершения в узле 7 следует вычислять по формуле:

t_e⁶+(0,6t_e³+0,3t_e⁴+0,1t_e⁵)+t_e²+t_e¹где t_e^j —математическое ожидание длительностиj-й работы.

Рис. Сеть с возможными путями

Для проблем этого типа специально предназначен язык моделирования GERT.

Не нашли, что искали? Воспользуйтесь поиском по сайту: