
|
|
Как вычисляют разность стандартных химических потенциаловФизико-химические закономерности идеально-газовых реакций. Условия направленности и равновесия. Пусть имеется смесь веществ А, В, С, D, количество которых в исходном состоянии равно аА + вВ → сС + dD (1) если
Здесь Из соотношения (2) следует, что GТ,Р – монотонно убывающая функция ξ. Самопроизвольная реакция (1) продолжается до тех пор, пока GТ,Р убывает, и заканчивается наступлением состояния равновесия, в котором GТ,Р имеет минимальное значение (рис.1).
_______________________ * «е» – от сокращенного слова «equilibrium» – равновесие. На рис. 1 Найдем соотношение (2) в явном виде, воспользовавшись выражением химического потенциала i компонента в идеально газовой смеси:
где После преобразования
Определим (3) как функцию состава исходной системы, используя уравнение: Количество молей в исходном состоянии
Тогда
и
Введем обозначение тогда
или
где ∆ν = (c + d) – (a + b) Величина сС + dD → aA + bB. В ходе реакции отношение под знаком логарифма увеличивается, поскольку мольные доли продуктов хC и хD возрастают, а продуктов хА и хВ уменьшаются. В итоге при значении ξ = ξе производная становится равной нулю. Тогда
где в квадратных скобках – парциальные давления в состоянии равновесия. Из (5) следует
Обозначим количество молей i-ого вещества в состоянии равновесия через ni. Тогда общее количество молей
Для мольных долей в состоянии равновесия хi имеем
Тогда
Прежде чем провести дальнейший анализ соотношений (5) – (7) рассмотрим способы вычисления изменения стандартных химических потенциалов, Как вычисляют разность стандартных химических потенциалов Отметим, что по определению
Здесь, например, Тогда
или
Величина Из физико-химического смысла (8) – (9) следует, что аА + bB = cC + dD,
Отметим также, что в «реакции» (11) а молей А, b молей B полностью «превращаются» в с молей С и d молей D, при изменении ξ от нуля до единицы, ∆ξ=1. Аналогичная «реакция» имеется в виду при вычислении Непосредственно определить ∆G0 по уравнению (11) невозможно, поскольку неизвестны мольные абсолютные значения энергий Гиббса Энергия образования Гиббсова энергия образования это изменение энергии Гиббса в реакции образования данного соединения из простых веществ при стандартном давлении Р0=1 атм, при этом сами вещества и образующееся соединение находятся в стандартных состояниях. Например, S (тв, ромб.) + О2 (идеал. газ) = SO2 (идеал. газ) (12) T, P0 = 1 атм Данную реакцию можно осуществить экспериментально. Из приведенного примера следует, что реакция образования – это реакция, в которой вещества – реагенты полностью превращаются в соединение – продукт. Стандартность реакции (12) заключается в том, что задано определенное стандартное состояние для серы: сера твердая в ромбической модификации. Далее: О2, SO2 – идеальные газы, реакция проводится при температуре Т, и общем давлении P0 = 1 атм. При невозможности осуществить реакцию образования экспериментально, Изменение стандартной энергии Гиббса в произвольной реакции (1) равно разности между суммой мольных энергий образования продуктов, умноженных на стехиометрические коэффициенты при соответствующих веществах и аналогичной суммой мольных энергий образования реагентов
Если в реакции принимают участие простые вещества, то при вычисления SО2 (г) + 1/2О2 (г) = SO3 (г) (13)
При этом Такое правило следует из закона Гесса, который справедлив для любых функций состояния, в том числе и для (1) S (тв, ромб.) + 3/2О2 (г) = SO3 (г), (2) SO2 (г) = S (тв, ромб.) + О2 (г). Складывая почленно реакции (1) и (2) получаем суммарную реакцию (13) и соответствующее правило вычисления По определению G0 = H0 – TS0 После дифференцирования dG0 = dH0 – TdS0 – S0dT При Т = const
и
В соответствие с уравнением (15) изменение стандартной энергии Гиббса можно вычислять по данным о стандартной энтальпии реакции Пример. Определить ∆G0 при 218,15 реакции (13) а) по Гиббсовым энергиям образования; б) по данным ∆H0 и ∆S0. Решение. Из справочных данных находим
∆G0 = -370,45 + 300,19 = - 70,26 кДж ∆H0 = -395,2 + 296,9 = -98,3 кДж
∆S0 = 256,65 – (248,11 + 1/2· 205,03) = -93,98 Дж·К-1 T∆S0 = -93,98·248,15 = -28,02 кДж ∆G0 = ∆H0 – T∆S0 = -70,3 кДж Комментарий. Поскольку известны абсолютные значения энтропии чистых веществ, ∆S0 вычисляют способом, который следует из физико-химического смысла стандартной реакции, как реакции между чистыми веществами.
По уравнению (15) вычисляют Пример. Рассчитать Решение. Реакция образования SO3 S (тв, ромб.) + 3/2О2 (г) = SO3 (г),
где
Из справочных данных имеем

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ,
,  ,
,  ,
,  . Вещества А, В, С, D по свойствам идеальные газы, их смесь – идеально-газовый раствор. Смесь находится при температуре Т и общем давлении Р, которые в дальнейшем поддерживаются постоянными. В данном состоянии возможна самопроизвольная реакция
. Вещества А, В, С, D по свойствам идеальные газы, их смесь – идеально-газовый раствор. Смесь находится при температуре Т и общем давлении Р, которые в дальнейшем поддерживаются постоянными. В данном состоянии возможна самопроизвольная реакция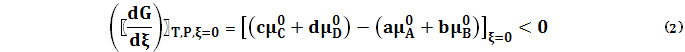
 ,
,  ,
,  ,
,  – химические потенциалы соответствующих веществ в исходном состоянии (ξ=0), состав которого задается количеством молей
– химические потенциалы соответствующих веществ в исходном состоянии (ξ=0), состав которого задается количеством молей  , i = А, В, С, D могут быть равны стехиометрическим коэффициентам или иметь иные значения.
, i = А, В, С, D могут быть равны стехиометрическим коэффициентам или иметь иные значения.





 значение производной
значение производной  для исходного состояния.
для исходного состояния.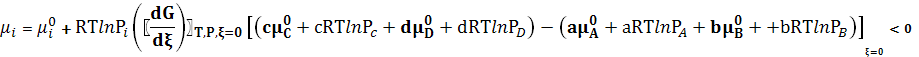
 – парциальные давления веществ А, В, С, D в исходном состоянии.
– парциальные давления веществ А, В, С, D в исходном состоянии.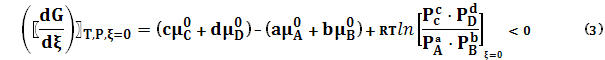
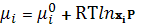
 +
+ 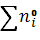
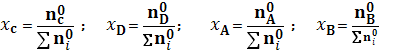


 ,
,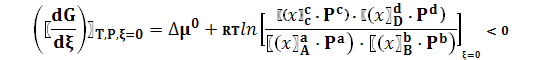

 по определению не зависит ни от состава системы, ни от давления и при данной Т остается постоянной, при изменении ξ от нуля до ξе в состоянии равновесия и от ξе до единицы на участке, где прямая реакция (1) невозможна, но возможен самопроизвольный процесс в обратном направлении
по определению не зависит ни от состава системы, ни от давления и при данной Т остается постоянной, при изменении ξ от нуля до ξе в состоянии равновесия и от ξе до единицы на участке, где прямая реакция (1) невозможна, но возможен самопроизвольный процесс в обратном направлении
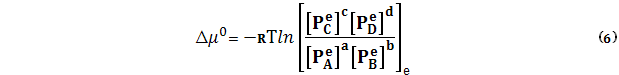
 также в состоянии равновесия будет равно
также в состоянии равновесия будет равно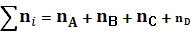
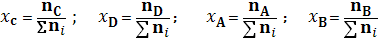
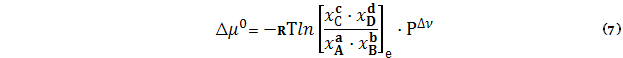
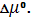
 – это химический потенциал одного моля чистого i–го идеального газа при данной температуре Т и стандартном давлении Р0 = 1 атм. Но для чистого вещества μ = g; μ0 = g0 и для
– это химический потенциал одного моля чистого i–го идеального газа при данной температуре Т и стандартном давлении Р0 = 1 атм. Но для чистого вещества μ = g; μ0 = g0 и для 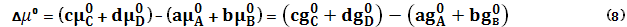
 – это энергия Гиббса
– это энергия Гиббса  чистого идеального газа С, количество молей которого равно с.
чистого идеального газа С, количество молей которого равно с.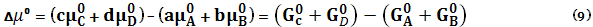
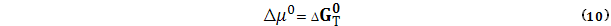
 называется изменением стандартной энергии Гиббса или сокращенно стандартной энергией Гиббса (при температуре Т).
называется изменением стандартной энергии Гиббса или сокращенно стандартной энергией Гиббса (при температуре Т). соответствует изменению энергии Гиббса в реакции со стехиометрическим уравнением
соответствует изменению энергии Гиббса в реакции со стехиометрическим уравнением T, P0
T, P0
 T, P0
T, P0
 T, P0
T, P0
 T, P0
T, P0

 + = +
+ = + 
 реакции по энтальпиям образования и энтальпиям сгорания.
реакции по энтальпиям образования и энтальпиям сгорания. . Но
. Но  .
. .
.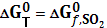


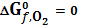 .
. . Покажем это на примере реакции (13), для которой закон Гесса в виде совокупности стадий выражается следующим образом:
. Покажем это на примере реакции (13), для которой закон Гесса в виде совокупности стадий выражается следующим образом: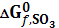

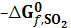
 веществ выпадают из итоговой величины и для них можно принять любое произвольное значение. По международным правилам принимается значение, равное нулю при любых температурах.
веществ выпадают из итоговой величины и для них можно принять любое произвольное значение. По международным правилам принимается значение, равное нулю при любых температурах.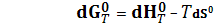
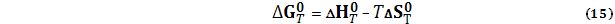
 и стандартной энтропии реакции
и стандартной энтропии реакции  .
. , кДж/моль
, кДж/моль
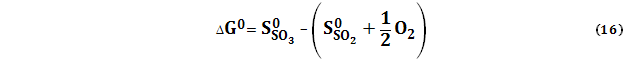
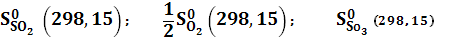
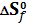 , вычисляемые через абсолютные значения чистых веществ
, вычисляемые через абсолютные значения чистых веществ  .
. при 298,15К, если
при 298,15К, если  = -395,2 кДж/моль.
= -395,2 кДж/моль.
 – изменение энтропии в реакции образования, которое находят по уравнению
– изменение энтропии в реакции образования, которое находят по уравнению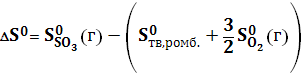

 256,68 – (31,80+3/2·205,03) = – 82,67 Дж/моль·К
256,68 – (31,80+3/2·205,03) = – 82,67 Дж/моль·К – 395,2 + 298,15·82,67 = – 370,45 кДж/моль
– 395,2 + 298,15·82,67 = – 370,45 кДж/моль