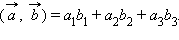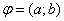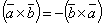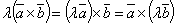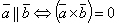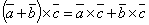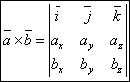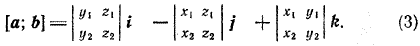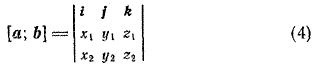|
|
Проекция ( геометрическая , алгебраическая) вектора на ось. Свойства проекций.Ответ:
Свойства проекций: Свойства проекции вектора Свойство 1. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: Это свойство позволяет заменять проекцию суммы векторов суммой их проекций и наоборот.
Свойство 2. Если вектор умножается на число λ, то его проекция на ось также умножается на это число:
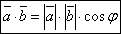
Свойство 3. Проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:
Орт оси. Разложение вектора по координатным ортам. Координаты вектора. Свойства координат Ответ: Орты осей.
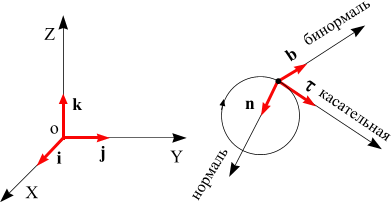
Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. В трёхмерном случае орты обычно обозначаются
При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:
Разложение вектора по координатным ортам. Орт координатной оси
Для любого вектора Если вектор
Координаты вектора: Чтобы вычислить координаты вектора , зная координаты (x1; y1) его начала A и координаты (x2; y2) его конца B, нужно из координат конца вычесть координаты начала: (x2 – x1; y2 – y1). Свойства координат. Рассмотрим координатную прямую с началом координат в точке О и единичным вектором i. Тогда для любого вектора a на этой прямой: a = axi. Число ax называется координатой вектора a на координатной оси. Свойство 1.При сложении векторов на оси их координаты складываются. Свойство 2.При умножении вектора на число его координата умножается на это число. Скалярное произведение векторов. Свойства. Ответ: Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.
Свойства: 1. Скалярное произведение обладает переместительным свойством: ab=bа
Скалярное произведение координатных ортов. Определение скалярного произведения векторов, заданных своими координатами. Ответ: Скалярное произведение (×) орты
Определение скалярного произведения векторов , заданных своими координатами. Скалярное произведение двух векторов
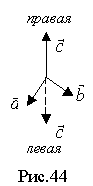
Векторное произведение двух векторов. Свойства векторного произведения. Ответ: Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую., если нет то в противоположном ( показать как он показывал с «ручками»)
Векторным произведением вектора ана векторbназывается вектор с который : 1. Перпендикулярен векторам а иb 2. Имеет длину, численно равную площади параллелограмма, образованного на a и bвекторах
3. Векторы, a ,b, и c образуют правую тройку векторов Свойства: 1. 2. 3. 4.
Векторное произведение координатных ортов. Определение векторного произведения векторов, заданных своими координатами. Ответ: Векторное произведение координатных ортов.
Определение векторного произведения векторов, заданных своими координатами. Пусть векторы а = (х1; у1; z1) и b = (х2; у2; z2) заданы своими координатами в прямоугольной декартовой системе координат О, i, j, k, причем тройка i, j, k является правой. Разложим а и b по базисным векторам: а = x1i + y1 j + z1 k, b = x2 i + y2 j + z2 k. Используя свойства векторного произведения, получаем [а; b] = [x1 i + y1 j + z1 k ; x2 i + y2 j + z2 k] = = x 1x2 [i; i] + x1 y2 [i; j] + x1 z2 [i; k] + + y1 x2 [j; i] + y1 y2 [j; j] + y1 z2 [j; k] + + z1 x2 [k; i] + z1 y2 [k; j] + z1 z2 [k; k]. (1) По определению векторного произведения находим [i; i] = 0, [i; j] = k, [i; k]= — j, [j; i] = — k, [j; j] = 0, [j; k] = i, [k; i] = j, [k; j] = — i. [k; k] = 0. Учитывая эти равенства, формулу (1) можно записать так: [а; b] = x1 y2 k — x1 z2 j — y1 x2 k + y1 z2 i + z1 x2 j — z1 y2 i Или [а; b] = (y1 z2 — z1 y2) i + (z1 x2 — x1 z2 ) j + (x1 y2 — y1 x2) k. (2) Формула (2) дает выражение для векторного произведения двух векторов, заданных своими координатами. Полученная формула громоздка .Используя обозначения определителей можно записать ее в другом более удобном для запоминания виде:
Обычно формулу (З) записывают еще короче:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

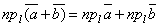
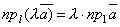
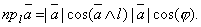

 и
и  Могут также применяться обозначения со стрелками
Могут также применяться обозначения со стрелками 
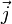 и
и 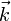
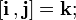
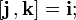
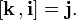
 обозначается через
обозначается через  , оси
, оси  - через
- через  , оси
, оси  - через
- через 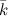 (рис. 1)
(рис. 1)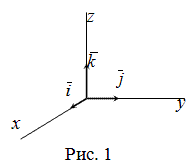
 который лежит в плоскости
который лежит в плоскости  имеет место следующее разложение:
имеет место следующее разложение: 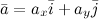
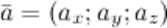 расположен в пространстве, то разложение по ортам координатных осей имеет вид:
расположен в пространстве, то разложение по ортам координатных осей имеет вид: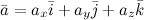
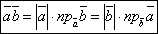
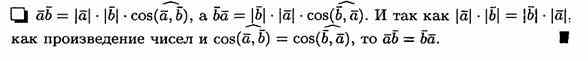


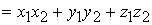
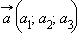 и
и  заданных своими координатами, может быть вычислено по формуле
заданных своими координатами, может быть вычислено по формуле