
|
|
Расчет режимов простых замкнутых сетей2.2.1. Правило моментов
Простые замкнутые сети содержат один контур, образованный элементами сети. Основополагающей формулой для расчета режимов таких сетей является правило моментов:
где Формула (2.1) справедлива для контура с числом нагрузок n и числом участков (обычно линий) n+1. Пример замкнутого контура с тремя линиями и двумя нагрузками показан на рис. 2.6 и 2.7. Для такого контура правило моментов принимает вид
Если отношение индуктивного сопротивления к активному на всех участках замкнутой сети одинаково, то такая сеть называется однородной. Так как полные сопротивления в этом случае прямо пропорциональны активным сопротивлениям, то для однородной сети правило моментов можно записать в следующем виде:
где сопряженные комплексы полных сопротивлений заменены аналогичными активными сопротивлениями. В частности, условие однородности выполняется для сети, у которой все линии выполнены проводами одного сечения с одинаковым расположением на опорах и одинаковым числом цепей. При этом сопротивления пропорциональны длинам линий. Следовательно, для такой сети правило моментов примет вид
где liS – суммарная длина линий от i-й нагрузки до противоположного источника питания; lS – суммарная длина линий между источниками питания. В однородных сетях распределения активной и реактивной мощности в сети независимы друг от друга. Поэтому правило моментов можно записать отдельно для активной и реактивной мощности:
2.2.2. Расчет кольцевых сетей
Режим кольцевой сети рассчитывается в следующем порядке. 1. Рассчитывается потокораспределение без учета потерь мощности. Мощности на головных участках вычисляются по правилу моментов, а на остальных участках – по первому закону Кирхгофа. 2. Определяются положения точек потокораздела по активной и реактивной мощности – узлов сети, при переходе через которые соответствующая мощность меняет направление. 3. Контур разделяется на эквивалентные разомкнутые сети. Если точки потокораздела по активной и реактивной мощности находятся в одном и том же узле, то этот узел является точкой разделения сети, которое производится таким образом, чтобы потокораспределение осталось прежним. Если точки потокораздела по активной и реактивной мощности не совпадают, то участок между точками потокораздела вырезается, а нагрузки корректируются таким образом, чтобы потокораспределение в целом не изменилось, но были бы учтены потери мощности на вырезанном участке. 4. Производится окончательный расчет потокораспределения в эквивалентных разомкнутых сетях с учетом потерь мощности методом «по данным начала»; 5. Вычисляются напряжения в узлах сети методом «по данным начала».
2.2.3. Расчет сетей с двухсторонним питанием
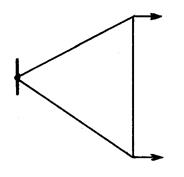
Для расчета таких сетей обычно используют метод наложения. При этом рассматривается два частичных режима: 1. Напряжения источников питания принимаются одинаковыми, а расчетные нагрузки подстанций – фактическими. В данном режиме сеть эквивалентна кольцевой. 2. Напряжения источников принимаются фактическими, а расчетные нагрузки подстанций – равными нулю. Определяется уравнительная мощность, обусловленная разницей напряжений источников питания (рис. 2.8). Результаты расчета потокораспределения в частичных режимах суммируются (с учетом направлений). После этого вычисляются напряжения в узлах сети.
Рис. 2.8.К расчету уравнительной мощности Уравнительнаямощность может быть определена либо через ток и номинальное напряжение, либо как среднее от мощности, выдаваемой первым источником, и мощности, потребляемой вторым источником. В последнем случае расчетная формула имеет вид:
где δ1, δ2 – фазы напряжений 2.2.4. Задачи Задача 1 Рассчитать режим кольцевой сети с тремя линиями. Варианты исходных данных:
Рассчитать режим сети с двухсторонним питанием, если Задача 3

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (2.1)
, (2.1) – мощность головного участка (то есть участка, соединенного с источником питания); n – число нагрузок (подстанций);
– мощность головного участка (то есть участка, соединенного с источником питания); n – число нагрузок (подстанций);  – расчетная нагрузка i-й подстанции;
– расчетная нагрузка i-й подстанции; 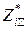 – сопряженный комплекс суммарного сопротивления от i-й нагрузки до противоположного данному головному участку источника питания;
– сопряженный комплекс суммарного сопротивления от i-й нагрузки до противоположного данному головному участку источника питания;  – сопряженный комплекс суммарного сопротивления между источниками питания.
– сопряженный комплекс суммарного сопротивления между источниками питания. .
.

 , (2.2)
, (2.2) , (2.3)
, (2.3)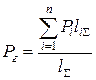 , (2.4)
, (2.4)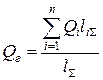 . (2.5)
. (2.5)
 ,(2.6)
,(2.6) ,
, 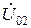 .
.





 1. U0 = 115 кВ. Расчетные нагрузки подстанций
1. U0 = 115 кВ. Расчетные нагрузки подстанций  МВА,
МВА,  МВА. Длины и погонные параметры линий l1 = 30 км, l2 = 40 км, l3 = 50 км, r0,1 = r0,2 = r0,3 = 0,25 Ом/км, x0,1 = x0,2 = x0,3 = 0,42 Ом/км, b0,1 = b0,2 = b0,3 = 2,7 мкСм/км. Линии одноцепные.
МВА. Длины и погонные параметры линий l1 = 30 км, l2 = 40 км, l3 = 50 км, r0,1 = r0,2 = r0,3 = 0,25 Ом/км, x0,1 = x0,2 = x0,3 = 0,42 Ом/км, b0,1 = b0,2 = b0,3 = 2,7 мкСм/км. Линии одноцепные.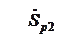

 2. U1 = 220 кВ,
2. U1 = 220 кВ, 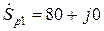 МВА,
МВА,  МВА. Параметры схем замещения линий Zл1 = 8 + j34 Ом, Zл2 = 5 + j21 Ом, Zл3 = 7 + j31 Ом, Bл1 = 210 мкСм, Bл3 = 196 мкСм.
МВА. Параметры схем замещения линий Zл1 = 8 + j34 Ом, Zл2 = 5 + j21 Ом, Zл3 = 7 + j31 Ом, Bл1 = 210 мкСм, Bл3 = 196 мкСм.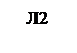



 Задача 2
Задача 2 МВА, U0,1 = 115 кВ, U0,2 = 112 кВ, фазы напряжений источников одинаковы. Длины и погонные параметры линий l1 = 50 км, l2 = 40 км, r0,1 = 0,42 Ом/км, r0,2 = 0,3 Ом/км, x0,1 = 0,44 Ом/км, x0,2 = 0,43 Ом/км, b0,1 = 2,57 мкСм/км, b0,2 = 2,64 мкСм/км. Линии одноцепные.
МВА, U0,1 = 115 кВ, U0,2 = 112 кВ, фазы напряжений источников одинаковы. Длины и погонные параметры линий l1 = 50 км, l2 = 40 км, r0,1 = 0,42 Ом/км, r0,2 = 0,3 Ом/км, x0,1 = 0,44 Ом/км, x0,2 = 0,43 Ом/км, b0,1 = 2,57 мкСм/км, b0,2 = 2,64 мкСм/км. Линии одноцепные.

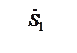







 Рассчитать режим сложнозамкнутой сети, если
Рассчитать режим сложнозамкнутой сети, если  МВА,
МВА,  МВА, U0 = 115 кВ. Погонные активные сопротивления, индуктивные сопротивления и зарядные мощности для всех линий одинаковы и равны r0 = x0 = = 0,43 Ом/км, q0 = 0,034 Мвар/км. Длины линий l1 = l4 = l5 = 30 км, l2 = l3 = 40 км. Все линии одноцепные.
МВА, U0 = 115 кВ. Погонные активные сопротивления, индуктивные сопротивления и зарядные мощности для всех линий одинаковы и равны r0 = x0 = = 0,43 Ом/км, q0 = 0,034 Мвар/км. Длины линий l1 = l4 = l5 = 30 км, l2 = l3 = 40 км. Все линии одноцепные.