Линейное приближение экспериментальных данных
Экспериментально получены пять значений функции  при пяти значениях аргумента при пяти значениях аргумента  , которые представлены в данной таблице. Методом наименьших квадратов найти функцию , которые представлены в данной таблице. Методом наименьших квадратов найти функцию  , описывающую приближенно (аппроксимирующую) экспериментальные данные. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки , описывающую приближенно (аппроксимирующую) экспериментальные данные. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки  и график аппроксимирующей функции и график аппроксимирующей функции  . .
Решение. Из условия задачи имеем:
 - это значения переменной - это значения переменной  , полученные экспериментально. , полученные экспериментально.
 -это значения переменной -это значения переменной  , рассчитанные теоретически по формуле , рассчитанные теоретически по формуле  . Вычислим разность между экспериментальными и теоретическими значениями переменной . Вычислим разность между экспериментальными и теоретическими значениями переменной  , т.е. , т.е.  . Эта разность может быть как положительной, так и отрицательной. Мы будем рассматривать эту разность в квадрате, т.е. . Эта разность может быть как положительной, так и отрицательной. Мы будем рассматривать эту разность в квадрате, т.е.  . Просуммируем эти квадраты разностей по всем . Просуммируем эти квадраты разностей по всем 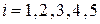 : :  . Наилучшими значениями параметров . Наилучшими значениями параметров 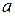 и и  будем считать те, при которых сумма будем считать те, при которых сумма  принимает минимальное значение. принимает минимальное значение.
Таким образом, получаем классическую задачу: найти точку минимума функции двух переменных  . По теории минимум функция . По теории минимум функция  может принимать только в тех точках, в которых частные производные может принимать только в тех точках, в которых частные производные  и и  . Вычисления приведут к системе . Вычисления приведут к системе
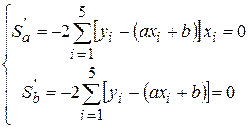
Учитывая, что неизвестными в этих уравнениях являются параметры 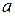 и и  , преобразуем систему к шаблонному виду, удобному для использования формул Крамера. , преобразуем систему к шаблонному виду, удобному для использования формул Крамера.
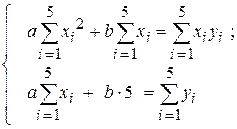
 Тогда: Тогда:  ; ;  . .
Значения сумм приведены в таблице
| i
| xi
| yi
| xi^2
| xi yi
| |
|
| 4,3
|
| 4,3
| |
|
| 5,3
|
| 10,6
| |
|
| 3,8
|
| 11,4
| |
|
| 1,8
|
| 7,2
| |
|
| 2,3
|
| 11,5
| | Сумма
|
| 17,5
|
|
|
Вычислим:
 ; ; 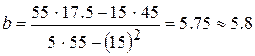
Линейная функция 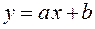 , описывающая приближенно экспериментальные данные, имеет вид , описывающая приближенно экспериментальные данные, имеет вид  . Ее график, а также экспериментальные значения . Ее график, а также экспериментальные значения  изображены на рис. 2. изображены на рис. 2.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ «ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ»
| Задача № 1.Установить, удовлетворяет ли данная функция данному дифференциальному уравнению в частных производных
| | 1.
| 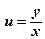 ; ;

| 8.
|  ; ;

| | 2.
|  ; ;

| 9.
|  ; ;

| | 3.
|  ; ;
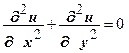
| 10.
|  ; ;

| | 4.
|  ; ;
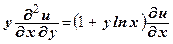
| 11.
|  ; ;

| | 5.
| 

| 12.
|  ; ;

| | 6.
| 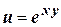 
| 13.
|  
| | 7.
|  
| 14.
| 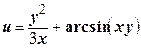 ; ; 
|
Задача № 2Найти уравнение касательной плоскости к поверхности  в точке в точке 
| | 1.
|  ; ;

| 8.
|  ; ;

| | 2.
|  ; ;
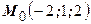
| 9.
|  ; ;

| | 3.
| 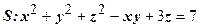 ; ;

| 10.
|  ; ;

| | 4.
|  ; ;

| 11.
|  ; ;
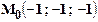
| | 5.
|  ; ;

| 12.
|  ; ;

| | 6.
|  ; ;

| 13.
|  ; ;

| | 7.
|  ; ;

| 14.
|  ; ;

|
| Задача № 3Найти область определения функции
| | 1.
| 
| 8.
| 
| | 2.
| 
| 9.
| 
| | 3.
| 
| 10.
| 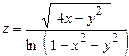
| | 4.
| 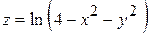
| 11.
| 
| | 5.
| 
| 12.
| 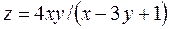
| | 6.
| 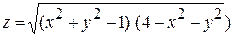
| 13.
| 
| | 7.
| 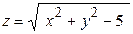
| 14.
| 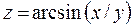
|
| Задача № 4Исследовать на экстремум функцию
| | 1.
| 
| 8.
| 
| | 2.
| 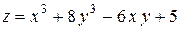
| 9.
| 
| | 3.
| 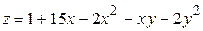
| 10.
| 
| | 4.
| 
| 11.
| 
| | 5.
| 
| 12.
| 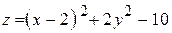
| | 6.
| 
| 13.
| 
| | 7.
| 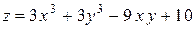
| 14.
| 
| | Задача № 5Найти производную данной функции в данной точке в направлении заданного вектора
| | 1.
| 
 ; ; 
| 8.
| 
 ; ; 
| | 2.
| 
 ; ; 
| 9.
| 
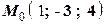 ; ; 
| | 3.
| 
 ; ; 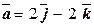
| 10.
| 
 в направлении вектора в направлении вектора  , где точка , где точка  . .
| | 4.
| 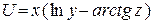
 ; ; 
| 11.
| 
 ; ; 
| | 5.
| 
 ; ; 
| 12.
|  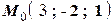 ; ; 
| | 6.
| 
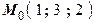 ; ; 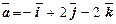
| 13.
| 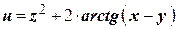
 ; ; 
| | 7.
| 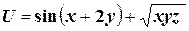 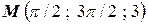 ; ; 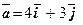
| 14.
| 
 ; ; 
| | | | | | | | |
| Задача № 6Вычислить приближённо с помощью полного дифференциала значение выражения
| | 1.
| 
| 8.
| 
| | 2.
| 
| 9.
| 
| | 3.
| 
| 10.
| 
| | 4.
| 
| 11.
| 
| | 5.
| 
| 12.
|  при при 
| | 6.
| 
| 13.
|  при при 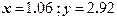
| | 7.
| 
| 14.
|  при при 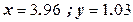
|
Задача № 7Найти наименьшее и наибольшее значения функции на замкнутой области  : :
| | 1.
|  ; ;

| 8.
|  ; ;

| | 2.
| 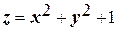 ; ; 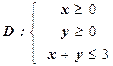
| 9.
| 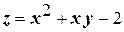 ; ;

| | 3.
|  ; ;

| 10.
|  ; ;

| | 4.
|  ; ;

| 11.
| 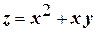 ; ; 
| | 5.
|  
| 12.
|  ; ; 
| | 6.
|  
| 13.
|  ; ; 
| | 7.
|  ; ;

| 14.
|  ; ; 
| Список литературы
1. Данко, П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для студентов втузов: в 2 т./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. школа, 1980. – Т.1. – 320 с.
2. Сборник индивидуальных заданий по высшей математике: учеб. пособие для инжер.-техн. специальностей вузов: в 3 ч. / под общ. ред. А.П. Рябушко. Ч. 2. – Минск: Академ. книга, 2006. – 351 с.: ил.
31.
Содержание
Введение............................................................................................................... 3
§1. Функции двух и трех переменных ................................................................ 3
1.1 Частные производные функции двух и трех переменных................... 3
§2. Приложения частных производных............................................................... 8
2.1. Производная по направлению функции двух и трех переменных..... 8
2.2. Полный дифференциал функции двух и трех переменных.
Линеаризация функции двух и трех переменных. Использование
полного дифференциала в приближенных вычислениях................... 11
2.3. Экстремумы функции двух переменных............................................ 14
2.4. Условный экстремум функции двух переменных............................... 15
2.5. Наибольшее и наименьшее значения функции двух переменных
на замкнутой области......................................................................... 15
§3. Линейное приближение экспериментальных данных.................................. 18
Задачи для контрольной работы «Функции двух и трех переменных»........... 20
Литература.......................................................................................................... 24
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 при пяти значениях аргумента
при пяти значениях аргумента  , которые представлены в данной таблице. Методом наименьших квадратов найти функцию
, которые представлены в данной таблице. Методом наименьших квадратов найти функцию  , описывающую приближенно (аппроксимирующую) экспериментальные данные. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки
, описывающую приближенно (аппроксимирующую) экспериментальные данные. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки  и график аппроксимирующей функции
и график аппроксимирующей функции  - это значения переменной
- это значения переменной  , полученные экспериментально.
, полученные экспериментально. -это значения переменной
-это значения переменной  . Вычислим разность между экспериментальными и теоретическими значениями переменной
. Вычислим разность между экспериментальными и теоретическими значениями переменной  . Эта разность может быть как положительной, так и отрицательной. Мы будем рассматривать эту разность в квадрате, т.е.
. Эта разность может быть как положительной, так и отрицательной. Мы будем рассматривать эту разность в квадрате, т.е.  . Просуммируем эти квадраты разностей по всем
. Просуммируем эти квадраты разностей по всем 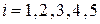 :
:  . Наилучшими значениями параметров
. Наилучшими значениями параметров 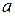 и
и  будем считать те, при которых сумма
будем считать те, при которых сумма  принимает минимальное значение.
принимает минимальное значение. и
и  . Вычисления приведут к системе
. Вычисления приведут к системе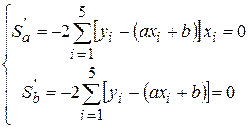
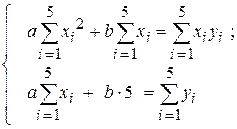
 Тогда:
Тогда:  ;
;  .
. ;
; 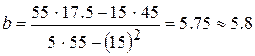
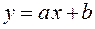 , описывающая приближенно экспериментальные данные, имеет вид
, описывающая приближенно экспериментальные данные, имеет вид  . Ее график, а также экспериментальные значения
. Ее график, а также экспериментальные значения  изображены на рис. 2.
изображены на рис. 2.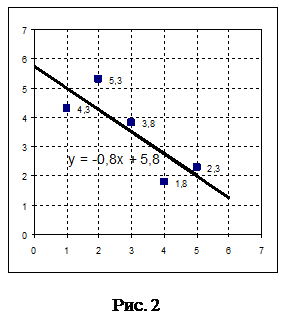
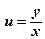 ;
;

 ;
;

 ;
;

 ;
;

 ;
;
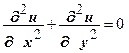
 ;
;

 ;
;
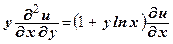
 ;
;



 ;
;

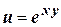





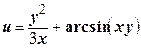 ;
; 
 в точке
в точке 
 ;
;

 ;
;

 ;
;
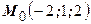
 ;
;

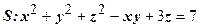 ;
;

 ;
;

 ;
;

 ;
;
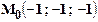
 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;






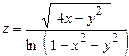
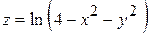


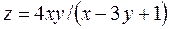
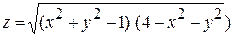

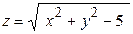
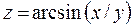


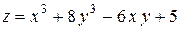

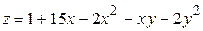




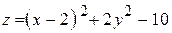


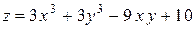


 ;
; 

 ;
; 

 ;
; 

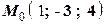 ;
; 

 ;
; 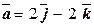

 в направлении вектора
в направлении вектора  , где точка
, где точка  .
.
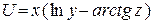
 ;
; 

 ;
; 

 ;
; 

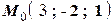 ;
; 

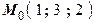 ;
; 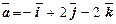
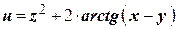
 ;
; 
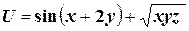
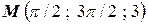 ;
; 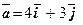

 ;
; 









 при
при 

 при
при 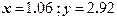

 при
при 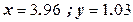
 :
:
 ;
;

 ;
;

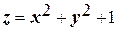 ;
; 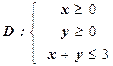
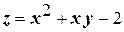 ;
;

 ;
;

 ;
;

 ;
;

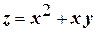 ;
; 


 ;
; 


 ;
; 
 ;
;

 ;
; 